在统计学中,自由度(degree of freedom, df)指的是计算某一统计量时,取值不受限制的变量个数。通常df=n-k。其中n为样本数量,k为被限制的条件数或变量个数,或计算某一统计量时用到其它独立统计量的个数。自由度通常用于抽样分布中。
2018.11.16
1、生成式模型(Generative Model)与判别式模型(Discrimitive Model)是分类器常遇到的概念,它们的区别在于:(对于输入x,类别标签y)
- 1. 生成式模型估计它们的联合概率分布P(x,y)
- 2. 判别式模型估计决策函数F(X)或条件概率分布P(y|x)
- 3. 生成式式模型可以根据贝叶斯公式得到判别式模型,但反过来不行
## 生成式模型
- 1. 判别式分析
- 2. 朴素贝叶斯Native Bayes
- 3. 混合高斯型Gaussians
- 4. K近邻KNN
- 5. 隐马尔科夫模型HMM
- 6. 贝叶斯网络
- 7. sigmoid belief networks
- 8. 马尔科夫随机场Markov random fields
- 9. 深度信念网络DBN
- 10. 隐含狄利克雷分布简称LDA(Latent Dirichlet allocation)
- 11. 多专家模型(the mixture of experts model)
## 判别式模型
- 1. 线性回归linear regression
- 2. 逻辑回归logic regression
- 3. 神经网络NN
- 4. 支持向量机SVM
- 5. 高斯过程Gaussian process
- 6. 条件随机场CRF
- 7. CART(Classification and regression tree)
- 8. Boosting
2018.10.27
- AR模型:自回归模型,是一种线性模型
- MA模型:移动平均法模型,其中使用趋势移动平均法建立直线趋势的预测模型
- ARMA模型:自回归滑动平均模型,拟合较高阶模型
- GARCH模型:广义回归模型,对误差的方差建模,适用于波动性的分析和预测
2018.10.17
- EM算法: 只有观测序列,无状态序列时来学习模型参数,即Baum-Welch算法
- 维特比算法: 用动态规划解决HMM的预测问题,不是参数估计
- 前向后向:用来算概率
- 极大似然估计:即观测序列和相应的状态序列都存在时的监督学习算法,用来估计参数
2018.10.7
1、Floyd算法用于求最短路径。Floyd算法可以说是Warshall算法的扩展,三个for循环就可以解决问题,所以它的时间复杂度为O(n^3)。
Floyd算法的基本思想如下:从任意节点A到任意节点B的最短路径不外乎2种可能,1是直接从A到B,2是从A经过若干个节点X到B。所以,我们假设Dis(AB)为节点A到节点B的最短路径的距离,对于每一个节点X,我们检查Dis(AX) + Dis(XB) < Dis(AB)是否成立,如果成立,证明从A到X再到B的路径比A直接到B的路径短,我们便设置Dis(AB) = Dis(AX) + Dis(XB),这样一来,当我们遍历完所有节点X,Dis(AB)中记录的便是A到B的最短路径的距离。代码看起来可能像下面这样:
int n;//n为节点个数 for(int i=0; i<n; ++i ) { for (int j=0; j<n; ++j ) { for ( int k=0; k<n; ++k ) { if ( Dis[i][k] + Dis[k][j] < Dis[i][j] ) { // 找到更短路径 Dis[i][j] = Dis[i][k] + Dis[k][j]; } } } }

2、链表不能随机访问,只能顺序存储,因此不能用二分查找,只能从头到尾依次查找,以链接方式存储的线性表(X1、X2、...、Xn),当访问第i个元素的时间复杂度为O(n)。
十字链表(Orthogonal List)是有向图的另一种 链式存储结构 。该结构可以看成是将有向图的 邻接表 和逆邻接表结合起来得到的。用十字链表来存储有向图,可以达到高效的存取效果。同时,代码的可读性也会得到提升。
无向图的存储结构包括邻接矩阵,邻接数组和邻接表。
3、数值概率算法(数值问题的求解,最优化问题的近似解)、蒙特罗卡算法(判定问题的准确解,不一定正确)、拉斯维加斯算法(不一定会得到解,但得到的解一定是正确解)、舍伍德算法(总能求得一个解,且一定是正确解)。
算法分析的两个主要方面就是分析算法的时间复杂度和空间复杂度,以考察算法的时间和空间效率。
4、在AOE网中,从源点到汇点的所有路径中,具有最大路径长度的路径成为关键路径。在AOE网中,可以有不止一条的关键路径。
5、当一棵具有n个叶结点的二叉树的WPL值为最小时,称其树为哈夫曼树。 哈夫曼树的形态不是唯一的,但是它的带权路径长度WPL是唯一的。二叉树中节点的左右子树是有序的。当根据n个叶结点的二叉树的WPL值最小构造树时,如果兄弟结点的权值相等,形状就不唯一了。权值较大的关键字离根近的话,乘的系数就相应的小,路径长度就小。
在哈夫曼树中,左右孩子权值之和为父结点权值。若两个10分别属于两棵不同的子树,根的权值不等于其孩子的权值和;若两个10属同棵子树,其权值不等于其两个孩子(叶结点)的权值和。
6、Hadoop的三种运行模式 :
2.伪分布式模式: Hadoop守护进程运行在本地机器上,模拟一个小规模的集群,换句话说,可以配置一台机器的Hadoop集群,伪分布式是完全分布式的一个特例。
3.完全分布式模式:Hadoop守护进程运行在一个集群上。
注意:所谓分布式要启动守护进程 ,即:使用分布式hadoop时,要先启动一些准备程序进程,然后才能使用比如start-dfs.sh start-yarn.sh。而本地模式不需要启动这些守护进程
7、满足下面两个条件的问题就是NPC问题。首先,它得是一个NP问题;然后,所有的NP问题都可以约化到它。
- P: 能在多项式时间内解决的问题
- NP: 不能在多项式时间内解决或不确定能不能在多项式时间内解决,但 能在多项式时间验证的问题
- NPC: NP完全问题, 所有NP问题在多项式时间内都能约化(Reducibility)到它的NP问题 ,即解决了此NPC问题,所有NP问题也都得到解决。
- NP hard:NP难问题, 所有NP问题在多项式时间内都能约化(Reducibility)到它的问题(不一定是NP问题)。
8、线性结构是一个有序数据元素的集合。常用的线性结构有:线性表,栈,队列,双队列,数组,串。
- 1.集合中必存在唯一的一个"第一个元素";
- 2.集合中必存在唯一的一个"最后的元素";
- 3.除最后元素之外,其它数据元素均有唯一的"后继";
- 4.除第一元素之外,其它数据元素均有唯一的"前驱"。
2018.9.28
1、均值偏移(mean shift,也叫均值漂移或均值平移)这个概念最早是由Fukunaga等人于1975年在《The estimation of the gradient of a density function with application in pattern recognitioin》这篇关于概率密度梯度函数的估计中提出来的,其最初含义就是偏移的均值向量。它沿着概率梯度的上升方向寻找分布的峰值,是一种在一组数据的密度分布中寻找局部极值的稳定的无参特征空间估计方法(non-parametric feature-space analysis)。“稳定”是指统计意义上的稳定,因为mean-shift忽略了数据中的outlier,即忽略原理数据峰值的点。mean-shift只对数据局部窗口中的点进行处理,处理完成后再移动窗口。

MeanShift算法通过迭代运算收敛于概率密度函数的局部最大值,实现目标定位和跟踪,也能对可变形状目标实时跟踪,对目标的变形,旋转等运动也有较强的鲁棒性。MeanShift算法是一种自动迭代跟踪算法,由 MeanShift补偿向量不断沿着密度函数的梯度方向移动。在一定条件下,MeanShift算法能收敛到局部最优点,从而实现对运动体准确地定位。
在Mean Shift算法中引入核函数的目的是使得随着样本与被偏移点的距离不同,其偏移量对均值偏移向量的贡献也不同。在Mean Shift算法中,最关键的就是计算每个点的偏移均值,然后根据新计算的偏移均值更新点的位置。
(https://blog.csdn.net/ncut_matlab/article/details/50581726)Mean Shift算法的缺陷:
- calculation intensive,一般需要的计算复杂度(主要用于计算欧式距离),为样本数,为每个数据点的平均迭代次数。
- Rely on sufficient high data density with clear gradient to locate the cluster centers。因而其对一些data outliers 无法找到合适的聚类。即一些小的不确定的聚类。
2018.9.25
1、队列可用链表来实现,实现也很简单。但是队列也可用数组来实现,使用循环数组比链表有更高的效率。由于循环数组的特殊性,一个循环数组中必须空出一个位置,不然无法判断队列是否为空或者为满的。
循环数组来实现队列的难点便在索引的值,我们要把数组当做一个圆来看,当索引来到数组的0或者最后一个位置时,必须能够得到正确的索引。
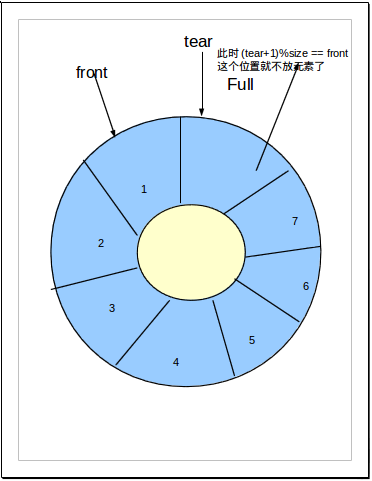
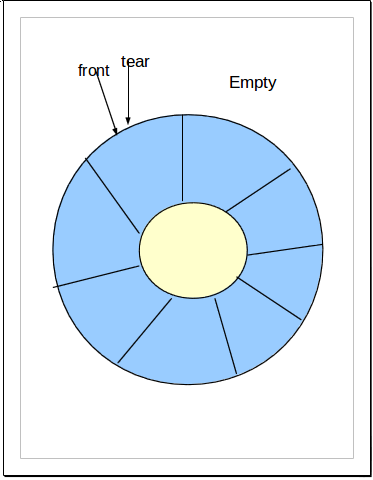
为充分利用向量空间,克服”假溢出”现象的方法是:将向量空间想象为一个首尾相接的圆环,并称这种向量为循环向量。存储在其中的队列称为循环队列(Circular Queue)。这种循环队列可以以单链表的方式来在实际编程应用中来实现。
循环队列中,由于入队时尾指针向前追赶头指针;出队时头指针向前追赶尾指针,造成队空和队满时头尾指针均相等。因此,无法通过条件front==rear来判别队列是”空”还是”满”。解决这个问题的方法至少有两种:
1). 另设一布尔变量以区别队列的空和满;
2). 另一种方式就是数据结构常用的: 队满时:(rear+1)%n==front,n为队列长度(所用数组大小),由于rear,front均为所用空间的指针,循环只是逻辑上的循环,所以需要求余运算。
front指定队首位置,删除一个元素就将front顺时针移动一位,每删除一个元素就加1。
rear指向元素要插入的位置,插入一个元素就将rear顺时针移动一位,后方每插入一个元素就加1。

2、判定一个有向图上是否存在回路除了可以利用拓扑排序方法外,还可以用深度优先遍历方法。深度优先遍历是先在一条路径走到叶节点后回溯,然后继续遍历。
如果W是由有序树V转换的二叉树,则V中的结点的后序遍历顺序是W结点的中序遍历。
3、数据库性能用开销( cost ),即时间、空间及可能的费用来衡量,则在数据库应用系统生命周期中总的开销包括规划开销、设计开销、实施和测试开销、操作开销和运行维护开销。对物理设计来说,主要考虑操作开销,即为使用户获得及时、准确的数据所需的开销和计算机资源的开销。
4、用parzen窗法估计类概率密度函数时,窗宽过窄导致波动过大的原因是:a)窗函数幅度过大;b)窗口中落入的样本数过少。
Parzen窗估计属于非参数估计。所谓非参数估计是指,已知样本所属的类别,但未知总体概率密度函数的形式,要求我们直接推断概率密度函数本身。非参数估计的方法主要有:直方图法、核方法。Parzen窗估计属于核方法的一种。Parzen窗法是另外一种在取值空间中进行取样估计的方法,或者说可以看作是用核函数对样本在取值空间中进行插值。Parzen窗估计方法的主题思想是固定窗口区域容积,去看有多少个样本点在里面。
核密度估计是在概率中用来估计未知的密度函数,又名Parzen窗(Parzen window),由Rosenblatt (1955)和Emanuel Parzen(1962)提出,基本思想是利用一定范围内各点密度的平均值对总体密度函数进行估计。
5、决策树学习算法主要有:ID3算法、C4.5算法和CART算法。
MD5英文全称是Message Digest Algorithm(信息摘要算法),是计算机安全领域广泛应用的一个压缩加密的哈希算法。
ID3算法是有Quinlan首先提出的,该算法是以信息论为基础,以信息熵和信息增益度为衡量标准,从而实现对数据的归纳分类。ID3算法要求特征必须离散化;信息增益可以用熵,而不是GINI系数来计算;选取信息增益最大特征,作为树的根节点。
ID3算法是决策树学习算法的一种,决策树学习是一种逼近离散值目标函数的方法,学习得到的决策树可以被表示为多个if-then规则,故ID3算法并不是二叉树模型。
基本的ID3算法通过自顶向下构造决策树来进行学习,一般选择分类能力最好的属性来作为树的根节点,具有最高信息增益的属性认为是最好的属性。
信息增益可以通过熵来计算,我们用训练样例的熵来刻画任意样例集的纯度,简单地说,一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低。信息增益是ID3算法增长树的每一步中选取最佳属性的度量标准。
6、关键词选取的方法主要有两种:无监督的方法,利用候选关键词的统计性质,对他们排序,选取最高的若干个作为关键词;有监督的方法,将关键词抽取问题转换为判断每个候选关键词是否为关键词的二分类问题,他需要一个已经标注关键词的文档集合训练分类模型。
多标签分类方法是关键词分配的方法。
基于标注图的方法和基于内容的方法是社会标签推荐的方法。
7、分词方法大致可分为三大类:基于字符串匹配的分词方法(机械分词方法)、基于统计的分词方法和基于理解的分词方法。
机械分词方法主要有整箱最大匹配算法、逆向最大匹配算法、双向最大匹配算法和最少切分算法。
8、主动学习方法:有时候,有类标号的数据比较稀少而没有类标号的数据相当丰富,但是对数据进行人工标注有非常安规,此时学习算法可以主动地提出一些标注请求,将一些经过筛选的数据提交给专家进行标注。
故主动学习并不属于监督学习、无监督学习和半监督学习的范畴,因为主动学习过程中指的是主动提出标注请求,也就是需要一个外在的能够对其请求进行标注的实体(通常是相关领域专业人员),即主动学习是交互进行的。而半监督学习指的是学习算法不需要人工干预,基于自身对未标记数据加以利用。
9、提高类不平衡数据的分类准确率一般方法包括(1)过采样(2)欠采样(3)阈值移动(4)组合技术
过采样与欠采样改变训练集的分布;阈值移动影响对新数据分类时模型如何决策。
10、关于K均值聚类,算法快速,简单;聚类中心点可变;时间复杂度接近于线性。
11、线性分类器三种最优准则:
- Fisher准则:根据两类样本一般类内密集, 类间分离的特点,寻找线性分类器最佳的法线向量方向,使两类样本在该方向上的投影满足类内尽可能密集,类间尽可能分开。该种度量通过类内离散矩阵Sw和类间离散矩阵Sb实现。
- 感知准则:准则函数以使错分类样本到分界面距离之和最小为原则。其优点是通过错分类样本提供的信息对分类器函数进行修正,这种准则是人工神经元网络多层感知器的基础。
- 支持向量机:基本思想是在两类线性可分条件下,所设计的分类器界面使两类之间的间隔为最大, 它的基本出发点是使期望泛化风险尽可能小
12、函数
- strcat:连接两个字符串
- strcpy:将一个字符串的一部分拷贝到另一个字符串中
- strcmp:比较两个字符串的大小关系
- Strlen:获得字符串长度
13、自顶向下的语法分析方法:
(1)递归子程序法(2)LL(1)分析法
自底向上的分析技术 有:
( 1 )简单优先分析法
( 2 )算符优先分析法
( 3 )优先函数
( 4 ) LR 分析法
14、CPI( Cycles Per Instruction)表示每条计算机指令执行所需的时钟周期,有时简称为指令的平均周期数。
15、类域界面方程法中,不能求线性不可分情况下分类问题近似或精确解的方法是( 感知器算法 )
16、并发操作指的是多用户或多事务同时对同一数据进行操作。
当两个或多个事务选择同一数据,并且基于最初选定的值修改该数据时,会发生丢失修改问题。每个事务都不知道其它事务的存在,最后的更新将重写由其它事务所做的更新,这将导致修改丢失。
当一个事务正在访问数据,并且对数据进行了修改,而这种修改还没有提交到数据库中,这时,另外一个事务也访问这个数据,然后使用了这个数据。因为这个数据是还没有提交的数据,那么另外一个事务读到的这个数据是脏数据。
一个事务重新读取前面读取过的数据,发现该数据已经被另一个已提交的事务修改过。即事务1读取某一数据后,事务2对其做了修改,当事务1再次读数据时,得到的与第一次不同的值。在一个事务中前后两次读取的结果并不致,导致了不可重复读。
17、连通图是指任意两个结点之间都有一个路径相连,对于n个顶点的连通图,至少需要n-1条边。
完全图是指任意两个结点之间都有一个边相连,也就是结点两两相连,至少需要n*(n-1)/2条边。
18、散列表(哈希表)中处理冲突的方法有:开放定址(Open Addressing)法,一旦发生了冲突,就去寻找下一个空的散列地址。
按照探查方法不同:线性探查法、 二次探查法、 双重散列法等
拉链(Chaining)法是将所有关键字为同义词的结点链接在同一个单链表中。
拉链法处理冲突简单,且无堆积现象,即非同义词决不会发生冲突,因此平均查找长度较短。
2018.9.17
1、KMP算法是一种改进的字符串匹配算法,由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现,因此人们称它为克努特——莫里斯——普拉特操作(简称KMP算法)。KMP算法的关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数,函数本身包含了模式串的局部匹配信息。时间复杂度O(m+n)。
在KMP算法中,对于每一个模式串我们会事先计算出模式串的内部匹配信息,在匹配失败时最大的移动模式串,以减少匹配次数。
kmp算法中,文本中的指针i是无法回溯的,所以最关键的是,next[j]的值(也就是k)表示,当P[j] != T[i]时,j指针的下一步移动位置。其中P为匹配字符串,T为原文。也就是说next数组其实就是查找P中每一位前面的子串的前后缀有多少位匹配,从而决定j失配时应该回退到哪个位置。
而在计算next数组时主要是以下两个步骤:
- 1. 当P[k] == P[j]时,有next[j+1] == next[j] + 1。
- 2. 当P[k] != P[j]时,有k = next[k]。
结合1和2可知,next[j]==k;也就是说,P[0 ~ k-1] == p[j-k ~ j-1]中k的位置决定了next[j]的值。
https://www.cnblogs.com/tangzhengyue/p/4315393.html
2、旅行商问题(TravelingSalesmanProblem,TSP)是一个经典的组合优化问题。经典的TSP可以描述为:一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总的行程最短。从图论 的角度来看,该问题实质是在一个带权完全无向图中,找一个权值最小的Hamilton 回路。由于该问题的可行解是所有顶点的全排列 ,随着顶点数的增加,会产生组合爆炸,它是一个NP完全问题 。由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用,国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题,常用的方法包括:分枝定界法、线性规划法、动态规划法等。但是,随着问题规模的增大,精确算法将变得无能为力,因此,在后来的研究中,国内外学者重点使用近似算法或启发式算法 ,主要有遗传算法 、模拟退火法 、蚁群算法 、禁忌搜索 算法、贪婪算法和神经网络等。
3、NP问题是指存在多项式算法能够解决的非决定性问题,而其中NP完全问题又是最有可能不是P问题的问题类型。NP问题是指可以在多项式的时间里验证一个解的问题。
那些可以在多项式( polynomial )时间内解决的问题,称为P问题。所有的P类问题都是NP问题。
NP-hard是其解的正确性能够被“很容易检查”的问题,这里“很容易检查”指的是存在一个多项式检查算法。相应的,若NP中所有问题到某一个问题是图灵可归约的,则该问题为NP困难问题。
通常所谓的“NP问题”,其实就一句话:证明或推翻P=NP。因为这个问题还未解决,所以有以下两种关系:
