盲源分离(Blind Source Separation, BSS)是解决“鸡尾酒会问题(The Cocktail Party Problem)”的利器之一,其目的就是要将各个源信号,或后续问题中需要用到的某个或某些源信号从观测得到的混合信号中分离出来。所谓“盲源”,指的是源信号本身的波形、源信号的数目、信号源的位置等关于源信号的先验知识,以及观测点的位置、混合环境的信息等关于混合环境的先验知识未知,需要仅从观测信号中进行分离。
从混合方式来看,盲源分离研究的信号模型主要有三种:线性混合模型、卷积混合模型和非线性混合模型。
独立成分分析
在实际应用中,只有观测信号x是已知的,源信号和信道信息都未知。为了能从有限的条件中求解问题,必须对当前问题做进一步的假设和限定。
最常用的一种假设即独立性假设:由于不同的源信号是不同的物理过程产生的,所以可以假设各个源之间是相互独立的。将各个源信号看成是相互独立的随机过程所产生的随机变量,根据概率论中的“中心极限定理”:多个相互独立的随机变量相互叠加,其结果越趋近于高斯分布。所以观测信号比源信号就更趋近于高斯分布,而分离的过程就是不断调整分离向量,使得输出信号的非高斯性,以及各个输出分量的独立性达到最大的过程。
这类与独立性为前提的方法也叫做独立成分分析(Independent Component Analysis, ICA),是最典型的盲源分离方法之一。
使用盲源分离技术进行噪声抑制,最大的好处就在于其“盲源”的特性,即不需要对声源位置及麦克风阵列拓扑结构做过多的要求就可以实现对声源的分离,所以极大的拓宽了该技术的应用场景。
ICA的具体原理和计算方式见:独立成分分析(Independent component analysis, ICA)
峭度
盲源分离常用的方法是ICA(independent component analysis),而ICA算法又是基于非高斯分布假设的,目标是使得非高斯性最大化。因此了解问题所涉及的变量是不是高斯分布,决定了是否能用ICA算法。
Kurtosis是反映随机变量分布特性的数值统计量,是归一化4阶中心矩。峭度是衡量随机信号特征的四阶量。三阶为斜度。一般的非高斯信号都以峭度斜度来衡量。又称为峰度。
在统计学中,峰度(Kurtosis)衡量实数随机变量概率分布的峰态。峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。
根据均值不等式,可以确定出峰度(系数)的取值范围:它的下限不会低于1,上限不会高于数据的个数。
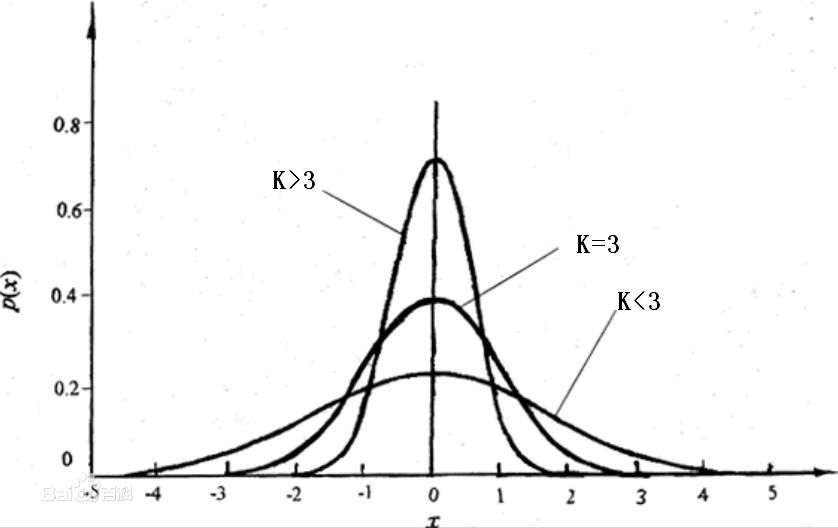
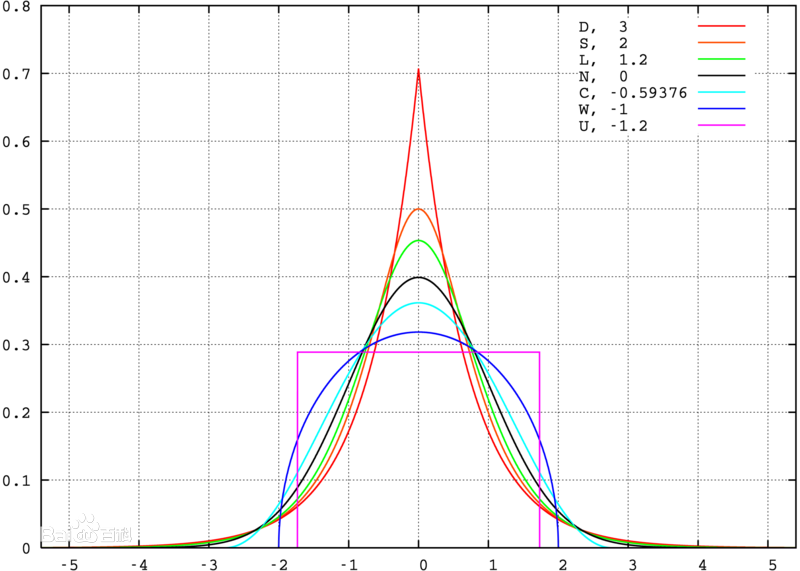
正态分布的峰度(系数)为常数3,均匀分布的峰度(系数)为常数1.8。在统计实践中,我们经常把这两个典型的分布曲线作为评价样本数据序列分布性态的参照。设若先将数据标准化,则峰度(系数)相当于标准化数据序列的四阶中心矩。所以,在相同的标准差下,峰度系数越大,分布就有更多的极端值,那么其余值必然要更加集中在众数周围,其分布必然就更加陡峭。在实际应用中,通常将峰度值做减3处理,使得正态分布的峰度0。
峰度定义为四阶标准矩:
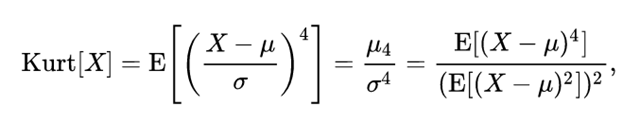
样本峰度计算公式: