期望最大化算法EM。
简介
EM算法即期望最大化算法,由Dempster等人在1976年提出[1]。这是一种迭代法,用于求解含有隐变量的最大似然估计、最大后验概率估计问题。至于什么是隐变量,在后面会详细解释。EM算法在机器学习中有大量成功的应用,典型是求解高斯混合模型,隐马尔可夫模型。如果你要求解的机器学习模型中有隐变量存在,并且要估计模型的参数,EM算法很多时候是首选算法。
EM算法的推导、收敛性证明依赖于Jensen不等式,我们先对它做一简单介绍。Jensen不等式的表述是,如果f(x)是凸函数,x是随机变量,则下面不等式成立
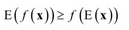
在这里E是数学期望,对于离散型随机变量,数学期望是求和,对连续型随机变量则为求定积分。如果f(x)是一个严格凸函数,当且仅当x是常数时不等式取等号:

EM算法的目标是求解似然函数或后验概率的极值,而样本中具有无法观测的隐含变量。
应用原理
有人称之为上帝算法,只要有一些训练数据,再定义一个最大化函数,采用EM算法,利用计算机经过若干次迭代,就可以得到所需的模型。EM算法是自收敛的分类算法,既不需要事先设定类别也不需要数据见的两两比较合并等操作。缺点是当所要优化的函数不是凸函数时,EM算法容易给出局部最佳解,而不是最优解。
在统计计算中,最大期望(EM)算法是在概率(probabilistic)模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐藏变量(Latent Variable)。
EM经常用在机器学习和计算机视觉的数据聚类(Data Clustering)领域。
EM算法用于寻找隐藏参数的最大似然估计。该算法首先在E step中计算隐藏参数的似然估计,然后再M step中进行最大化,然后进行EM step的迭代直至收敛。应用场景之一是聚类问题,但EM算法本身并不是一个聚类算法。举个例子,GMM(高斯混合模型)和Kmeans在聚类时都使用了EM算法。
EM 算法还是许多非监督聚类算法的基础(如 Cheeseman et al. 1988 ),而且它是用于学习部分可观察马尔可夫模型( Partially Observable Markov Model )的广泛使用的 Baum-Welch 前向后向算法的基础。
总结来说,EM算法就是通过迭代,最大化完整数据的对数似然函数的期望,来最大化不完整数据的对数似然函数。
参考文献
[1] Arthur P Dempster, Nan M Laird, Donald B Rubin. Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the royal statistical society series b-methodological, 1976.