堆和堆排序

一、什么是优先队列？

普通队列：先进先出，后进后出

优先队列：出队顺序和入队顺序无关，和优先级相关。

优先队列的实现：

	入队	出队
普通数组	O(1)	O(n)
顺序数组	O(N)	O(1)
堆	O(logN)	O(logN)

二、堆的基本实现

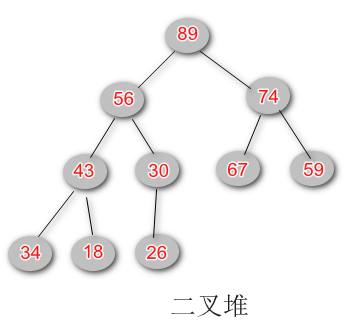
二叉堆的特点：这很重要！！！ 是核心

• 任意节点小于其父节点
• 除了最后一层叶子节点外，其他层的元素个数必须是最大值 ，叶子节点虽然可以不是最大值，但必须靠左排列(最大堆)
• 堆是一棵完全二叉树

用数组存储二叉堆

　　

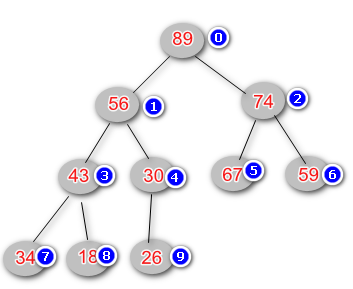
这样用数组存储的堆中元素和数组下标有以下规律：  这很重要！！！ 是核心

• • 父节点下标：parent (i) = ( i - 1) / 2
  • 左子节点： left child (i)  = (i + 1) * 2 
  • 右子节点：right child (i) = (i + 1) * 2 + 1 

最大堆代码实现 (逐步的实现，下面只是简单的定义，各种操作的方法后续依次加入) ：

public class MaxHeap {

    // 存储元素
    private int[] data;
    // 记录堆中节点个数
    private int size;
    // 堆的容量
    private int capacity;

    public MaxHeap(int capacity) {

        this.capacity = capacity;
        data = new int[capacity]; // 堆的第一个元素索引为 0;
        this.size = 0;
    }

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }

}

往最大堆中添加元素(shiftUp)

　                                  　

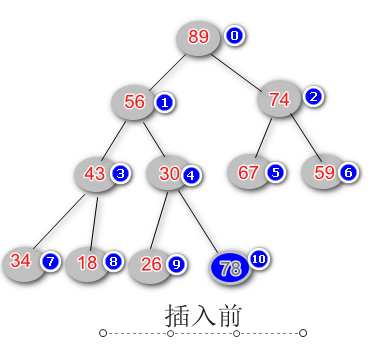
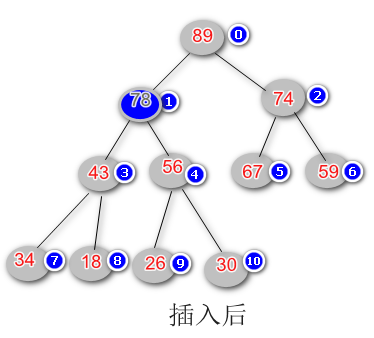
根据前面对最大堆的定义(任意子节点小于其父节点) 以及元素下标之间的关系，我们不断交换父子节点的位置，知道满足最大堆的原则，就完成了元素插入。下面是代码实现：

    /**
     * 往最大堆中加入一个元素
     * @param e 
     */
    public void insert(int e) {

        if (size - 1 < capacity) {
            data[size] = e;
            shiftUp(size);
            size++;
        }
    }

    /**
     * 根据堆的定义，交换父子节点的位置，直到满足最大堆的原则
     * @param k
     */
    private void shiftUp(int k) {

        while (k > 0 && data[k] > data[(k - 1) / 2]) {
            SortedHandler.swap(data, k, (k - 1) / 2);
            k = (k - 1) / 2;
        }
    }

删除最大堆中的元素(shiftDown)

            

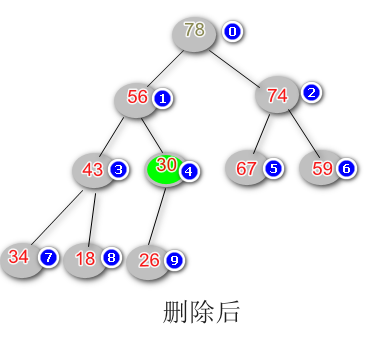
　　根据优先队列的定义，元素的出顺序按照优先级，而在最大堆中，根节点的优先级就是最大的，因此我们删除的时候，总是从根节点开始。

　　具体的思路是，首先交换根节点和最后一个节点的位置，然后删除掉交换后的根节点，也就是最大值，然后根据堆的定义交换节点位置维护最大堆的原则，最后返回删除了的最大值即可。代码实现如下：

    /**
     * 交换根节点和最后一个节点的位置，再将移除的根节点的值返回，并维护最大堆的原则
     * @return 原堆中的最大值
     */
    public int extractMax() {

        if (size > 0) {
            int res = data[0];

            // 交换第一个和最后一个的位置
            SortedHandler.swap(data, 0, size - 1);
            size--;
            shiftDown(0);
            return res;
        }

        return -1;
    }

    /**
     * 交换节点的位置  维护最大堆的定义
     * @param k 开始的节点位置
     */
    private void shiftDown(int k) {

        while (2 * k + 1 < size) {
            int j = 2 * k + 1; // 左子点的下标
            if (j + 1 < size && data[j + 1] > data[j]) {
                j += 1;
            }
            if (data[k] < data[j]) {
                SortedHandler.swap(data, k, j);
                k = j;
            } else {
                break;
            }
        }

    }

 三、基本的堆排序

　　通过上面的努力，我们实现了一个基本操作的最大堆。如果前面的明白了的话，那么实现一个堆排序就是小问题了，因为我们的最大堆的输出顺序就是由大到小的，那么排序的问题不过是将数组的顺序反过来 .

    public static void heapSorted1(int arr[]) {

        int n = arr.length;
        MaxHeap heap = new MaxHeap(n);

        for (int i = 0; i < n; i++) {
            heap.insert(arr[i]);
        }
        for (int i = n - 1; i >= 0; i--) {
            arr[i] = heap.extractMax();
        }
    }

 最大堆的另外一种构造方法 —— Heapify

　　在前面构造最大堆的实现中，我们都是首先构造一个初始化容量的数组，然后依次加入数组的每个元素。现在我们考虑一个情况，因为最大堆的存储本身就是数组实现的，那么当我们对数组需要排序的时候，是否可以直接将这个数组构造成为最大堆呢，而无需逐个的复制元素并shiftUp？答案是肯定的。

　　具体的思路是：将待排序的数组本身看成是一棵二叉树，在这课二叉树中，所有不同的非叶子节点就是不用的最大堆。那么我们就从这棵二叉树的第一个非叶子节点开始执行shiftDown操作，直到整棵二叉树满足最大堆的原则。那么问题又来了？第一个非叶子是多少呢，这里又有一个规律：完全二叉树的排列中，第一个非叶子节点 i 等于数组的长度 (n - 1) / 2.代码实现如下：

    // heapify 的过程
    public MaxHeap(int arr[]) {

        int n = arr.length;
        data = new int[n];
        capacity = n;
        for (int i = 0; i < n; i++) {
            data[i] = arr[i];
        }
        size = n;
        // 第一个非叶子节点的下标 (n-1) / 2
        for (int i = (n - 1) / 2; i >= 0; i--) {
            shiftDown(i);
        }

    }

    public static void heapSorted2(int arr[]) {

        int n = arr.length;
        MaxHeap heap = new MaxHeap(arr);

        for (int i = n - 1; i >= 0; i--) {
            arr[i] = heap.extractMax();
        }

    }

四、堆排序的优化——原地堆排序

    public static void heapSorted3(int arr[]) {

        int n = arr.length;
        
        // heapify ,将数组转换为堆
        for (int i = (n - 1) / 2; i >= 0; i--) {
            __shiftDown(arr, n, i);
        }

        // 
        for (int i = n - 1; i > 0; i--) {
            int tmp = arr[i];
            arr[i] = arr[0];
            arr[0] = tmp;

            __shiftDown(arr, i, 0);
        }

    }

    /**
     *  原地堆排序的shiftDown操作
     * @param arr
     * @param n
     * @param i
     */
    private static void __shiftDown(int[] arr, int n, int i) {

        while (2 * i + 1 < n) {
            int j = 2 * i + 1;
            if (j + 1 < n && arr[j] < arr[j + 1]) {
                j += 1;
            }
            if (arr[j] > arr[i]) {
                int tmp = arr[j];
                arr[j] = arr[i];
                arr[i] = tmp;

                i = j;
            } else
                break;
        }

    }