Spark MLlib机器学习概论

一.什么是机器学习？

　　什么是机器学习？Herbert Sinmon给“学习”做出了这样的定义：“如果一个系统能够通过执行某个过程而改进性能，这就是学习。”更通俗的理解是：机器学习能够自动地从数据中学习“程序”，而这个程序不是人来编写的。

　　平面上有两类点，黄色代表类别a，蓝色代表类别b。这时我们希望能够找到平面上的一条曲线，将两个类别的点分成两个平面，使类别a属于平面A，类别b属于平面B。这样一来，对于一个新出现的颜色未知的点x，我们通过查看点落在平面A还是平面B中来判断x属于哪个类别。

　　

　　当然，这个任务从人的视觉来看似比较容易完成的。人也可以将这个曲线用一个数学表达式来表示，但这个曲线方程是确定的，当观察到的数据发生变化时，需要重新调整方式，因此扩展性并不好。机器能够根据已经观测到的两个类别不同的情况自动给出不同的曲线表达式，这里的曲线就是我们常说的学习到的模型。这是一个有监督学习的典型案例。

　　这个案例中自动寻找曲线的算法是由SVM程序完成的。如今，机器学习已经被广泛应用于各个领域，例如：

• 图像识别。人脸识别，可以识别图像中人脸的位置。
• 语音识别。将声音转换为文字，例如小米的小爱。
• 文本识别。拼写纠错，搜索引擎大量应用文本挖掘

二.机器学习案例

　　要估计腾讯大厦的具体高度，需要根据多次测量来估算大厦的精确高度。

　　

　　测量的具体过程是将卷尺从顶楼抛到地面来读数测量。由于大楼表面凹凸不平，以及风力等原因，每次读到的数据都不太一样。那么，大厦精确的高度应该是多少呢？假设实际高度是193.2米，我们称实际高度为理论值。我们可能永远不知道理论值具体是多少，但可以让估计值尽可能接近这个理论值。

　　最小二乘法就是一个这样的理论。它定义多次测量值的误差之和为累计误差：

　　累计误差=∑(观测值-理论值)²

　　我们用g(x)表示其累计误差，x表示理论值的估计值，x_i表示第i次测量，得到数学表达式：

　　

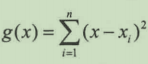
　　这里x_{i为已知值，依据最小二乘法可知，当累积误差最小时，我们就得到一个最接近理论值的估计值。这是求函数极值的常见方法。我们对x求导，得到公式：}

　　

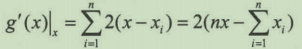
　　导数为0时，g(x)取极小值，求解方程得：

　　

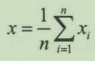
　　估计值等于各次观测值的平均值。

　　所以，我们日常中使用多次测量求平均值的做法是有严格数学依据的。当然，这个案例比较简单，在机器学习的其它问题中，问题的抽象和求解可能要比这复杂的多。

三.机器学习的基本方法

　　机器学习已经形成了一套完善的方法论，在很多文献中指出“机器学习=模型+策略+算法”。如下：

• 模型model。计算机如何表达要解决的问题，就是机器学习的模型，这里使用函数来表达，具体函数实现就是求均值。
• 策略strategy。模型通常是有参数的。所有可能 的模型有很多，如何评估模型的优劣就是机器学习的策略。这里通过计算误差平方和评估模型的优劣，这个误差平方通常叫做平方损失函数。
• 算法algorithm。损失函数评估模型的优劣通常通过一个搜索算法来找到最优的模型，这里通过函数求导来搜索损失函数值最小的算法，借此来选择最优模型。

　　机器学习的方法丰富多样，模型可以是函数，常见的还有概率分布；策略可以是平方和最小，常见的损失函数还有0-1损失函数、绝对损失函数、对数损失函数等；算法可以是求导，也可以是EM算法等。

　　机器学习的一般过程大致可以分为以下几个步骤：

1. 准备训练数据集合。
2. 选择算法模型。
3. 选择学习策略。
4. 实现求解最优模型的算法。
5. 使用新数据对模型进行评估，找出最优模型。
6. 使用最优模型对新数据进行预测。

　　基本过程如下：

　　

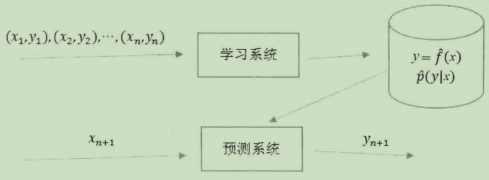
四.机器学习的常用技巧

　　首先，在准备训练数据时，训练数据要注意满足以下两点：

1. 尽可能和应用场景实际数据类似。
2. 训练数据尽可能充分，而且充足。

　　为了防止过拟合和模型验证，通常会把训练数据分为训练集、验证集和测试集。训练集用于训练模型，验证集用于模型选择，测试集用于模型评估。

　　选择好训练样本后，需要将其通过特征向量表示成算法能够理解的形式。特征的数值类型表示形式如下：

• 浮点数特征。比如商品价格。
• 离散值特征。比如商品颜色，用每个数字表示一种颜色。
• 二值特征。比如一个广告标签中是否有“打折”这个词作为特征，有则特征值为1，否则则为0。

　　其中，直接使用浮点数特征时，如果不同特征取值范围差异较大，可能导致学习的模型不是最优解。需要把不同特征的取值都映射到相同的范围内，通常通过归一化方法进行缩放，还需要处理缺失值和异常值，异常值比如分数范围0~100，存在不在范围的分数。当特征空间比较大时，需要做特征提取。这时，应该选择信息增益大的特征，否则模型会太大，训练和预测效率都会比较低。在特征选择上，一方面不是特征越多越好，特征之间可能携带的信息有重合；另一方面则需要保证特征包含足够区分需要识别的对象的信息。业界的一些系统已经能够做到部分机器学习算法自动选择特征的过程。

　　选择模型上，不是越复杂的模型越好，也没有万能的模型，往往诠释要解决的问题本身比理解模型更难。模型选择一般还要考虑以下几点：

• 训练时间。随着观测数据的变化，需要重新训练模型，训练新模型的时间不能太长。
• 预测时间。模型上线工作的时候，对新输入的数据进行预测得分所需要的时间。
• 模型存储。模型运行的时候需要多少内存空间。

　　一般模型需要多次调优才能取得较好的效果，这个时候分析案例往往能够洞察你的问题。比如，如果发现预测效果不好的样本普遍存在某个规律，通常我们会从细分的各个维度去分析模型的效果，来确定下一步的优化方向。

　　实际工程应用中，准备数据和特征提取往往占据比较大的比例。