题目描述:
给定一个没有重复数字的序列,返回其所有可能的全排列。 示例: 输入: [1,2,3] 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
题目解析:来自leetcode@liweiwei1419
以示例输入: [1, 2, 3] 为例,如果让我们手写,要做到不重不漏,我们书写的策略可能是这样:“一位一位确定”,这样说比较笼统,具体是这样的:
1、先写以 1 开始的两个排列:[1, 2, 3]、[1, 3, 2];
2、再写以 2 开始的两个排列:[2, 1, 3]、[2, 3, 1];
3、最后写以 3 开始的两个排列:[3, 1, 2]、[3, 2, 1]。
如果数组元素多一点的话,也不怕,我们写的时候遵循下面的原则即可:
1、按数组的顺序来(不要求排序,但我们选取元素的顺序是从左到右的),每次排定 1 个元素;
说明:只有按照顺序才能做到不重不漏。
2、新排定的元素一定不能在之前排定的元素中出现。
说明:如果违反了这一条,就不符合“全排列”的定义。
其实让程序帮你找到所有的全排列也是这样的思路。如果不是这样的话,我们要写数组长度这么多层的循环,编码极其困难,代码写出来也非常不好看。
这道题可以作为理解“回溯算法”的入门题。这是一个非常典型的使用 回溯算法 解决的问题。解决回溯问题,我的经验是 一定不要偷懒,拿起纸和笔,把这个问题的递归结构画出来,一般而言,是一个树形结构,这样思路和代码就会比较清晰了。而写代码即是将画出的图用代码表现出来。
思路分析:
方法:“回溯搜索”算法即“深度优先遍历 + 状态重置 + 剪枝”(这道题没有剪枝)
以示例输入: [1, 2, 3] 为例,因为是排列问题,只要我们按照顺序选取数字,保证上一层选过的数字不在下一层出现,就能够得到不重不漏的所有排列。
说明:这里“保证上一层选过的数字不在下一层出现”的意思是我们手写的时候,后面选的数字一定不能是前面已经出现过的。为了做到这一点,我们得使用一个数组长度这么长的额外空间,记为数组 used ,只要“上一层”选了一个元素,我们就得“标记一下”,“表示占位”。
画出树形结构如下图,
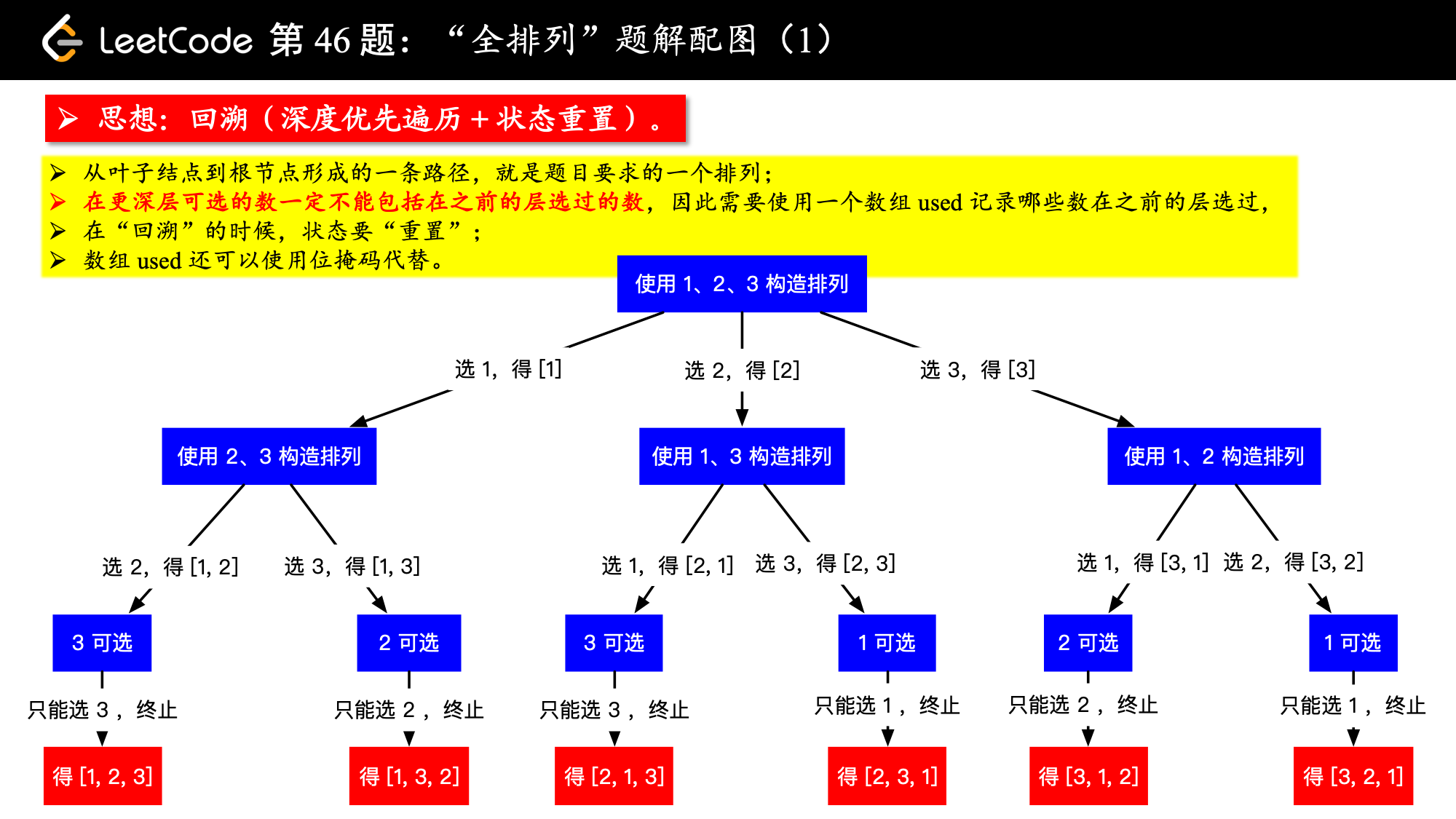
这里我们介绍什么是“状态”。
在递归树里,辅助数组 used 记录的情况和当前已经选出数组成的一个排序,我们统称为当前的“状态”。
注意:
1、这里特别说明一点:虽然我的图是一下子展示出来的,但是我想你画出的图应该是一层一层画出来的;
2、在每一层,我们都有若干条分支供我们选择。下一层的分支数比上一层少 1 ,因为每一层都会排定 1 个数,从这个角度,再来理解一下为什么要使用额外空间记录那些元素使用过;
3、全部的“排列”正是在这棵递归树的所有叶子结点。
我们把上面这件事情给一个形式化的描述:问题的解空间是一棵递归树,求解的过程正是在这棵递归树上搜索答案,而搜索的路径是“深度优先遍历”,它的特点是“不撞南墙不回头”。
下面解释“状态重置”。
在程序执行到上面这棵树的叶子结点的时候,此时递归到底,当前根结点到叶子结点走过的路径就构成一个全排列,把它加入结果集,我把这一步称之为“结算”。此时递归方法要返回了,对于方法返回以后,要做两件事情:
(1)释放对最后一个数的占用;
(2)将最后一个数从当前选取的排列中弹出。
事实上在每一层的方法执行完毕,即将要返回的时候都需要这么做。这棵树上的每一个结点都会被访问 2 次,绕一圈回到第 1 次来到的那个结点,第 2 次回到结点的“状态”要和第 1 次来到这个结点时候的“状态”相同,这种程序员赋予程序的操作叫做“状态重置”。
“状态重置”是“回溯”的重要操作,“回溯搜索”是有方向的搜索,否则我们要写多重循环,代码量不可控。
说明:
1、数组 used 记录了索引 i 在递归过程中是否被使用过,还可以用哈希表、位图来代替,在下面的参考代码 2 和参考代码 3 分别提供了 Java 的代码;
2、当程序第 1 次走到一个结点的时候,表示考虑一个数,要把它加入列表,经过更深层的递归又回到这个结点的时候,需要“状态重置”、“恢复现场”,需要把之前考虑的那个数从末尾弹出,这都是在一个列表的末尾操作,最合适的数据结构是栈(Stack)。
请大家在脑子里想一想程序在这棵递归树上“深度优先遍历”执行的路径,理解了“状态重置”这个概念,是不是觉得“回溯搜索”这个名字很形象。
如果序列包含重复数字,这就是 「力扣」第 47 题:“全排列 II”,需要做“剪枝”操作,做法可以参考《回溯 + 剪枝(Python 代码、Java 代码)》。
参考代码 1 是全排列问题我个人觉得比较好的写法,可以作为写回溯算法的模板,类似的问题写出来的代码基本都是这个样子。
代码实现:
package com.company;
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
/**
* @author yaoshw
*/
public class Main {
public static void main(String[] args) {
int[] nums = new int[]{1, 2, 3};
List<List<Integer>> result = permute(nums);
result.forEach(System.out::println);
}
public static List<List<Integer>> permute(int[] nums) {
int len = nums.length;
List<List<Integer>> result = new ArrayList<>();
if (len == 0) {
return result;
}
boolean[] used = new boolean[len];
generatePermute(nums, used, 0, len, new Stack<>(), result);
return result;
}
/**
* @param nums 输入的数组
* @param visited 标记某一位是否在当前搜索中被访问的状态
* @param curSize 当前索引,即搜索在哪一层了
* @param len 数组的长度
* @param path 一次搜索的结果集,即一条路径上的值的组合
* @param result 全排列
* @return 数组内元素的全排列
*/
private static void generatePermute(int[] nums, boolean[] visited, int curSize, int len, Stack<Integer> path, List<List<Integer>> result) {
if (curSize == len) {
result.add(new ArrayList<>(path));
}
for (int i = 0; i < len; i++) {
//当前值没有被访问时,将其加入到当前序列中
if (!visited[i]) {
path.push(nums[i]);
visited[i] = true;
generatePermute(nums, visited, curSize + 1, len, path, result);
//回溯前后,状态重置
path.pop();
visited[i] = false;
}
}
}
}
时间复杂度:O(∑ k=1N P(N,k)), P(N, k) = {N!}{(N - k)!} = N (N - 1) ... (N - k + 1),该式被称作 n 的 k-排列,或者_部分排列。
空间复杂度:O(N!) 由于必须要保存N!个解。