题目描述:
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
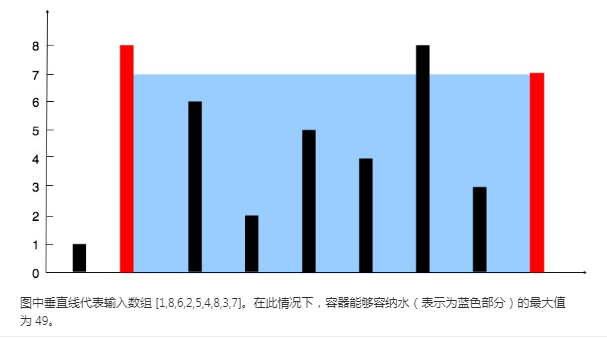
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49
题目解析:
定义 i 和 j 两个指针分别指向数组的左右两端,然后两个指针向中间搜索,并且更新面积最大值 res,直到 i == j 时返回 res。
其中 容器装水量的算法是找出左右两个边缘中较小的那个乘以两边缘的距离。
代码实现:
package com.company;
public class Main {
public static void main(String[] args) {
// write your code here
int[] arr = new int[]{1, 8, 6, 2, 5, 4, 8, 3, 7};
System.out.println(maxArea(arr));
}
private static int maxArea(int[] height) {
int result = 0;
int left = 0;
int right = height.length - 1;
while (left < right) {
result = (height[left] < height[right]) ? Math.max(result, (right - left) * height[left++])
: Math.max(result, (right - left) * height[right--]);
}
return result;
}
}
时间复杂度:O(N),双指针遍历一次底边宽度 N 。
空间复杂度:O(1),指针使用常数额外空间。