poj 1419Graph Coloring 【dfs+补图+计算最大团+计算最大独立集 【模板】】

题目地址：http://poj.org/problem?id=1419

Graph Coloring

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 4468		Accepted: 2042		Special Judge

Description

You are to write a program that tries to find an optimal coloring for a given graph. Colors are applied to the nodes of the graph and the only available colors are black and white. The coloring of the graph is called optimal if a maximum of nodes is black. The coloring is restricted by the rule that no two connected nodes may be black.



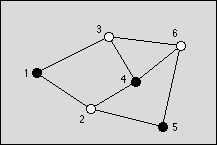
Figure 1: An optimal graph with three black nodes

Input

The graph is given as a set of nodes denoted by numbers 1...n, n <= 100, and a set of undirected edges denoted by pairs of node numbers (n1, n2), n1 != n2. The input file contains m graphs. The number m is given on the first line. The first line of each graph contains n and k, the number of nodes and the number of edges, respectively. The following k lines contain the edges given by a pair of node numbers, which are separated by a space.

Output

The output should consists of 2m lines, two lines for each graph found in the input file. The first line of should contain the maximum number of nodes that can be colored black in the graph. The second line should contain one possible optimal coloring. It is given by the list of black nodes, separated by a blank.

Sample Input

1
6 8
1 2
1 3
2 4
2 5
3 4
3 6
4 6
5 6

Sample Output

3
1 4 5
题目解读：对于一个给定的图找出一个最佳的着色。对图中的节点进行着色，只能用黑色或白色，着色的规则就是两个相邻的节点不能都是黑色。
（当然有可能是白色）T组数据，每组有n个节点，m条边。也就是要求当前图的最大独立集。
算法实现：通过求补图上的最大团来计算当前图的最大独立集。补图直接在输入边的时候就构建，采用规定模式计算补图最大团。

代码：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <ctype.h>
#include <math.h>
#include <iostream>
#include <string>
#include <queue>
#include <algorithm>
#define N 105

using namespace std;

int n, m;
bool g[N][N];
int get[N][N];
int node[N], ans[N], dp[N];

int Max; //当前团的节点数为Max


void dfs(int now, int sum)
{         //从当前状态（当前团的节点数为now 与其中最后节点相连的边数为sum）出发，递归计算最大团
    if(sum==0){  //若构成团 即完全子图
        if(now > Max){
            Max=now;
            for(int i=1; i<=Max; i++)
                ans[i]=node[i];  //存储团中的节点
        }
        return ;
    }
    for(int i=1; i<=sum; i++){
        int v=get[now][i], t=0;
        if(now+dp[v]<=Max) return ;
        for(int j=i+1; j<=sum; j++){
            if(g[v][get[now][j]] )
                get[now+1][++t]=get[now][j];
        }
        node[now+1]=v;
        dfs(now+1, t);
    }
}

void init()
{
    scanf("%d %d", &n, &m);
    memset(g, true, sizeof(g)); //补图初始化 边之间互相连通
    for(int i=0; i<m; i++){
        int u, v;
        scanf("%d %d", &u, &v);
        g[u][v]=false; g[v][u]=false; //补图中应该断开
    }
}

void solve() //计算和输出补图的最大团 即是原图的最大独立集
{
    Max=0; //
    for(int i=n; i>=1; i--){ //按照递减顺序将每个节点i作为当前团的首节点
        int sum=0;
        for(int j=i+1; j<=n; j++){ //计算i+1...n中与i相邻的端点，将其存入get[1][]
            if(g[i][j]) get[1][++sum]=j;
        }
        node[1]=i;
        dfs(1, sum);
        dp[i]=Max;
    }
    printf("%d
", Max);
    for(int i=1; i<=Max-1; i++){
        printf("%d ", ans[i]);
    }
    printf("%d
", ans[Max]);
}

int main(void)
{
    int tg;
    scanf("%d", &tg);
    while(tg--){
        init();
        solve();
    }
    return 0;
}