题目描述
要爬N阶楼梯,每次你可以走一阶或者两阶,问到N阶有多少种走法
测试样例
Input: 2
Output: 2
Explanation: 到第二阶有2种走法
1. 1 步 + 1 步
2. 2 步
Input: 3
Output: 3
Explanation: 到第三阶有3种走法
1. 1 步 + 1 步 + 1 步
2. 1 步 + 2 步
3. 2 步 + 1 步
详细分析
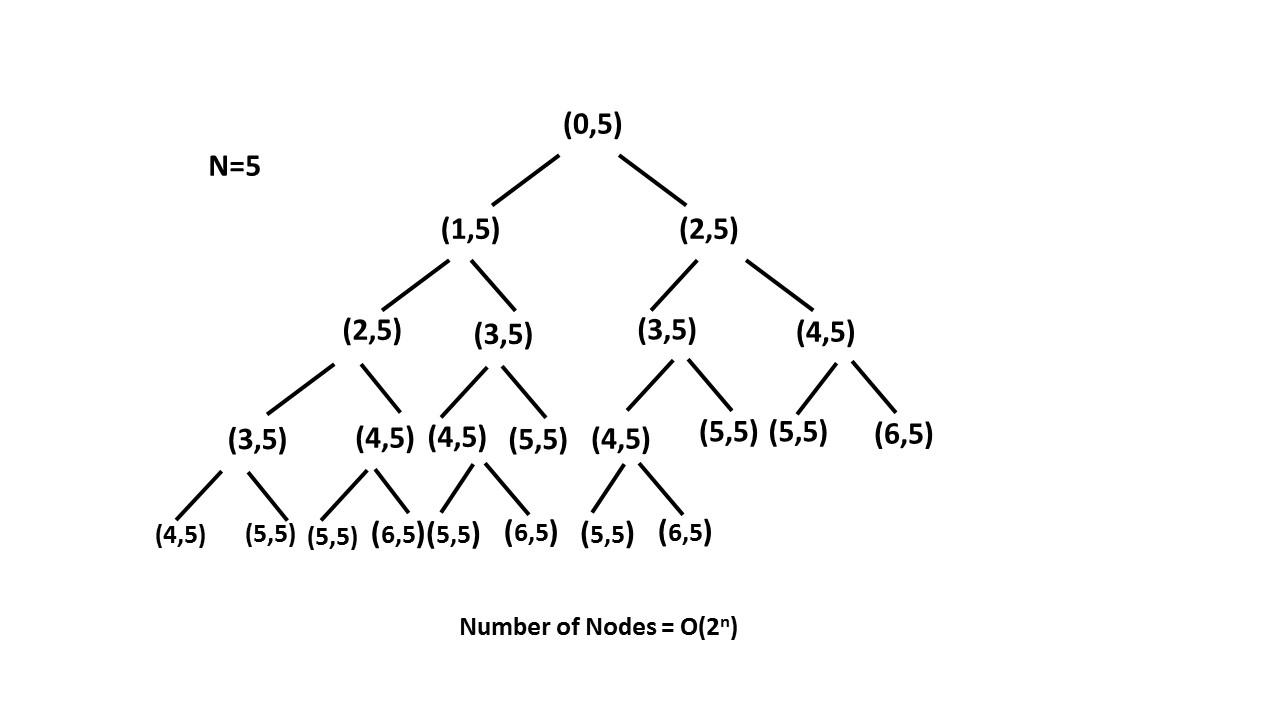
在第0阶,可以选择走到第1阶或者第2阶,第1阶可以走第2阶或者第3阶,第二阶可以走第3阶或者第4阶...。如此继续就生成了上图递归解答树。注意如果直接递归会超时,当前实现使用了记忆化储存子解。
算法实现
记忆化递归(√)
class Solution { public: int climbStairs(int n) { this->n = n; memo = new int[n+2]; for(int i=0;i<n+2;i++){ memo[i] = -1; } return recursiveClimbing(0); } int recursiveClimbing(int currentStep){ if(memo[currentStep]!=-1){ return memo[currentStep]; } if(currentStep==n){ return 1; } if(currentStep>n){ return 0; } memo[currentStep] = recursiveClimbing(currentStep+1) + recursiveClimbing(currentStep+2); return memo[currentStep]; } private: int n; int total = 0; int *memo; };