题目描述
某国有n个城市,它们互相之间没有公路相通,因此交通十分不便。为解决这一“行路难”的问题,政府决定修建公路。修建公路的任务由各城市共同完成。
修建工程分若干轮完成。在每一轮中,每个城市选择一个与它最近的城市,申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。
政府审批的规则如下:
(1)如果两个或以上城市申请修建同一条公路,则让它们共同修建;
(2)如果三个或以上的城市申请修建的公路成环。如下图,A申请修建公路AB,B申请修建公路BC,C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请;

(3)其他情况的申请一律同意。
一轮修建结束后,可能会有若干城市可以通过公路直接或间接相连。这些可以互相:连通的城市即组成“城市联盟”。在下一轮修建中,每个“城市联盟”将被看作一个城市,发挥一个城市的作用。
当所有城市被组合成一个“城市联盟”时,修建工程也就完成了。
你的任务是根据城市的分布和前面讲到的规则,计算出将要修建的公路总长度。
输入格式
第一行一个整数n,表示城市的数量。(n≤5000)
以下n行,每行两个整数x和y,表示一个城市的坐标。(-1000000≤x,y≤1000000)
输出格式
一个实数,四舍五入保留两位小数,表示公路总长。(保证有惟一解)
输入输出样例
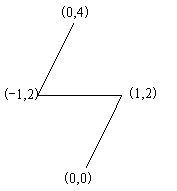
4 0 0 1 2 -1 2 0 4
6.47
说明/提示
修建的公路如图所示:
解析:
MST裸题(不接受挨打)
由于是稠密图,所以采用了Prim算法
(稀疏图最好用克鲁斯卡尔)
对任意两个点都求出距离
然后对其跑一遍最小生成树
但是注意n的范围是5000,而大小限制为125MB
题目本身不难,但是会一直MLE,所以需要优化
我这里有三个代码,不同的分数
第一个是裸的开 5000*5000 double数组的Prim算法可以跑出80分的好成绩(不开O2)。、
第二个是裸的克鲁斯卡尔算法,不开O2估计70分,开了O2稳定80分,运气好的话就是90分
第三个就是Prim,与第一个Prim不同的是会减少大量的冗余运算,具体体现就是把 5000 * 5000 的数组取消掉
只会在需要计算的时候才会计算,将大大减少时间和内存,,,所以就AC了。


1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<string> 6 #include<algorithm> 7 #include<iomanip> 8 #include<cstdlib> 9 #include<queue> 10 #include<set> 11 #include<map> 12 #include<stack> 13 #include<vector> 14 #define LL long long 15 #define re register 16 #define INF 0x7fffffff 17 #define Max 5002 18 #define D double 19 inline int read() 20 { 21 int s=0,f=-1;char ch=getchar(); 22 while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} 23 while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); 24 return s*f; 25 } 26 int n;D ans=0.0,g[Max][Max],dis[Max]; 27 bool vis[Max]={0}; 28 struct edge { 29 D x,y; 30 }t[Max]; 31 D Dis(D x1,D y1,D x2,D y2) 32 { 33 return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); 34 } 35 int main() 36 { 37 scanf("%d",&n); 38 for(re int i = 1 ; i <= n ; ++ i) g[i][i]=0,scanf("%lf%lf",&t[i].x,&t[i].y); 39 for(re int i = 1 ; i <= n ; ++ i) 40 for(re int j = i+1 ; j <= n ; ++ j) 41 g[i][j]=g[j][i]=Dis(t[i].x,t[i].y,t[j].x,t[j].y); 42 int pos;vis[1]=1; 43 for(re int i = 1 ; i <= n ; ++ i) dis[i]=g[1][i]; 44 for(re int i = 1 ; i < n ; ++ i) { 45 pos=0; 46 for(re int j = 1 ; j <= n ; ++ j) { 47 if(vis[j]==1) continue; 48 if(!pos || dis[j] < dis[pos]) pos=j; 49 } 50 vis[pos]=1; 51 ans+=dis[pos]; 52 for(re int j = 1 ; j <= n ; ++ j) { 53 if(vis[j]==1) continue; 54 dis[j]=std::min(dis[j],g[pos][j]); 55 } 56 } 57 printf("%.2lf",ans); 58 return 0; 59 }

1 // luogu-judger-enable-o2 2 #include<iostream> 3 #include<cstdio> 4 #include<cmath> 5 #include<cstring> 6 #include<string> 7 #include<algorithm> 8 #include<iomanip> 9 #include<cstdlib> 10 #include<queue> 11 #include<set> 12 #include<map> 13 #include<stack> 14 #include<vector> 15 #define LL long long 16 #define re register 17 #define Max 5000*5000/2 18 #define D double 19 inline int read() 20 { 21 int s=0,f=-1;char ch=getchar(); 22 while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} 23 while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); 24 return s*f; 25 } 26 int n,pa[Max];D ans=0; 27 struct edge { 28 D x,y; 29 }t[Max]; 30 struct DIS { 31 D dis; 32 int from,to; 33 friend bool operator<(DIS a,DIS b) { 34 return a.dis<b.dis; 35 } 36 }e[Max]; 37 int find(int x) 38 { 39 if(x!=pa[x]) pa[x]=find(pa[x]); 40 return pa[x]; 41 } 42 void join(int x,int y) 43 { 44 x=find(x);y=find(y); 45 pa[y]=x; 46 } 47 D Dis(D x1,D y1,D x2,D y2) 48 { 49 return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); 50 } 51 int main() 52 { 53 scanf("%d",&n);int cnt=0; 54 for(re int i = 1 ; i <= n ; ++ i) pa[i]=i,scanf("%lf%lf",&t[i].x,&t[i].y); 55 for(re int i = 1 ; i <= n ; ++ i) 56 for(re int j = i+1 ; j <= n ; ++ j) 57 e[++cnt].dis=Dis(t[i].x,t[i].y,t[j].x,t[j].y),e[cnt].from=i,e[cnt].to=j; 58 int k=0; 59 std::sort(e+1,e+1+cnt); 60 for(re int i = 1 ; i <= cnt ; ++ i) { 61 int x=e[i].from,y=e[i].to;D t=e[i].dis; 62 if(find(x)!=find(y)) join(x,y),ans+=t; 63 if(k==n-1) break; 64 } 65 printf("%.2lf",ans); 66 return 0; 67 }

1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<cstring> 5 #include<string> 6 #include<algorithm> 7 #include<iomanip> 8 #include<cstdlib> 9 #include<queue> 10 #include<set> 11 #include<map> 12 #include<stack> 13 #include<vector> 14 #define LL long long 15 #define re register 16 #define INF 0x7fffffff 17 #define Max 5002 18 #define D double 19 inline int read() 20 { 21 int s=0,f=-1;char ch=getchar(); 22 while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();} 23 while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); 24 return s*f; 25 } 26 int n;D ans=0.0,dis[Max]; 27 bool vis[Max]={0}; 28 struct edge {D x,y;}t[Max]; 29 D Dis(D x1,D y1,D x2,D y2){return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));} 30 int main() 31 { 32 scanf("%d",&n); 33 for(re int i = 1 ; i <= n ; ++ i) dis[i]=INF,scanf("%lf%lf",&t[i].x,&t[i].y); 34 int pos;dis[1]=0; 35 for(re int i = 1 ; i <= n ; ++ i) { 36 D m=INF*1.0; 37 for(re int j = 1 ; j <= n ; ++ j) 38 if(dis[j] < m && !vis[j]) m=dis[j],pos=j; 39 vis[pos]=1; 40 ans+=m; 41 for(re int j = 1 ; j <= n ; ++ j) { 42 if(vis[j]==1) continue; 43 D d=Dis(t[pos].x,t[pos].y,t[j].x,t[j].y); 44 dis[j]=std::min(dis[j],d); 45 } 46 } 47 printf("%.2lf",ans); 48 return 0; 49 }
