这篇教程发布仅天时间,就在Hacker News论坛上收获了574赞。程序员们纷纷夸赞这篇文章的代码写得很好,变量名很规范,让人一目了然。
下面就让我们一起从零开始学习神经网络吧。
实现方法搭建基本模块——神经元
在说神经网络之前,我们讨论一下神经元(Neurons),它是神经网络的基本单元。神经元先获得输入,然后执行某些数学运算后,再产生一个输出。比如一个2输入神经元的例子:

在这个神经元中,输入总共经历了3步数学运算,
先将两个输入乘以权重(weight):
x1→x1 × w1
x2→x2 × w2
把两个结果想加,再加上一个偏置(bias):
(x1 × w1)+(x2 × w2)+ b
最后将它们经过激活函数(activation function)处理得到输出:
y = f(x1 × w1 + x2 × w2 + b)
激活函数的作用是将无限制的输入转换为可预测形式的输出。一种常用的激活函数是sigmoid函数:
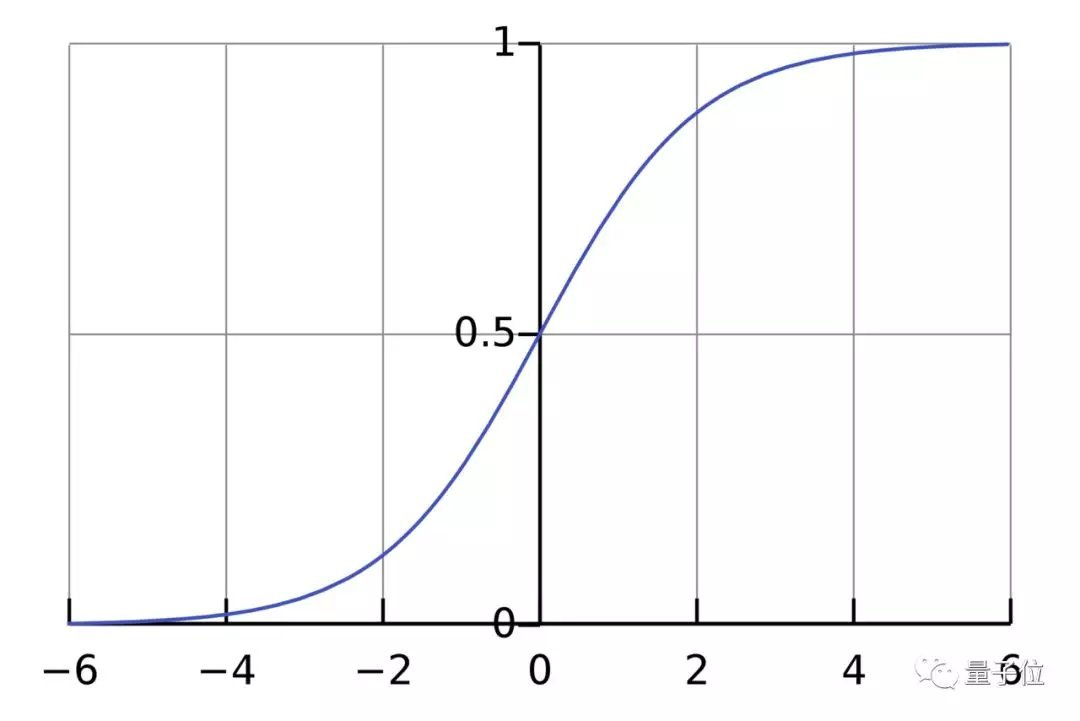
sigmoid函数的输出介于0和1,我们可以理解为它把 (−∞,+∞) 范围内的数压缩到 (0, 1)以内。正值越大输出越接近1,负向数值越大输出越接近0。
举个例子,上面神经元里的权重和偏置取如下数值:
w=[0,1]
b = 4
w=[0,1]是w1=0、w2=1的向量形式写法。给神经元一个输入x=[2,3],可以用向量点积的形式把神经元的输出计算出来:
w·x+b =(x1 × w1)+(x2 × w2)+ b = 0×2+1×3+4=7
y=f(w⋅X+b)=f(7)=0.999
以上步骤的Python代码是:
import numpy as np def sigmoid(x): # Our activation function: f(x) = 1 / (1 + e^(-x)) return 1 / (1 + np.exp(-x)) class Neuron: def __init__(self, weights, bias): self.weights = weights self.bias = bias def feedforward(self, inputs): # Weight inputs, add bias, then use the activation function total = np.dot(self.weights, inputs) + self.bias return sigmoid(total) weights = np.array([0, 1]) # w1 = 0, w2 = 1 bias = 4 # b = 4 n = Neuron(weights, bias) x = np.array([2, 3]) # x1 = 2, x2 = 3 print(n.feedforward(x)) # 0.9990889488055994
我们在代码中调用了一个强大的Python数学函数库NumPy。
搭建神经网络
神经网络就是把一堆神经元连接在一起,下面是一个神经网络的简单举例:

这个网络有2个输入、一个包含2个神经元的隐藏层(h1和h2)、包含1个神经元的输出层o1。
隐藏层是夹在输入输入层和输出层之间的部分,一个神经网络可以有多个隐藏层。
把神经元的输入向前传递获得输出的过程称为前馈(feedforward)。
我们假设上面的网络里所有神经元都具有相同的权重w=[0,1]和偏置b=0,激活函数都是sigmoid,那么我们会得到什么输出呢?
h1=h2=f(w⋅x+b)=f((0×2)+(1×3)+0)
=f(3)
=0.9526
o1=f(w⋅[h1,h2]+b)=f((0∗h1)+(1∗h2)+0)
=f(0.9526)
=0.7216
以下是实现代码:
import numpy as np # ... code from previous section here class OurNeuralNetwork: ''' A neural network with: - 2 inputs - a hidden layer with 2 neurons (h1, h2) - an output layer with 1 neuron (o1) Each neuron has the same weights and bias: - w = [0, 1] - b = 0 ''' def __init__(self): weights = np.array([0, 1]) bias = 0 # The Neuron class here is from the previous section self.h1 = Neuron(weights, bias) self.h2 = Neuron(weights, bias) self.o1 = Neuron(weights, bias) def feedforward(self, x): out_h1 = self.h1.feedforward(x) out_h2 = self.h2.feedforward(x) # The inputs for o1 are the outputs from h1 and h2 out_o1 = self.o1.feedforward(np.array([out_h1, out_h2])) return out_o1 network = OurNeuralNetwork() x = np.array([2, 3])