算术基本定理

内容：

 任何一个大于1的自然数N，都可以唯一分解成有限个质数的乘积 N=(P_1^a1)*(P_2^a2)......(P_n^an) , 这里P_1<P_2<...<P_n是质数，其诸方幂ai 是正整数。

这样的分解称为N 的标准分解式。

算术基本定理，又称为正整数的唯一分解定理，即：每个大于1的自然数均可写为质数的积，而且这些素因子按大小排列之后，写法仅有一种方式。例如:，。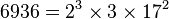

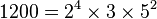算术基本定理的内容由两部分构成：

• 分解的存在性：
• 分解的唯一性，即若不考虑排列的顺序，正整数分解为素数乘积的方式是唯一的。

算术基本定理是初等数论中一个基本的定理，也是许多其他定理的逻辑支撑点和出发点。

证明：

算术基本定理的最早证明是由欧几里得给出的。准确的说，欧几里得证明了在一般整环上看与算术基本定理等价的命题：若质数，则不是 ，就是。然而，在欧几里得的时代，并没有发展出幂运算和指数的写法，甚至连四个整数的乘积这种算式都被认为是没有意义的，所以欧几里得并没有给出算术基本定理的现代陈述。

大于1的自然数必可写成素数之积

用反证法：假设存在大于1的自然数不能写成质数的乘积，把最小的那个称为n。

自然数可以根据其可除性（是否能表示成两个不是自身的自然数的乘积）分成3类：质数、合数和1。首先，按照定义，n 大于1。其次，n 不是质数，因为质数p可以写成质数乘积：p=p，这与假设不相符合。因此n只能是合数，但每个合数都可以分解成两个严格小于自身而大于1的自然数的积。设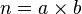，其中a 和b 都是介于1和n 之间的自然数，因此，按照n 的定义，a 和b 都可以写成质数的乘积。从而 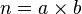也可以写成质数的乘积。由此产生矛盾。因此大于1的自然数必可写成质数的乘积。

唯一性

引理：若质数，则不是 ，就是。

引理的证明：若 则证明完毕。若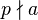，那么两者的最大公约数为1。根据裴蜀定理，存在 使得。于是。 由于，上式右边两项都可以被p整除。所以。

再用反证法：假设有些大于1的自然数可以以多于一种的方式写成多个质数的乘积，那么假设n 是最小的一个。

首先n 不是质数。将n 用两种方法写出： 。根据引理，质数 ，所以 中有一个能被整除，不妨设为。但也是质数，因此 。所以，比n小的正整数也可以写成 。这与n 的最小性矛盾！

因此唯一性得证。

转自：http://zh.wikipedia.org/wiki/%E7%AE%97%E6%9C%AF%E5%9F%BA%E6%9C%AC%E5%AE%9A%E7%90%86

应用：

（1）一个大于1的正整数N，如果它的标准分解式为： N=(P_1^a1)*(P_2^a2)......(P_n^an)

那么它的正因数个数为（1+a1)(1+a2).....(1+an)。

（2） 它的全体正因数之和为d(N)=(1+p_1+...p_1^an)(1+p_2+...p_2^a2)...(1+p_n+...+p_n^an)

当d(N)=2N时就称N为完全数。 是否存在奇完全数，是一个至今未解决之猜想。

（3） 利用算术基本定理可以重新定义整数a和b的最大公因子（a,b）和最小公倍数[a,b], 并证明ab=(a,b)[a,b].

 

  在第2章中讨论了两个数的最大公约数gcd (a, b)。现在我们可以回忆一下Euclidean算法给出这个值的方法。不过，如果我们已经知道a和b的因数分解结果，也可以不用Euclidean算法，直接用a和b的因数分解结果求出这个值。

 

2. 最小公倍数

最小公倍数lcm (a, b)，就是a和b的所有公倍数中的最小整数。运用因数分解，我们也能求出lcm (a, b)。

如下所示，我们可以证明gcd (a, b)和lcm (a, b)是相互联系的。

 

 

（4）此外还可证明根号2是无理数等等（毕达哥拉斯）。

（5） 证明素数个数无限。

http://baike.baidu.com/view/651164.htm