在一个8×8国际象棋盘上,有8个皇后,每个皇后占一格;要求皇后间不会出现相互“攻击”的现象,即不能有两个皇后处在同一行、同一列或同一对角线上。问共有多少种不同的方法。
我们用回溯法,现在的目的不是找有多少种解法,而是只要找出一种合适的解法输出即可。
先写一个place函数,判断当前位置是否合法:
bool place(int x[],int k) { int i; for(i=1;i<k;i++) if((x[i]==x[k])||(abs(x[i]-x[k])==abs(i-k))) return false; return true; }
这个函数以解向量x[]和皇后的行号k做参数,判断第k个皇后当前的列位置x[k]是否满足关系式,这样,他必须和第1~k-1行的所有皇后位置进行比较。
n皇后算法如下:
/* n 后问题 输入:皇后个数n 输出: n后问题的解向量 */ void n_queens(int n,int x[]) { int k=1; //x[0]不要 x[1]=0; while(k>0) { x[k]=x[k]+1; //在当前列加1的位置开始搜索,这句很重要 while(x[k]<=n&&(!place(x,k))) //当前列是否满足条件 x[k]=x[k]+1; if(x[k]<=n) //存在满足条件的列 { if(k==n) break; //是最后一个皇后,完成搜索 else { k=k+1; x[k]=0; //不是,处理下一个皇后 } } else //已判断完n列,均没有满足条件 { x[k]=0; k=k-1; //第k行复位为0,回溯到前一行 ,前一行列加1 x[k]=x[k]+1 } }//end while }
最后else {x[k]=0;不要可不可以,基本可以,为什么?
假设a[3]=0;k=3-1=2;
下一次轮到k=3; x[k]=0;
只有一种一种情况有点影响。
当没有解时x[1]没有置0,此时x[1]=n+1;退出while循环。
上面的代码有很多注意的地方。
如判断条件为什么是while(k>0)
假设有4个皇后。
仔细想想,假设当k=1此时a[k]=4;
a[k]还是不满足!place(x,k)))
a[k]=5;
就执行
else
{
x[1]=0;
k--;
}
k=0;
退出while循环,
说明已经把a[1]的所有可能值遍历完了,还是找不到条件满足。即没有找到解。
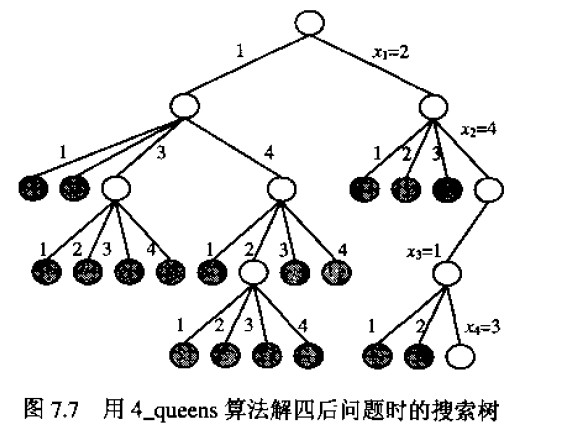
n=4搜索树:
main函数如下:
int main() { int n; cout<<"请输入皇后的数"; cin>>n; int *a=new int[n+2]; n_queens(n,a); cout<<"解向量为"<<endl; for(int i=1;i<=n;i++) cout<<a[i]<<ends; cout<<endl; for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) { if(j==a[i]) cout<<"* "<<ends; //要在*后留一个空格,口字占2格 else cout<<"口"<<ends; } cout<<endl; } }
输出全部的解:
添加一个count全局变量,赋值为0.然后只要修改增加下面的红色代码即可。
if(a[k]<=n) { if(k==n) //是最后一个皇后,完成搜索 { count++; output(a,n); //a[k]=0; 要不要,都可以,原因同前面的一样. k--; } else { k++; a[k]=0; } }
用递归求解有:
解向量 (x1,x2,......xn)
显约束 xi=1,2.....n
隐约束:
1)不同列 xi!=xj
2)不出来同一正,反对角线 |i-j|!=|xi-xj|
#include<iostream> #include<cstdlib> using namespace std; #define NumQueen 8 int queen[NumQueen]; int sum=0; //解决方案总数 8后有92组解 void display() { int i,j; cout<<"第"<<sum+1<<"个解决方案-->"; for(i=0;i<NumQueen;i++) { for(j=0;j<NumQueen;j++) if(queen[i]==j) cout<<"("<<i+1<<","<<queen[i]+1<<")"; } cout<<endl; sum++;//解的组数 } bool check(int k) { int i; for(i=0;i<k;i++) if((queen[i]==queen[k])||(abs(queen[i]-queen[k])==abs(i-k))) return false; return true; } void putQueen(int k) { int i; for(i=0;i<NumQueen;i++) { queen[k]=i; if(check(k)) { if(k==NumQueen-1) display(); else putQueen(k+1); } } } int main() { cout<<"方按,其中(行标,列标)为皇后的位置\n\n"; putQueen(0); cout<<"\n共有"<<sum<<"个方案\n"; }
怎么理解上面递归的代码?
上面k=0开始,我们也可以从k=1开始。
对照这幅图理解;

、f(1) for(i=1) a[1]=1; 调用f(2)
f(2) for(int i=1 check(a,1)不满足条件,i=2;a[2]=2;不满足条件i=3,a[2]=3,满足 调用f(3)
f(3) for循环完成后
check(a,k)还是不满足退出。
注意是f(2)调用f(3)的,f(3)完成退出后,由于没有进入
下一次递归,于是就再次运行(这是算法的关键点)
for(i=1;i<=n;i++)
{
a[k]=i;
..
}
由于上次i=3,这次i=4 a[2]=4.
还有一点要理解,上面的代码为什么会输出全部的解?
原因还是跟上面的一样,
if(k==NumQueen-1) display(); else putQueen(k+1);
输出完成后没有进入下一次递归,又进入了下一次循环。
程序是怎么退出的,可以从整体理解。
f(1)时for循环内a[i]=n+1就退出了。
问?递归代码怎么只输出一个解?
最开始我们尝试在
if(k==NumQueen-1) display();
后面加个break;
但是不起作用,还是输出了全部解。
输出全部解自己写的代码:
void nQueens4(int a[],int n,int k) { int i; for(int i=1;i<=n;i++) { a[k]=i; if(check(a,k)) { if(k==n) { count++; output(a,n); } else { nQueens4(a,n,k+1); } } } }
上面的代码和下面的一样:
void nQueens5(int a[],int n,int k) { if(k>n ) {count++;output(a,n);} else { for(int i=1;i<=n;i++) { a[k]=i; if(check(a,k)) { nQueens5(a,n,k+1); } } } }
你知道为什么吗?(第二种方式用的比较多)