前言
在做并查集的题目时,有的时候会遇到数据范围远大于数据个数的情况,这时候用普通的并查集就会导致MLE,例如下图:
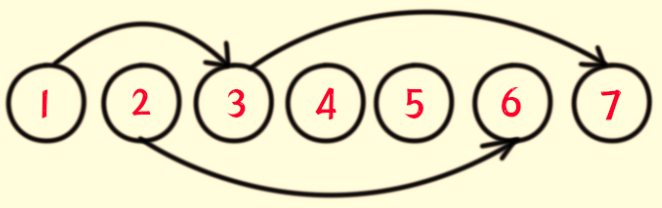
数据范围是1-7,但是只有5个节点,其中4,5节点并不在数据中,但是建立数组时,却也要建立大小等于数据范围大小(7)
的数组,当差距小时不明显,如果差距过大,就会导致严重的空间浪费,这时候,就要用离散化来解决.
基于map的离散化
这道题i,j的数据范围是[1,1e9],显然不能建这么大的并查集数组,该怎么离散化呢?
我觉得这道题用map离散化比较好.
map介绍
先介绍一下map:
使用map时,首先包含头文件
#include<map>
定义时:
map<键数据类型,值数据类型> 名称;
例如
map<int,int> m;
表示定义一个int-int的map
使用时可以像数组一样使用下标赋值或获取值,当map中不存在此键时,会返回广义上的空,否则返回键所对应的值.
注意,即使map不存在键,返回空,但map中却会建立起一个键-空的关系,这个空值不会删除,所以必须处理好,否则会拖慢速度.
可以使用map.find(key) == map.end()来判断map中是否有key这个键,当表达式为真,不存在,当表达式为假,存在.
离散化
离散化的核心思想就是建立对应关系,对每一个值给一个编号,这个编号不像值可能是断断续续的,编号是连续的,
再看一下这个图:

值 编号
1 1
2 2
3 3
6 4
7 5
然后对编号操作即可
代码:
#include <cstdio>
#include <iostream>
#include <map>
#include <vector>
using namespace std;
int t, n, x, y, e, fa[200005], flag, cnt, pcnt;
struct P{int a,b;}p[1000005];
map<int, int> m;
int find(int x) { return fa[x] == x ? x : (fa[x] = find(fa[x])); }
void join(int x, int y) { fa[find(x)] = find(y); }
bool in_one(int x, int y) { return find(x) == find(y); }
int main() {
scanf("%d", &t);
while (t--) {
m.clear();
flag = cnt = pcnt = 0;
scanf("%d", &n);
for (int i = 1; i <= 2 * n; ++i) fa[i] = i;
for (int i = 1; i <= n; ++i) {
scanf("%d%d%d", &x, &y, &e);
if (m.find(x) != m.end()) // 当已经存在map中.说明已经分配了编号
x = m[x]; //m[x]就是x的编号
else {
m[x] = ++cnt; //分配一个编号
x = cnt;
}
if (m.find(y) != m.end()) //对y进行相同操作
y = m[y];
else {
m[y] = ++cnt;
y = cnt;
}
if (e)
join(x, y);
else {
p[pcnt].a=x;
p[pcnt++].b=y;
}
}
for (int i=0;i<pcnt;i++) {
if (find(p[i].a) == find(p[i].b)) {
printf("NO
");
goto end;
}
}
printf("YES
");
end:1;
}
return 0;
}
这道题只需要回答是否符合条件,光使用编号运算就够了,那么如果算完之后还需要输出原数据呢?
基于排序,去重和二分的离散化
(碎碎念:这篇文章本来是老姚让我分享给同学的,结果写到这里虎哥突然发了离散化的课件,就不用分享了...然后下面的内容差不多都是抄的虎哥的)
unique函数
对某个区间(作为参数传入)的数据进行去重,返回去重的结果序列的最后一个元素的下一个指针
用下标解释:若去重后,不重复的元素有5个,假设最后一个元素的下标为5,则该函数返回6
例如有8个数:2 1 2 4 1 4 3 5
假设下标从1开始,即每个元素的地址分别为&a[1],&a[2] … &a[8]
要对整个数列去重,可以调用函数unique(a+1, a+1+8),去重后有效数据为2 1 4 3 5,分别存在[1], a[2] … a[5]里面,函数的返回值为指向a[5]的后面一个元素的指针,即&a[6]。因此我们要求不重复的元素的个数,需要:
int size = unique(a+1, a+1+8) – (a+1)
此时size存的值即为去重后不相同元素的个数。
lower_bound函数
返回某个区间内第一个不小于查询的关键字key的元素的指针。
例如有5个数:0 1 2 3 4,如果在a[1]到a[5]这个区间查找数值3的lower_bound,则调用lower_bound(a+1, a+1+5, 3),则返回值为a[4]的地址,即&a[4],如果我们要得到它对应的下标,需要用返回值减去该数组的首地址,即:int k = lower_bound(a+1, a+1+5, 3) – a;
假设原数据存在a[i]数组里,b[i]为a[i]的一个副本(b与a相同)
std::sort(a + 1, a + 1 + n);
int size = std::unique(a + 1, a + 1 + n) – (a + 1);
int k;
for (int i = 1; i <= n; ++i){
k = std::lower_bound(a + 1, a + 1 + size, b[i]) - a;
printf("%d ", k);
k = std::upper_bound(a + 1, a + 1 + size, b[i]) - a;
printf("%d
", k);
}