题目
In a village called Byteville, there are (n) houses connected with (n-1) roads.
For each pair of houses, there is a unique way to get from one to another.
The houses are numbered from (1) to (n).
The house no. 1 belongs to the village administrator Byteasar.
As part of enabling modern technologies for rural areas framework, nn computers have been delivered to Byteasar's house.
Every house is to be supplied with a computer, and it is Byteasar's task to distribute them.
The citizens of Byteville have already agreed to play the most recent version of FarmCraft (the game) as soon as they have their computers.
Byteasar has loaded all the computers on his pickup truck and is about to set out to deliver the goods.
He has just the right amount of gasoline to drive each road twice.
In each house, Byteasar leaves one computer, and immediately continues on his route.
In each house, as soon as house dwellers get their computer, they turn it on and install FarmCraft.
The time it takes to install and set up the game very much depends on one's tech savviness, which is fortunately known for each household.
After he delivers all the computers, Byteasar will come back to his house and install the game on his computer.
The travel time along each road linking two houses is exactly 1 minute, and (due to citizens' eagerness to play) the time to unload a computer is negligible.
Help Byteasar in determining a delivery order that allows all Byteville's citizens (including Byteasar) to start playing together as soon as possible.
In other words, find an order that minimizes the time when everyone has FarmCraft installed.
在一个叫做比特村的小村庄中,有(n-1)条路连接着这个村庄中的全部nn个房子。
每两个房子之间都有一条唯一的通路。这些房子的编号为(1)至(n)。
1号房子属于村庄的管理员比特安萨尔。
为了提升村庄的科技使用水平,(n)台电脑被快递到了比特安萨尔的房子。每个房子都应该有一台电脑,且分发电脑的任务就落在了比特安萨尔的肩上。
比特村的居民一致同意去玩农场物语这个游戏的最新快照版,而且好消息是他们很快就要得到他们最新的高配置电脑了。
比特安萨尔将所有电脑都装在了他的卡车上,而且他准备好完成这个艰巨的任务了。
他的汽油恰好够走每条路两遍。
在每个房子边,比特安萨尔把电脑贴心的配送给居民,且立即前往下一个房子。(配送过程不花费任何时间)
只要每间房子的居民拿到了他们的新电脑,它们就会立即开始安装农场物语。安装农场物语所用的时间根据居民的科技素养而定。幸运的是,每间房子中居民的科技素养都是已知的。
在比特安萨尔配送完所有电脑后,他会回到他自己的1号房子去安装他自己的农场物语。
用卡车开过每条路的时间恰好是1分钟,而居民开电脑箱的时间可以忽略不计。(因为他们太想玩农场物语了)
请你帮助比特安萨尔算出从开始配送到所有居民都玩上了农场物语的最少时间。
输入格式
The first line of the standard input contains a single integer (n(2le nle 500 000)) that gives the number of houses in Byteville.
The second line contains (n) integers (c_1,c_2,cdots,c_n(1le c_ile 10^9)),separated by single spaces; (c_i) is the installation time (in minutes) for the dwellers of house no. i.
The next (n-1) lines specify the roads linking the houses.
Each such line contains two positive integers aa and (b (1le a<ble n)), separated by a single space.These indicate that there is a direct road between the houses no. aa and bb.
第一行包含一个整数(n(2 leq n leq 500000)),代表比特村中有多少房子。
第二行包含nn个整数(c_1, c_2, ⋯, c_n(1 leq c_i leq 10^9)),每个数都被单个空格隔开。(c_i)是第i号房间中居民安装农场物语所用的时间。
接下来的n-1n−1行代表了每一条路的两个顶点。两个顶点(a)和(b)满足((1 leq a < b leq n)),两个数之间有一个空格。
输出格式
The first and only line of the standard output should contain a single integer:
the (minimum) number of minutes after which all citizens will be able to play FarmCraft together.
一行,包含一个整数,代表题目中所说的最小时间。
输入样例
6
1 8 9 6 3 2
1 3
2 3
3 4
4 5
4 6
输出样例
11
样例解释
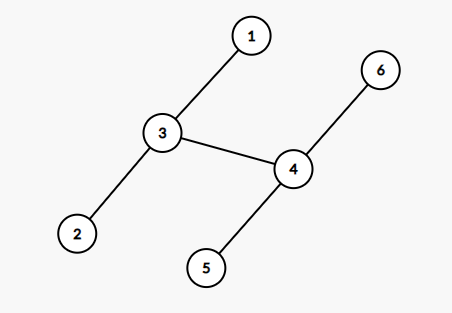
题解
前几天刚写过salesman,一看这题就觉得有点相似,主要是DFS的过程相似
对于一棵子树的根节点来说,已知遍历时间和装软件时间,我们该怎么分配遍历的顺序?
首先明确,要输出的答案是遍历所有子树且所有子树安装好软件的时间,那么,有没有可能比特安萨尔已经遍历完成,但是因为某些技术水平不高的居民而不得不继续等待耗费时间的情况?有可能,那么为了尽可能减少这个时间,我就先遍历那些技术水平不高的居民.
注意,如果安装时间最长,但需要遍历的时间也很长,不一定需要先遍历,因为遍历是一定需要遍历的,这些时间不能节省,遍历是比特安萨尔去遍历,一个人同时只能干一件事情,但安装是居民安装,可以同时多个居民同时安装.
如果本来可以同时安装但我让他尽可能多地同时安装,就会浪费时间.
所以我们应该先遍历的是总时间减遍历时间最大的,这些时间就是从DFS完成,回溯开始到软件安装完成的时间.这些时间可以用来遍历别的子树.
看一下这个图:

每一行代表一个居民的时间分配.
黄色是遍历时间,蓝色是安装时间.黄色首尾相接代表只能同时遍历一棵子树,蓝色可以重叠表示居民可以同时安装,
上面一块是没有优化的版本,可以看出来4号居民的安装时间大大拖慢了总体时间
下面是优化过的,可以看出来4号居民长长的安装时间是和遍历同时进行的,没有拖慢时间.
所以更新子树时,根据总时间减遍历时间从大到小排序即可.
代码
#include <algorithm>
#include <cstdio>
using namespace std;
const int maxn = 500001;
struct Edge {
int to, next;
} edges[maxn<<1];
int n, head[maxn], cnt, u, v, a[maxn], dp[maxn], dis[maxn], son[maxn];
bool cmp(int x, int y) { return dp[x] - dis[x] > dp[y] - dis[y]; }
void add(int u, int v) { edges[++cnt].to = v, edges[cnt].next = head[u], head[u] = cnt; }
void dfs(int root, int fa) {
if (root != 1) dp[root] = a[root];
for (int i = head[root]; i; i = edges[i].next)
if (edges[i].to != fa) dfs(edges[i].to, root);
int sonn = 0;
for (int x = head[root]; x; x = edges[x].next)
if (edges[x].to != fa) son[++sonn] = edges[x].to;
sort(son + 1, son + sonn + 1, cmp);
for (int i = 1; i <= sonn; ++i)
dp[root] = max(dp[root], dp[son[i]] + dis[root] + 1), dis[root] += dis[son[i]] + 2;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
for (int i = 1; i < n; ++i) {
scanf("%d%d", &u, &v);
add(u, v);
add(v, u);
}
dfs(1, 0);
printf("%d
", max(dp[1], dis[1] + a[1]));
return 0;
}