树论基础部分在以前学习数组链表时有简单了解,二叉树遍历没有学习过,这里跟着子龙老师学习下二叉树遍历,最后再学习归并排序。
树形结构
树是数据结构与算法中一种非常重要的结构,是由N个具有层次的结点组成,其具有以下特点:
(1)有一个根结点,一般称为root结点
(2)每一个元素称为node
(3)除了root结点外,其余结点会被分为n个互不相交的集合,即n个互不相交的子树
树形结构基本名词:
(1)结点:node,树形结构里的基本元素
(2)子树:除了root结点外,其余结点会被分为互不相交的子树
(3)度:一个结点拥有子树的数量称为结点的度
(4)叶子:度为0的结点
(5)深度:结点的最大层次称为深度,计算时间复杂度使用
(6)森林:由N个互不相交的树组成森林

如图所示就是树结构,顶部就是root结点,下面有三个子树,因此根结点的度为3,并且从结点的层次可以得到上面树结构的深度为3。
二叉树
二叉树就是一种特殊的树形结构,其每个结点最大的度就是2,在二叉树的第n层上之多有2^(n-1)个结点,总共最多有2^n-1个结点,如果是满二叉树,则结点数就是2^n-1。具有n个结点的满二叉树,其深度为log2^(n+1),这个特性决定了索引树的时间复杂度。
可以简单的推导一下,从根节点开始,到第n层,依次为2^0个,2^1个,...,2^(n-1)个,相加就是s=2^0+2^1+...+2^(n-1),乘2变成2s=2^1+2^2+...+2^n,2s-s相减得到s=2^n-1。如果是n个结点的满二叉树计算深度,可以假设深度为x,这样2^x-1=n,然后得到2^x=n+1,最后得到深度x=log2^(n+1)。
二叉树的遍历
下面是二叉树的遍历,为了更好的理解,先画一个图来准备二叉树遍历描述,如下所示。
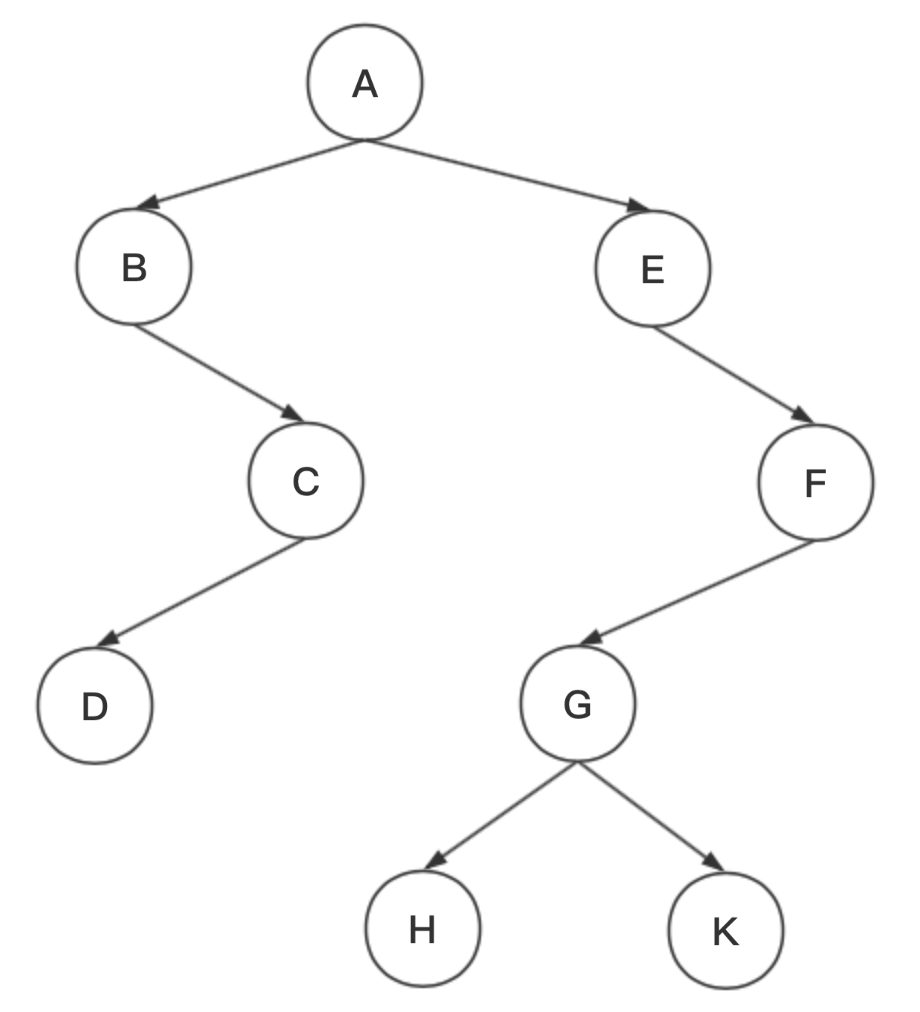
(1)前序遍历:根结点→左子树→右子树
以上面图为例,到根结点就输出,然后遍历左子树和右子树,将左子树和右子树的结点作为新的根结点继续进行同样的遍历操作。
1 首先从根结点A进入,因此先输出A
2 然后进入左子树,将结点B作为新的根结点,因此输出B,然后寻找B结点的左子树发现没有跳过,再寻找右子树找到C结点
3 将C结点作为根结点,因此输出C,然后进入左子树,发现有左子树并找到D结点
4 将D结点作为根结点,因此输出D,然后寻找D的左子树发现没有,然后右子树也发现没有,因此左边这根大子树遍历完了,准备遍历右子树
5 将E结点作为根结点,因此输出E,然后寻找E的左子树发现没有,然后寻找右子树发现F结点
6 将F结点作为根节点,因此输出F,然后寻找F的左子树发现G
7 将G结点作为根节点,因此输出G,然后寻找G的左子树发现H
8 将H结点作为根节点,因此输出H,然后寻找H的左子树发现没有,再寻找H的右子树也发现没有,然后跳到G的右子树发现K结点
9 将K结点作为根节点,因此输出K,然后寻找K的左子树发现没有,再寻找K的右子树发现没有,最后遍历完了
因此最后将输出ABCDEFGHK。
(2)中序遍历:左子树→根结点→右子树

无论哪个结点,首先遍历当前结点左边子树,遍历完后输出当前根节点,然后再遍历右边子树,每个子树的起始结点又作为新的根结点,继续执行前面同样的逻辑。
1 从根节点A进入,首先遍历左子树,因此先进入B结点开始的左子树,将B作为左子树的根结点,先寻找B的左子树,发现没有因此遍历完成回到B,因此输出B,然后进入B结点右子树,发现C结点
2 将C结点作为新的子树根结点,先寻找C的左子树,发现D结点
3 将D结点作为新的子树根结点,先寻找D的左子树,发现没有,因此回到根结点输出D,然后寻找D的右子树发现没有,D结点开始的左子树遍历完成,然后进入上面根结点输出C,继续寻找C的右结点发现没有,这样以A结点为根的左子树遍历完成,进入根A结点,因此输出A,并进入右子树找到E结点
3 将E结点作为新的子树根结点,先寻找E结点的左子树,发现没有然后回到E结点,因此输出E,然后寻找E结点的右子树发现F结点
4 将F结点作为新的子树根结点,先寻找F结点的左子树,发现G结点
5 将G结点作为新的子树根结点,先寻找G的左子树,发现H结点
6 将H结点作为新的子树根结点,先寻找H的左子树发现没有,回到H,因此输出H,然后寻找H的右子树发现没有,因此以G为根结点的左子树遍历完成回到G结点,输出G,然后寻找G结点的右子树发现K结点
7 将K结点作为新的子树根结点,先寻找K的左子树发现没有,回到K,因此输出K,然后寻找K的右子树没有,这样以F为根结点的左子树遍历完了,再回到F结点,因此输出F,在寻找F的右子树,发现没有,这样全部遍历完成
因此最后将输出BDCAEHGKF。
(3)后序遍历:左子树→右子树→根结点

后续遍历,先从结点左子树开始,左子树遍历完进入右子树,右子树遍历完后再进入上层根结点,每个结点都按照这个逻辑来遍历。
1 从根节点A进入后,先进入左子树,发现B结点
2 以B结点作为当前根结点,继续进入左子树,发现没有,然后进入右子树发现C结点
3 以C结点作为当前根结点,继续进入左子树,发现D结点
4 以D结点作为当前根结点,继续进入左子树发现没有,然后进入右子树发现没有,这样继续回到当前根结点D,因此输出D,这样以C结点为根结点的左子树遍历完了,继续寻找C的右子树
5 C的右子树没有因此回到C结点,输出C,这样以B结点为根结点的右子树遍历完成,回到B结点输出B,这样以根结点A的左子树遍历完成,进入A的右子树发现E结点
6 以E结点作为当前根结点,继续寻找E的左子树发现没有,然后寻找E的右子树发现F结点
7 以F结点作为当前根结点,继续寻找左子树发现G结点
8 以G结点为当前根结点,继续寻找左子树发现H结点
9 以H结点为当前根结点,继续寻找左子树发现没有,然后寻找右子树发现没有,回到H结点输出H,然后进入G结点为根结点的右子树,找到K结点
10 以K结点为当前根结点,继续寻找左子树发现没有,然后寻找右子树发现没有,回到K结点输出K,然后回到上层G根结点,输出G,这样以F结点为根结点的左子树遍历完成,寻找F的右子树发现没有,再回到F结点输出F
11 以E结点为当前根结点右子树遍历完成,回到E结点因此输出E,然后以A结点为根结点的右子树遍历完了,回到根结点A并输出A
因此最后将输出DCBHKGFEA。
以下为二叉树遍历代码实现,定义的node类,包括数据部分,还有左子结点和右子结点。
1 //代表结点node 2 class Node{ 3 private char data;//代表字母 4 private Node leftNode;//左边node 5 private Node rightNode;//右边node 6 //构造方法 7 public Node(char data, Node leftNode, Node rightNode) { 8 super(); 9 this.data = data; 10 this.leftNode = leftNode; 11 this.rightNode = rightNode; 12 } 13 //get set方法 14 public char getData() { 15 return data; 16 } 17 18 public void setData(char data) { 19 this.data = data; 20 } 21 22 public Node getLeftNode() { 23 return leftNode; 24 } 25 26 public void setLeftNode(Node leftNode) { 27 this.leftNode = leftNode; 28 } 29 30 public Node getRightNode() { 31 return rightNode; 32 } 33 34 public void setRightNode(Node rightNode) { 35 this.rightNode = rightNode; 36 } 37 } 38 /** 39 * 二叉树遍历 40 */ 41 public class BinaryTree { 42 43 //输出方法 44 public static void print(Node node){ 45 System.out.print(node.getData()); 46 } 47 48 //前序遍历 根结点→左子树→右子树 49 public void pre(Node root){ 50 print(root); 51 if(root.getLeftNode()!=null){ 52 pre(root.getLeftNode()); 53 } 54 if(root.getRightNode()!=null){ 55 pre(root.getRightNode()); 56 } 57 } 58 //中序遍历 左子树→根结点→右子树 59 public void in(Node root){ 60 if(root.getLeftNode()!=null){ 61 in(root.getLeftNode()); 62 } 63 print(root); 64 if(root.getRightNode()!=null){ 65 in(root.getRightNode()); 66 } 67 } 68 //后续遍历 左子树→右子树→根结点 69 public void post(Node root){ 70 if(root.getLeftNode()!=null){ 71 post(root.getLeftNode()); 72 } 73 if(root.getRightNode()!=null){ 74 post(root.getRightNode()); 75 } 76 print(root); 77 } 78 79 public static void main(String[] args) { 80 //初始化树结构数据 81 Node D=new Node('D',null,null); 82 Node H=new Node('H',null,null); 83 Node K=new Node('K',null,null); 84 Node C=new Node('C',D,null); 85 Node B=new Node('B',null,C); 86 Node G=new Node('G',H,K); 87 Node F=new Node('F',G,null); 88 Node E=new Node('E',null,F); 89 Node A=new Node('A',B,E); 90 91 //调用前序遍历 92 BinaryTree tree=new BinaryTree(); 93 System.out.println("前序遍历"); 94 tree.pre(A); 95 System.out.println(); 96 97 //中序遍历 98 System.out.println("中序遍历"); 99 tree.in(A); 100 System.out.println(); 101 102 //后续遍历 103 System.out.println("后序遍历"); 104 tree.post(A); 105 106 } 107 }
控制台输出结果,可以看出跟上面的分析一致,因此文中代码也是一种实现二叉树遍历的方式。

归并排序
归并排序起源于1945年,由冯-诺依曼首次提出,是一种仅次于快速排序的排序方法。归并排序体现了两个部分,一个是分的过程一个是合的过程,核心思想是将两个已经有序的数组再合并成一个大的有序数组。如下图是归并的一个过程。上面蓝色部分代表归,即拆分,下面黄色部分代表并,即排序后和并。因此需要用代码分别实现二分拆分的过程,以及后面的和并过程,个人感觉这一部分很难直观的理解,因此代码中实行打桩,加上后面做了一个图来更好的理解拆和并的过程。
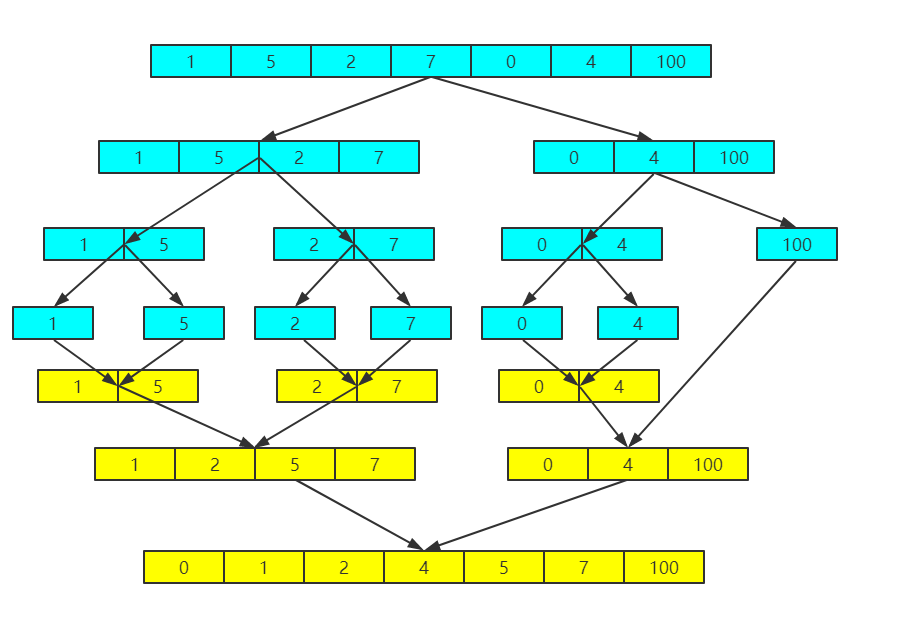
以下为代码实现,拆的过程结合后面的图能能更好的理解,进入方法代码执行到拆分左子树时代码时,继续往下拆分为左子树和右子树,并根据索引下标判断是否继续拆分,如此循环,直到拆分到下标相同,就打印出"左边分好了"或者"右边分好了"。这个过程跟遍历二叉树有点类似,打印出提示信息类似打印出根结点内容,只是这里打印的时机是在执行完一个对左子树的完全二分,以及对右子树的完全二分后。
1 import java.util.Arrays; 2 3 /** 4 * 归并排序 5 */ 6 public class MergeSort { 7 8 public static void main(String[] args) { 9 int[] data=new int[]{1,5,2,7,0,4,100}; 10 mergeSort(data,0,data.length-1); 11 //打印输出 12 System.out.println(Arrays.toString(data)); 13 } 14 15 //拆分,按照中间索引位置分为左边部分和右边部分,拆分完后进行合并 16 public static void mergeSort(int[] data,int left,int right){ 17 if(left<right){ 18 19 int mid=(left+right)/2; 20 System.out.println(mid); 21 22 //左边继续拆分,递归 23 mergeSort(data,left,mid); 24 System.out.println("左边分好了"); 25 26 //右边继续拆分,递归 27 mergeSort(data,mid+1,right); 28 System.out.println("右边分好了"); 29 30 //左右拆分完成和进行合并 31 merge(data,left,mid,right); 32 } 33 } 34 35 36 /** 37 * 比较左右子树并进行合并 38 * @param data 传入的数组 39 * @param left 左子树的最左边索引 40 * @param mid 拆分位置的索引 41 * @param right 右子树的最右边索引 42 */ 43 public static void merge(int[] data,int left,int mid,int right){ 44 int[] tmp=new int[data.length];//临时存储比较后的数字 45 int loc=left;//存进去临时数组的起始位置,从left开始 46 int point1=left;//左子树的起始位置 47 int point2=mid+1;//右子树的起始位置 48 //左右子树开始轮流取值比较,将更小的放到临时数组里去 49 while(point1<=mid&&point2<=right){ 50 if(data[point1]<data[point2]){ 51 tmp[loc]=data[point1]; 52 loc++; 53 point1++; 54 }else{ 55 tmp[loc]=data[point2]; 56 loc++; 57 point2++; 58 } 59 } 60 //上面比较完后最理想情况是左右子树所有的数都放到了临时数组,但是实际情况不是这么完美的,总会有一个子树会多留一点数据 61 //多留的一部分数据直接加到临时数组的后面 62 while (point1<=mid) { 63 tmp[loc++]=data[point1++]; 64 } 65 while(point2<=right){ 66 tmp[loc++]=data[point2++]; 67 } 68 //最后将临时数组按照索引一一更新到原数组中 69 for (int i = left; i <=right; i++) { 70 data[i]=tmp[i]; 71 } 72 } 73 }
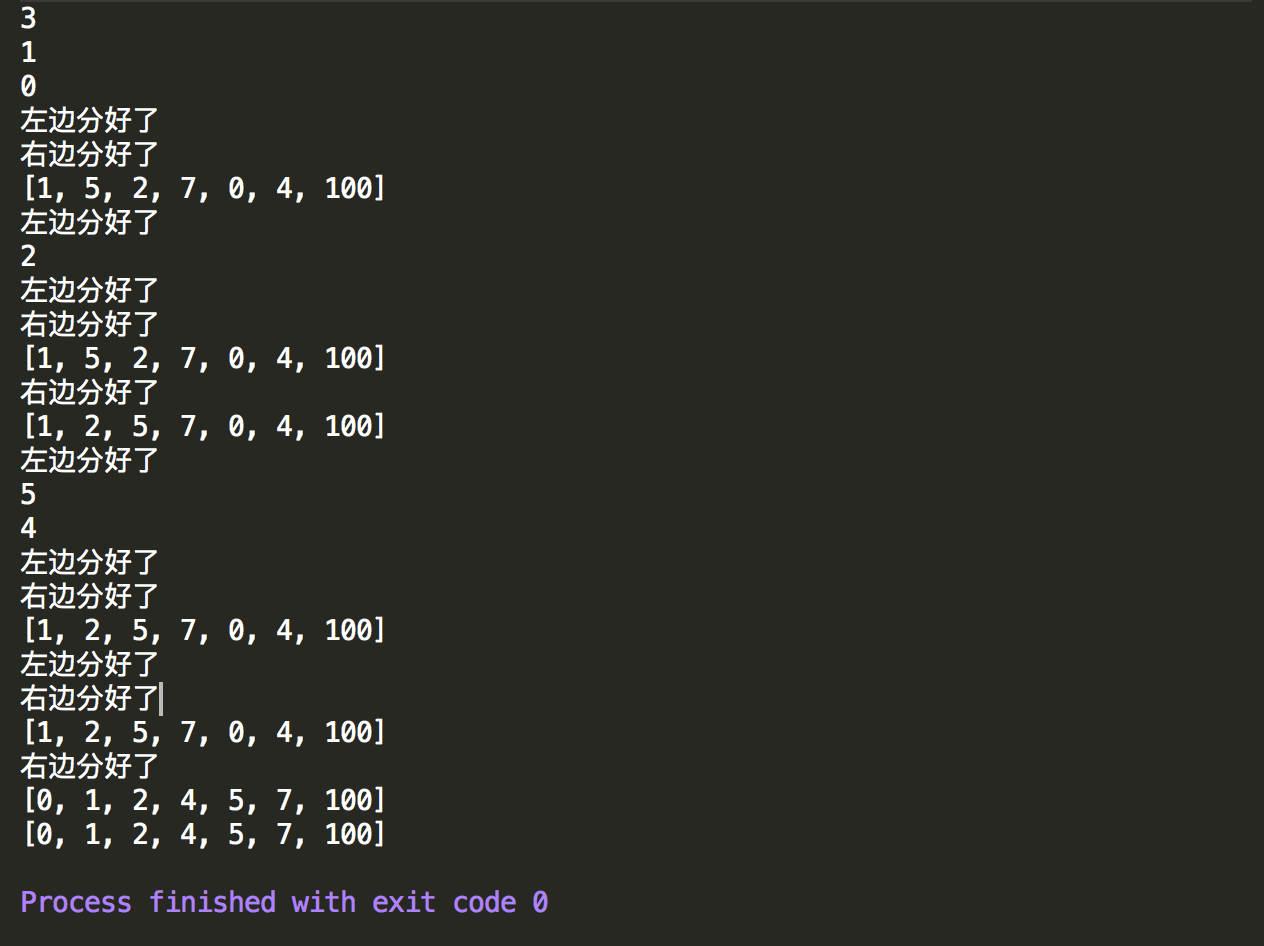
控制台输出结果如下图,可以看出能正确的进行排序,其中控制台输出的二分下标,以及打桩的文字为啥按照这样的顺序打印出来呢,最后一个图将重新走一遍方法执行过程。
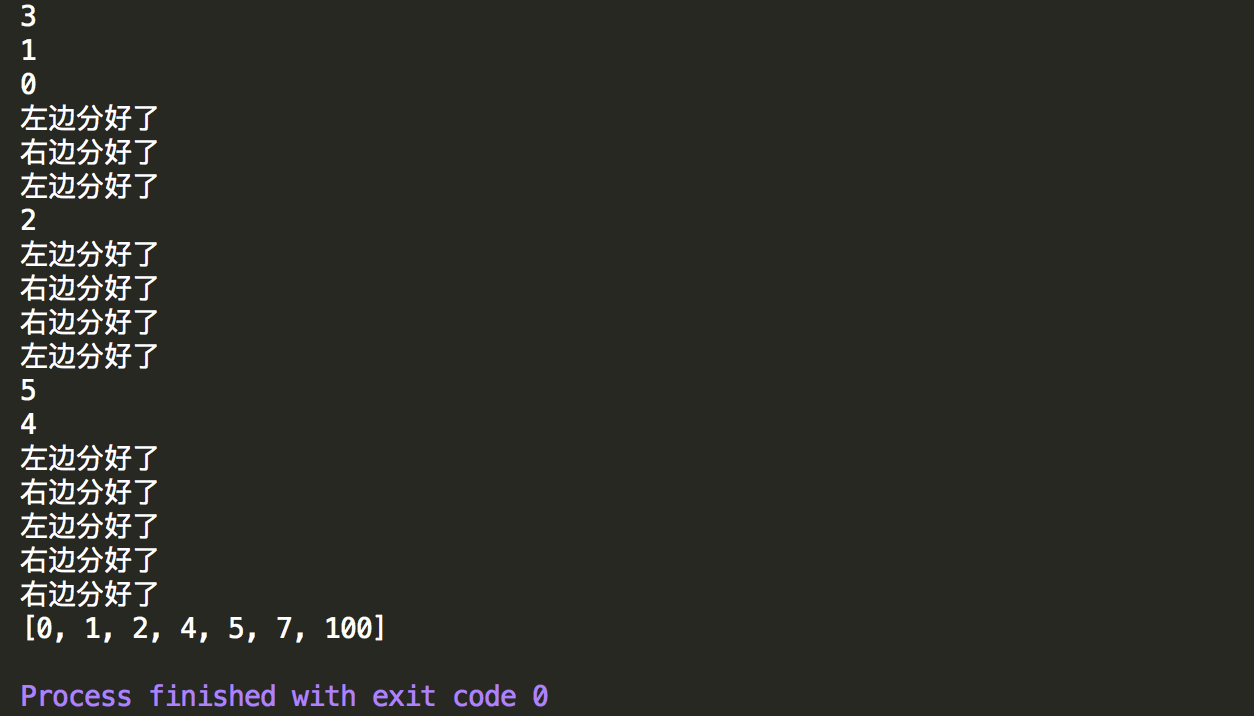
从控制台输出情况可以分析出拆分的过程如下图所示,其中结点中左边数字代表mergesort方法中left参数,右边数字代表right参数,因此根结点的(0,6)代表刚传入的数组下标为起始位置和结束位置。树形结构拆分为左右两部分,代表着方法中首先执行对数组的左拆分,然后对数组的右拆分。然后拆分完的数组,继续执行左拆分和右拆分,如此循环往复直到最后图中left下标和right下标相同,就算完全拆分完成,按照这样的思路去分析一下就可以不难理解控制台输出的内容为啥按照这个顺序来输出了。
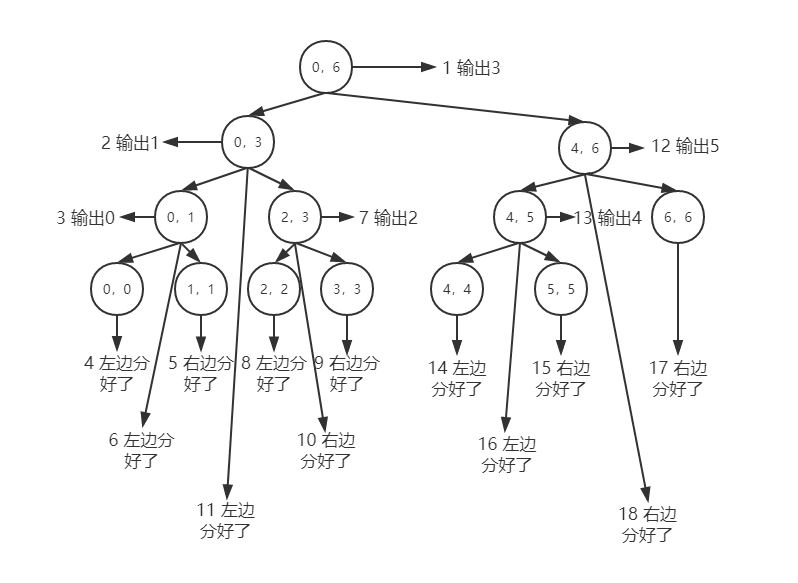
接下来就是并的过程了,既然拆分了必然需要再和起来,那么合又是什么一个过程,根据merge方法写的位置,就是在左右子树都拆分完后执行和并,和并的过程,可能跟画图的顺序不完全一致,即先全部拆分完然后全部一层一层的和并,好像拆分平铺展开然后和并也平铺展开,其实不然,分和并都是有先后顺序的,即整体来看先执行左子树后执行右子树的逻辑。因此根据上图以及merge方法的位置,可以分析出来并的过程大致如下,最后我们可以打桩测试一下验证想法是否正确:
(1)数组中1和5分完后,先合并,变成1,5
(2)然后到了2和7分完后,继续合并,变成2,7
(3)然后往上到(0,3)来看,左右子树执行完了逻辑,最后再需执行并的方法,因此继续合并变成了1,2,5,7
(4)然后往上到(0,6)来看,左子树逻辑执行完后,执行右子树逻辑。所以执行完拆分,得到0和4,接着执行合并方法,变成0,4
(5)然后往上到(4,6)来看,左子树逻辑执行完,右子树本来就不需要拆,因此左右子树都完成了拆,接着执行合并方法,变成0,4,100
(6)到了这一步,以根结点为起点的左右子树都执行完了逻辑,这样接着执行合并,将1,2,5,7和0,4,100再合并,执行合并方法,最后得到排序后的结果
打桩测试结果,在合并完后输出当前数组情况,可以看出跟分析的基本一样。
结论
(1)二叉树是树形结构的一种,其遍历有三种类型,分别为前序遍历,中序遍历和后序遍历
(2)归并排序核心思想是将数组二分后,再逐渐排序后和并成大的数组,其拆分和和并需要用到二叉树遍历思想去理解。
参考博文:
(1)https://www.cnblogs.com/youngchaolin/p/11032616.html#_label4