目录
1 堆的基础概念
2 堆的实现
2.1 实现一个堆类
2.2 将无序数组调整为最大堆
1 堆的基础概念
最大堆:父节点要比每一个子节点的值都要大
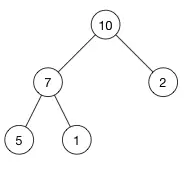
最小堆:父节点要比每一个子节点的值都要小
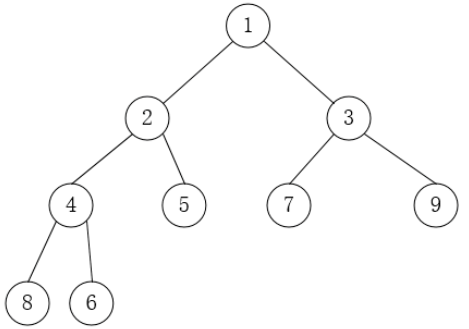
堆可以看做是一个完全二叉树的数组对象
堆的出队入队时间复杂度如下图所示:

2 堆的实现
2.1 实现一个堆类
利用数组实现一个堆的原理:
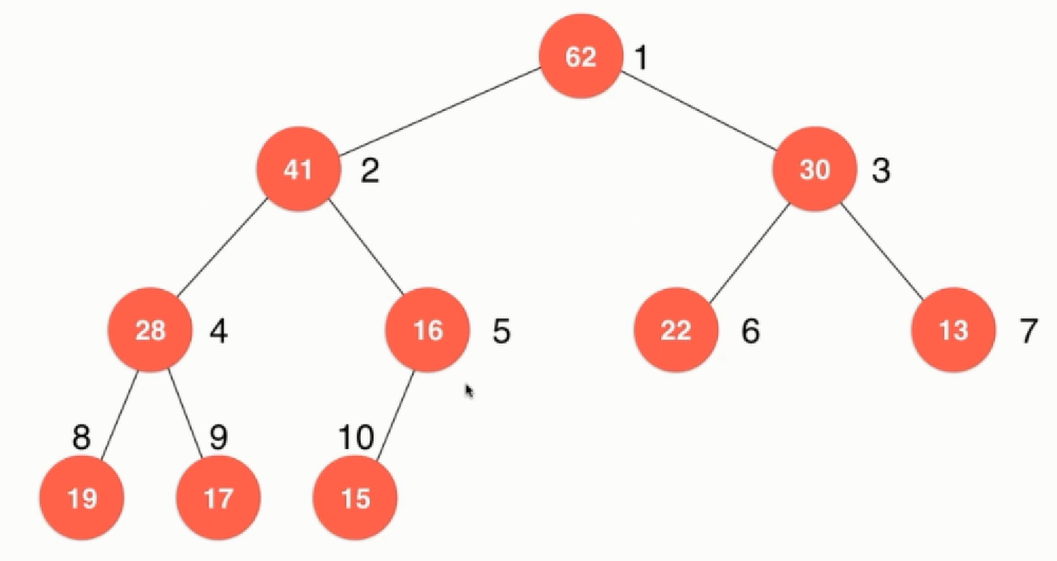
自上而下,自左向右对每一个节点标上序号,可以看出:对于每一个节点而言,每个左节点都是父节点的2倍,右节点是父节点的2倍加1。
堆的经典数组实现如下图所示:

ShiftUp:当需要对堆中添加一个元素时用到了ShiftUp操作。当有一个新元素到来时,按照上面的数组实现,则52在数组末尾,其树形结构如下图所示:
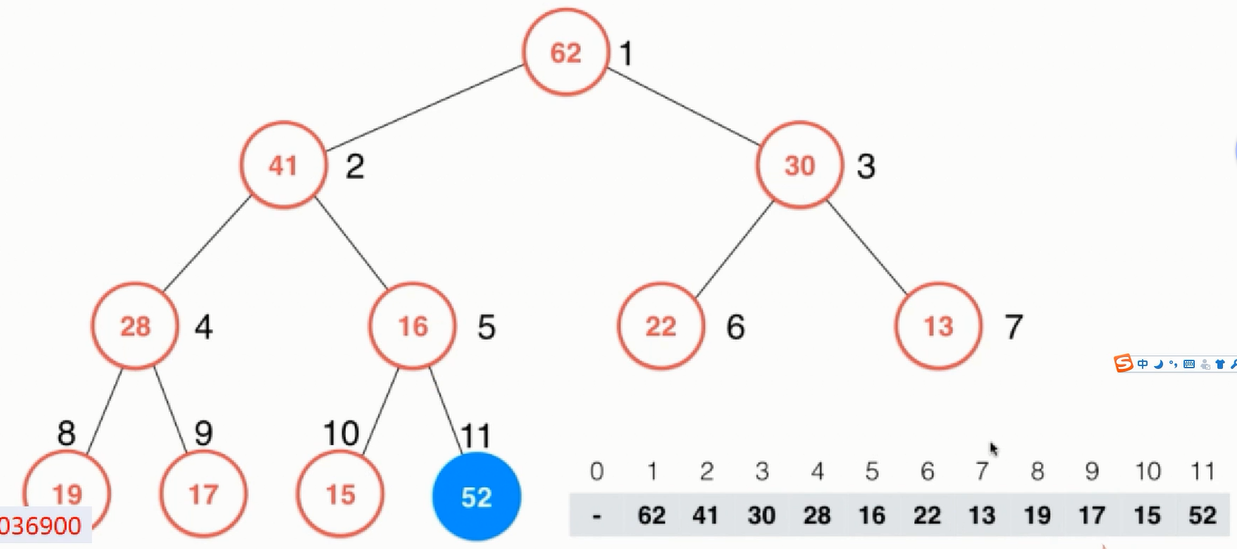
对于上图的树形结构显然是不符合堆的定义的,因此需要对元素进行移动,因为加入了一个元素不满足堆的性质,所以问题就出在新加入元素的部分,比较52的父节点,发现父节点小,交换位置,那么对于52的这个子树就满足了堆的定义了。
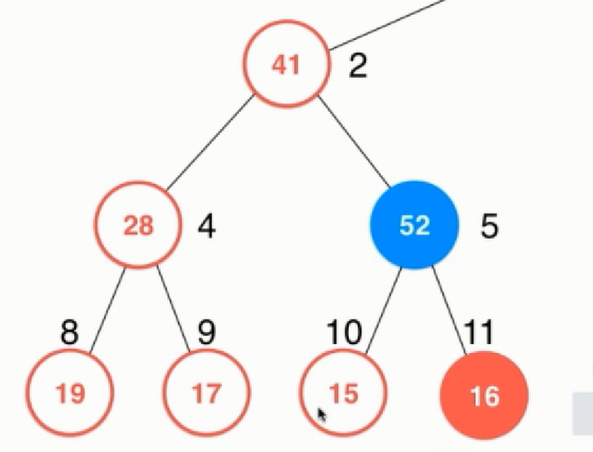
接着继续比较此时52的父节点,发现还是父节点小,因此继续交换:
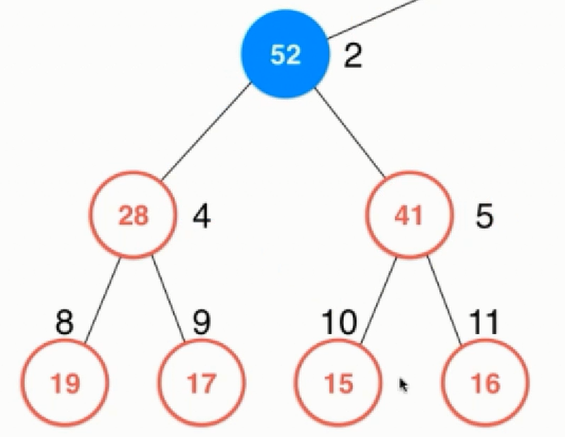
那么最后继续比价52的父节点,发现的确52小,因此不用再交换了,最后如下图所示:
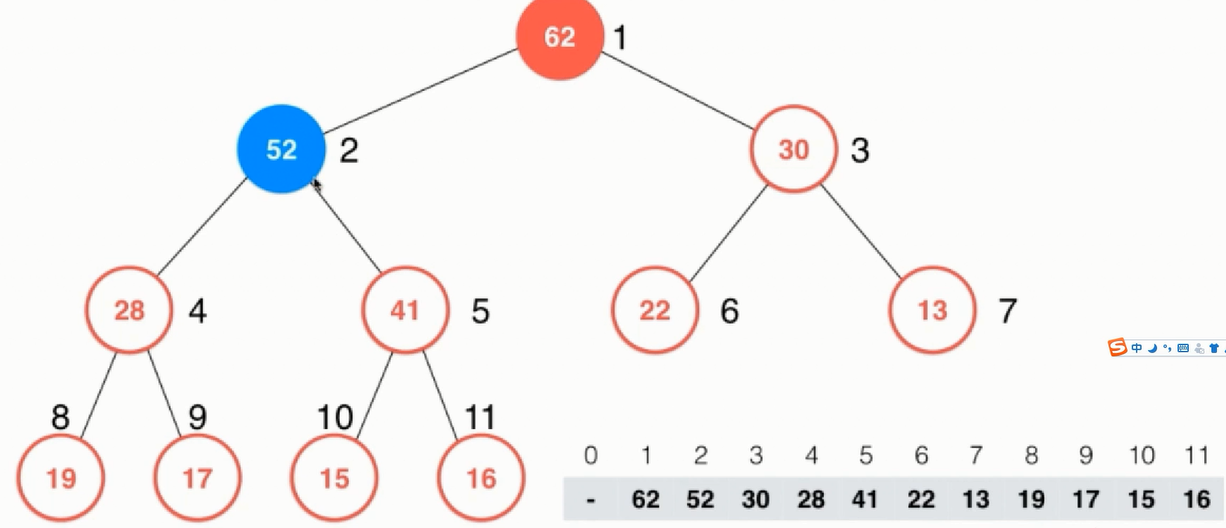
ShiftDown:当从堆中取出一个元素是只能取出堆中跟节点的元素,在下图中即62

取出根节点元素后,把最后一个元素放在根节点,进行下沉操作,因为count表示当前对堆中有多少个元素,当拿出一个元素后把count自减1即可,以count为界限
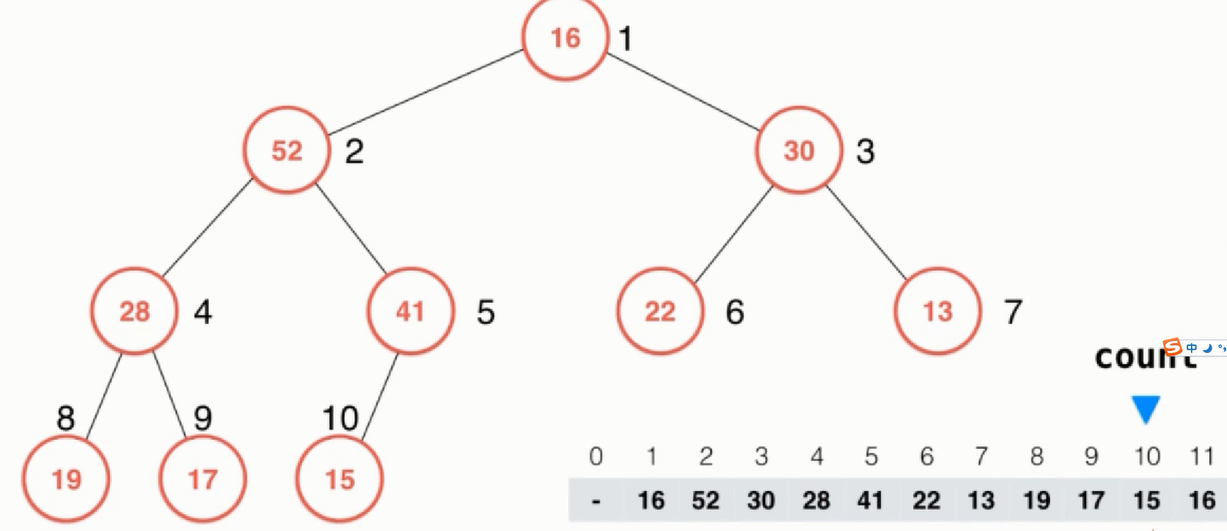
下沉时对两个子节点比较,都比子节点小那么原则就是两个子节点再进行比较谁大就跟谁交换,这里应该和52进行交换:
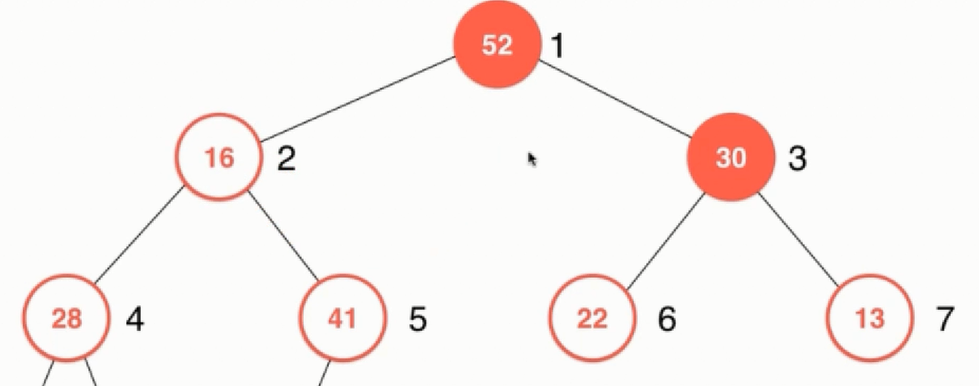
接着继续比较当前16的两个子节点分别是28和41,那么就应该和41进行交换:

接着继续比较,发现15比16小,因此下沉操作到此全部结束,此时堆的结构如下图所示:

最终一个完整的堆操作代码如下图所示:
// 在堆的有关操作中,需要比较堆中元素的大小,所以Item需要extends Comparable,这里的Item就相当于T public class MaxHeap<Item extends Comparable> { // 堆的底层采用数组实现 protected Item[] data; // 实际保存元素的个数 protected int count; // 设定的堆的容量 protected int capacity; // 构造函数, 构造一个空堆, 可容纳capacity个元素 public MaxHeap(int capacity){ data = (Item[])new Comparable[capacity+1]; count = 0; this.capacity = capacity; } // 返回堆中的元素个数 public int size(){ return count; } // 返回一个布尔值, 表示堆中是否为空 public boolean isEmpty(){ return count == 0; } // 向最大堆中插入一个新的元素 item public void insert(Item item){ // 因为有可能再插入一个元素就超出容量,因此在这里断言一下,保证程序安全 assert count + 1 <= capacity; // 注意数组中是从1开始存数据的,因此这里要count+1 data[count+1] = item; count ++; // 插入元素上浮 shiftUp(count); } // 从最大堆中取出堆顶元素, 即堆中所存储的最大数据 public Item extractMax(){ // 进行一个断言即保证堆中是有元素的 assert count > 0; Item ret = data[1]; //取出元素先进行交换堆顶和最后一个元素的操作 swap( 1 , count ); count --; // 进行下沉操作,下沉位置为根节点位置 shiftDown(1); return ret; } // 获取最大堆中的堆顶元素 public Item getMax(){ assert( count > 0 ); return data[1]; } //******************** //* 最大堆核心辅助函数 //******************** private void shiftUp(int k){ // 比较k处的父节点即k/2与k处的大小,要保证k是有意义的,因此要大于1 while( k > 1 && data[k/2].compareTo(data[k]) < 0 ){ //父节点小则交换 swap(k, k/2); k /= 2; } } private void shiftDown(int k){ //当前节点只要有孩子就进行循环操作,在完全二叉树中只要当前节点有左孩子即是有孩子,k*2是其子节点的索引要小于count才代表有左孩子 while( 2*k <= count ){ // 在此轮循环中,data[k]和data[j]交换位置,j表示的左孩子 int j = 2*k; // 判断是否有右孩子,当右孩子大时就让j++此时指向了右孩子 if( j+1 <= count && data[j+1].compareTo(data[j]) > 0 ){ j ++; } // data[j] 是 data[2*k]和data[2*k+1]中的最大值,当前节点如果大于孩子节点就可以停止了 if( data[k].compareTo(data[j]) >= 0 ){ break; } swap(k, j); k = j; } } // 交换堆中索引为i和j的两个元素 private void swap(int i, int j){ Item t = data[i]; data[i] = data[j]; data[j] = t; } }
2.2 将无序数组调整为最大堆
在2.1中是在已经构造好了一个堆进行操作,那么如何从无序数组中构造处一个堆结构?一个随机数组如下图所示:
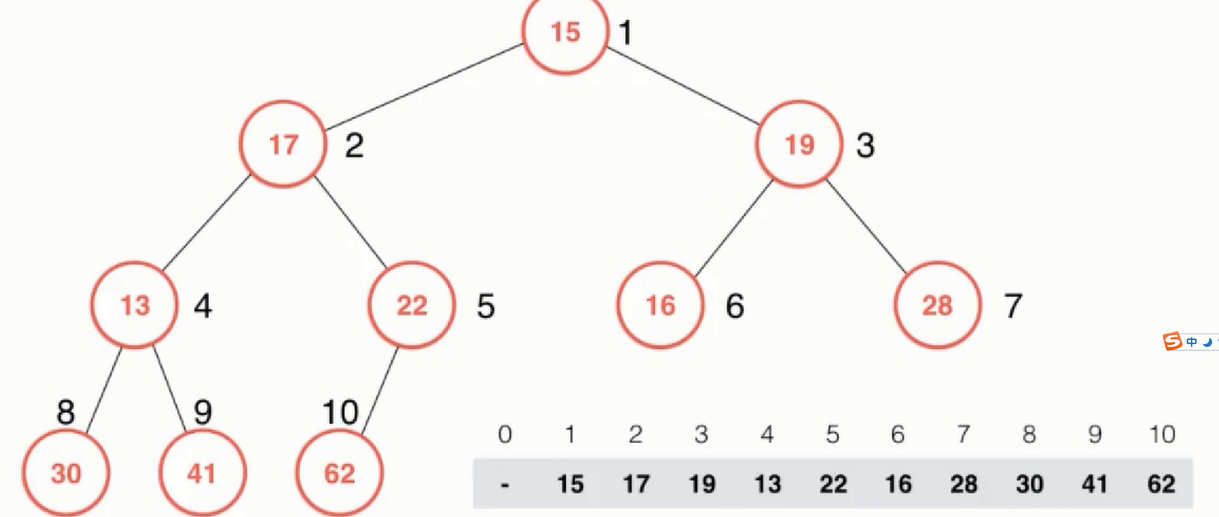
Heapify操作:利用数组构建出堆结构
首次开始时从最底层的节点,可以认为叶子节点便是一个已经最大堆,只不过这个最大堆的元素只有一个。有一个完全二叉树的性质:第一个非叶子节点的索引是完全二叉树的个数除以2,在上面的二叉树中便是10/2 = 5。注意这里的第一个非叶子节点是从右向左、从底向下而来的。在第一个非叶子节点上执行下沉操作,其结果如下图所示:
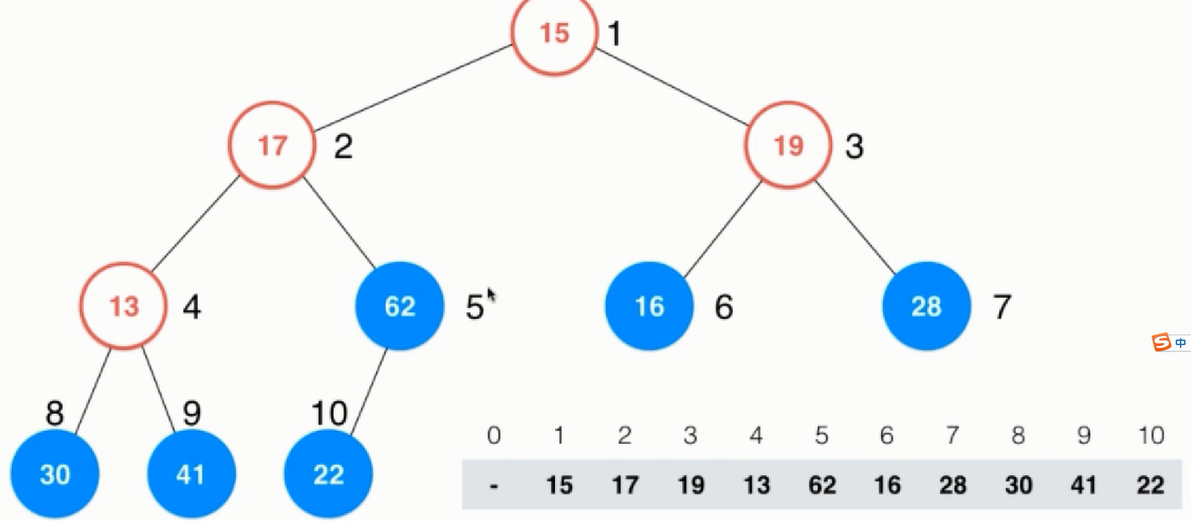
依照这样的格式分别考虑前面的非叶子节点4、3进行下沉操作,最后结果如下图所示:
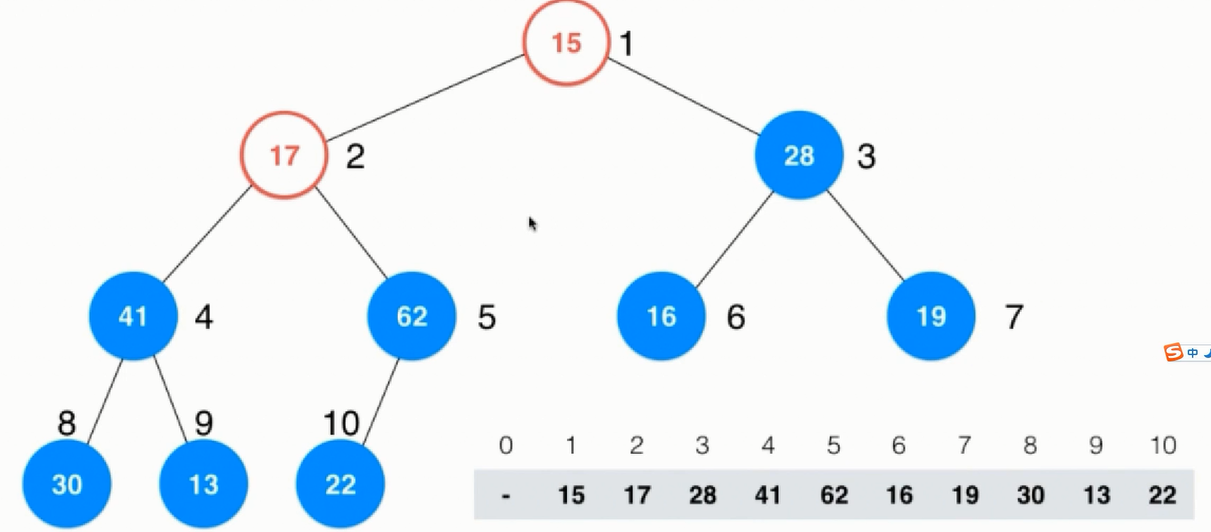
接着是元素17,首先和62交换位置,然后因为22大所以还要交换位置,最后结果如下图所示:
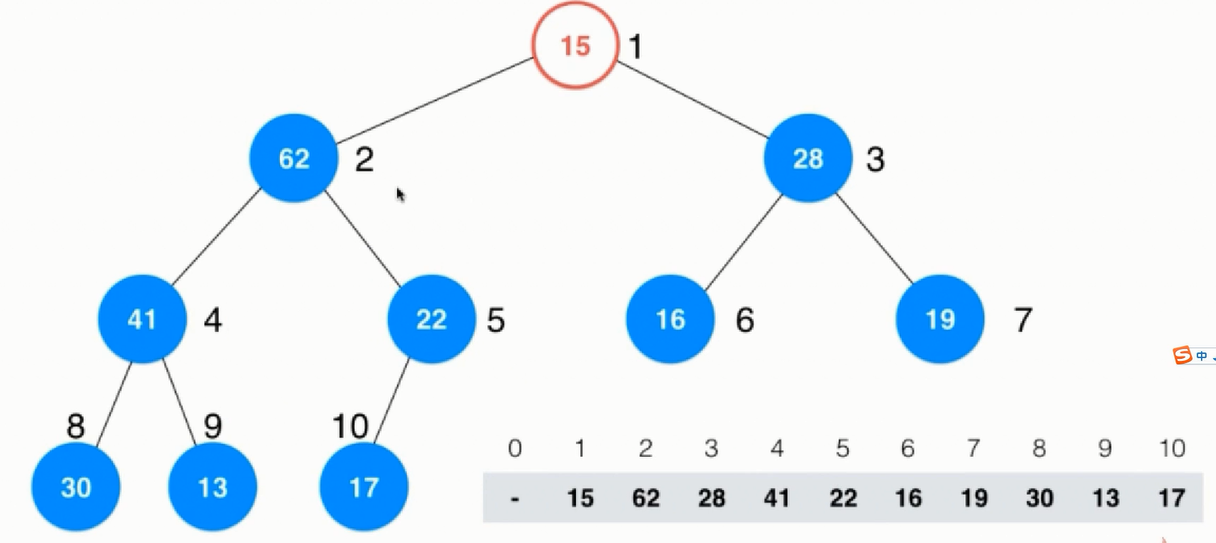
继续考虑前面的节点,最后实现的树如下图所示:

// 构造函数, 通过一个给定数组创建一个最大堆,该构造堆的过程, 时间复杂度为O(n) public MaxHeap(Item arr[]){ int n = arr.length; data = (Item[])new Comparable[n+1]; capacity = n; // 将数组中的元素存储到类中定义的数组 for( int i = 0 ; i < n ; i ++ ){ data[i+1] = arr[i]; } count = n; // 按照上面的思路进行下沉 for( int i = count/2 ; i >= 1 ; i -- ){ shiftDown(i); } }
注:关于算法复杂度分析:将n个元素逐个插入到一个空堆中(下沉上浮操作)算法复杂度是O(nlogn);heapify过程的算法复杂度为O(n)
0