目录
0 二分搜索
1 二分搜索树
2 插入元素
3 查找元素
4 二分搜索树的遍历---深度优先
5 二分搜索树的层序遍历---广度优先
6 二分搜索树删除一个节点
1 二分搜索
这部分代码已经在数组中给出了详细的介绍,此处只给出实现代码:
//在一个有效整数数组中根据二分法查找一个整数 public int binarySearch(int[] arr,int target){ //在[left...r]的区间范围内寻找target int left = 0,r = arr.length-1; //当left==r时,区间仍然是有效的只不过此时区间中只有一个元素 while (left <= r){ //防止溢出的求中值 int mid = left+(r-left)/2; if (arr[mid] == target){ return mid; } if (target > arr[mid]){ //target在[mid+1...r]中 left = mid + 1; }else{ //target在[left...mid-1]中 r = mid - 1; } } //当搜索不到时就返回-1 return -1; }
在此处给出二分查找的递归版本,递归版本要比循环的性能上要稍微差一点,但整体上还是一个级别的时间复杂度的,都是O(logn)级别:
// 二分查找法的递归版本 public static int find(Comparable[] arr, Comparable target) { return find(arr, 0, arr.length-1, target); } private static int find(Comparable[] arr, int left, int r, Comparable target){ if (left > r){ //当查不到元素时就返回-1 return -1; } int mid = left + (r-left)/2; if (arr[mid].compareTo(target) == 0){ return mid; }else if (arr[mid].compareTo(target) > 0){ return find(arr,left,mid - 1,target); }else { return find(arr,mid+1,r,target); } }
注:上面的查找都是考虑到数组中没有重复元素的情况,如果有重复元素那么返回的数值索引可能会不一样,因此有另外两个函数floor和ceil分别查找第一次出现的索引和最后一次出现的索引。
2 树的基本概念
(1)二叉树
每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点),并且,二叉树的子树有左右之分,其次序不能任意颠倒。
(2)二叉树的性质
(1)若二叉树的层次从0开始,则在二叉树的第i层至多有2^i个结点(i>=0)。
(2)高度为k的二叉树最多有2^(k+1) - 1个结点(k>=-1)。 (空树的高度为-1)
(3)对任何一棵二叉树,如果其叶子结点(度为0)数为m, 度为2的结点数为n, 则m = n + 1。
(3)完美二叉树(满二叉树)
一个深度为k(>=-1)且有2^(k+1) - 1个结点的二叉树称为完美二叉树。
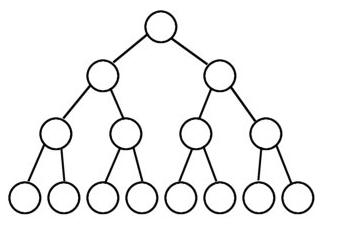
(4)完全二叉树
完全二叉树从根结点到倒数第二层满足完美二叉树,最后一层可以不完全填充,其叶子结点都靠左对齐。

3 二分搜索树
二分搜索树一般查用于查找表的实现,即字典数据结构:

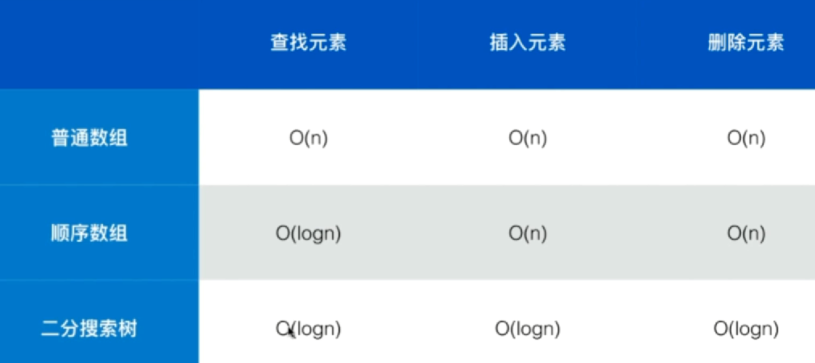
优势:不仅可查找数据;还可以高效地插入,删除数据,还可以方便维护数据之间的关系。那么对于查找表这种数据结构,其底层采用不同的实现形式,所带来的性能也是不同的,具体性能如下图所示:
二分搜索树的定义:是一个二叉树,每个节点的键值大于左孩子,小于右孩子。二分搜索树与堆不同,不一定是完全二叉树,因此底层不容易直接用数组表示故采用链表来实现二分搜索树。对于具体二分搜索树可以看如下图所示:
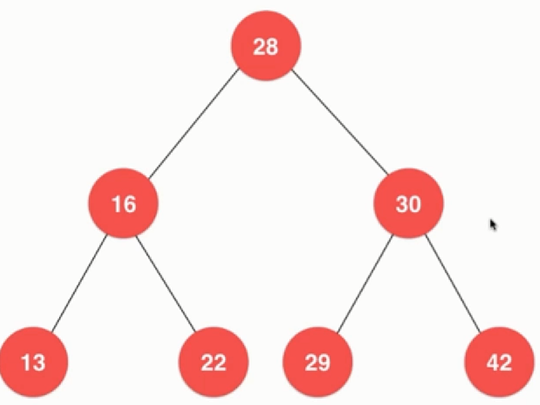
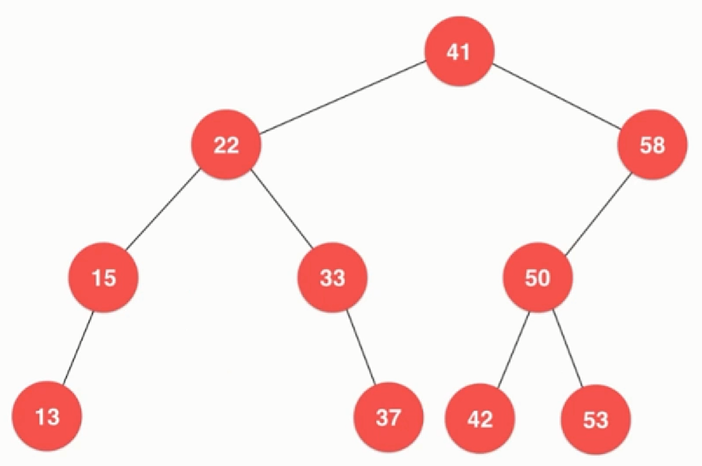
对于实际问题中,需要存储的还有value值,但是在分析中一般更重要的是分析key值,在上图中也是只存储了key值并不体现value值。在二分搜索树中对于前中后序其本质在于位置的不同,与遍历的次数是没有关系的,在一次遍历中也可以有多种遍历方式。
2 插入元素
如下图中,想要把元素60插入树中,首先要比较的就是根节点,发现元素比根节点大则应插入在根节点的右侧
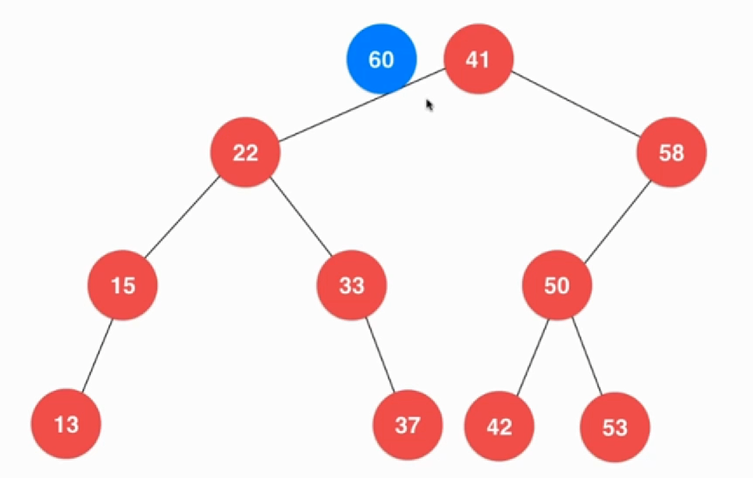
继续比较发现58比60小那么应该在58的右侧,因为58右侧无节点便可以直接插入了。
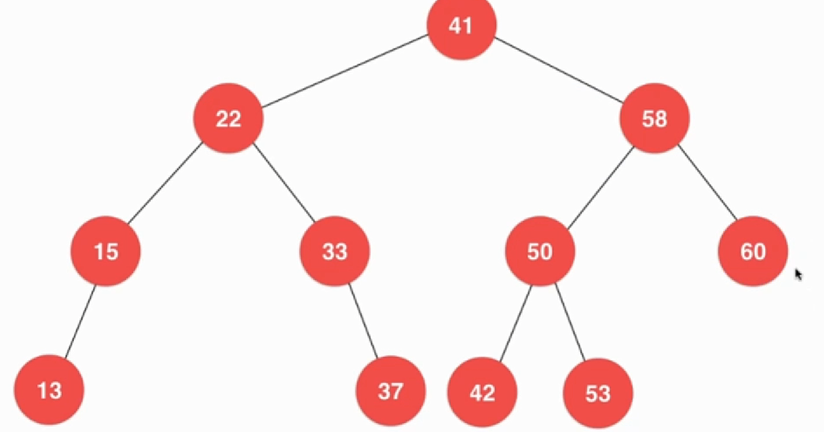
当插入元素小时如下图,当插入28时,因为28小,所以应该在41的左节点侧
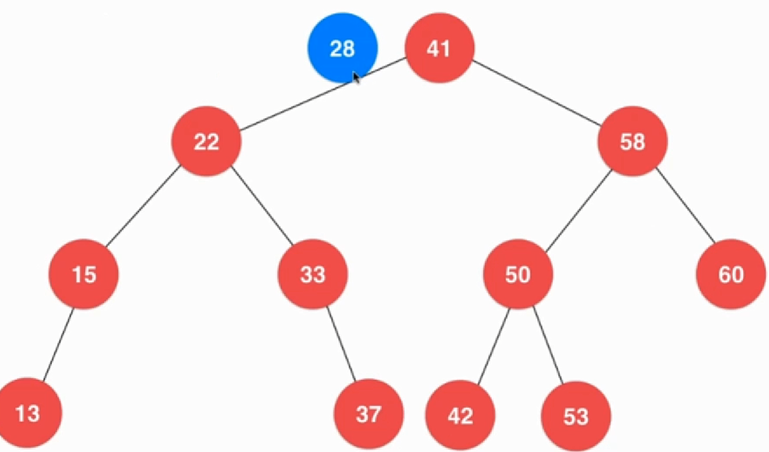
因为28又比22大因此会在22右子树中,继续比较28与33,因为28小所以应该在33的左子树中
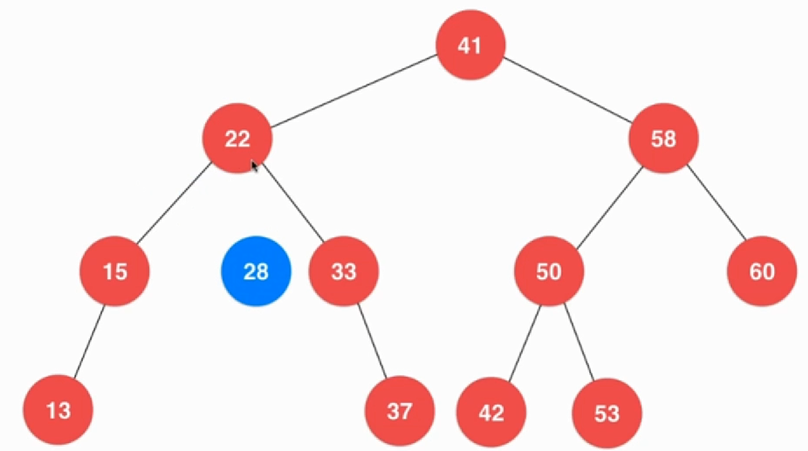
33无子节点了,因此便可以插入了28,最终插入效果如下:

在插入节点时还有一种特殊情况即插入的元素和树中的值相等,此时应该用插入的元素直接覆盖掉旧元素即可:

代码如下:
// 二分搜索树 // 由于Key需要能够进行比较,所以需要extends Comparable<Key> public class BST<Key extends Comparable<Key>, Value> { // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现 private class Node { private Key key; private Value value; private Node left, right; public Node(Key key, Value value) { this.key = key; this.value = value; left = right = null; } } private Node root; // 根节点 private int count; // 树种的节点个数 // 构造函数, 默认构造一棵空二分搜索树 public BST() { root = null; count = 0; } // 返回二分搜索树的节点个数 public int size() { return count; } // 返回二分搜索树是否为空 public boolean isEmpty() { return count == 0; } // 向二分搜索树中插入一个新的(key, value)数据对 public void insert(Key key, Value value){ root = insert(root, key, value); } // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法 // 返回插入新节点后的二分搜索树的根 private Node insert(Node node, Key key, Value value){ if( node == null ){ count ++; return new Node(key, value); } //如果相等便更新数据 if( key.compareTo(node.key) == 0 ){ node.value = value; } else if( key.compareTo(node.key) < 0 ){ node.left = insert( node.left , key, value); } else { // key > node->key node.right = insert( node.right, key, value); } return node; } }
3 查找元素
对于二分搜索树的查找元素其实和插入部分元素相同的,其思路是基本一致的,在这里直接给出代码:
// 查看二分搜索树中是否存在键key public boolean contain(Key key){ return contain(root, key); } // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null public Value search(Key key){ return search( root , key ); } // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法 private boolean contain(Node node, Key key){ //如果最终查不到返回false if( node == null ) { return false; } // 查找到了 if( key.compareTo(node.key) == 0 ){ return true; } else if( key.compareTo(node.key) < 0 ){ // 当前key小于节点便在左侧查找 return contain( node.left , key ); } else{// key > node->key // 当前key小于节点便在右侧查找 return contain( node.right , key ); } } // 在以node为根的二分搜索树中查找key所对应的value, 递归算法 // 若value不存在, 则返回NULL private Value search(Node node, Key key){ if( node == null ){ return null; } if( key.compareTo(node.key) == 0 ){ return node.value; } else if( key.compareTo(node.key) < 0 ){ return search( node.left , key ); } else {// key > node->key return search( node.right, key ); } }
4 二分搜索树的遍历---深度优先
对树中一个节点的遍历其图示如下(前序遍历),可以看出相当于父节点其实是访问了三次的,第一次来到父节点,然后访问左子树,再回到父节点,访问右子树,再回到父节点。

对于前中后序遍历其代码如下:
// 二分搜索树的前序遍历 public void preOrder(){ preOrder(root); } // 二分搜索树的中序遍历 public void inOrder(){ inOrder(root); } // 二分搜索树的后序遍历 public void postOrder(){ postOrder(root); } // 对以node为根的二叉搜索树进行前序遍历, 递归算法 private void preOrder(Node node){ if( node != null ){ // 输出遍历的节点值 System.out.println(node.key); preOrder(node.left); preOrder(node.right); } } // 对以node为根的二叉搜索树进行中序遍历, 递归算法 private void inOrder(Node node){ if( node != null ){ inOrder(node.left); System.out.println(node.key); inOrder(node.right); } } // 对以node为根的二叉搜索树进行后序遍历, 递归算法 private void postOrder(Node node){ if( node != null ){ postOrder(node.left); postOrder(node.right); System.out.println(node.key); } }
从上面的代码中也可以看出,三种遍历方式其本质都是一样的,只不过在遍历时其输出的语句的值的位置不同而已。
5 二分搜索树的层序遍历---广度优先
层序遍历需要借助另一种数据结构即:队列
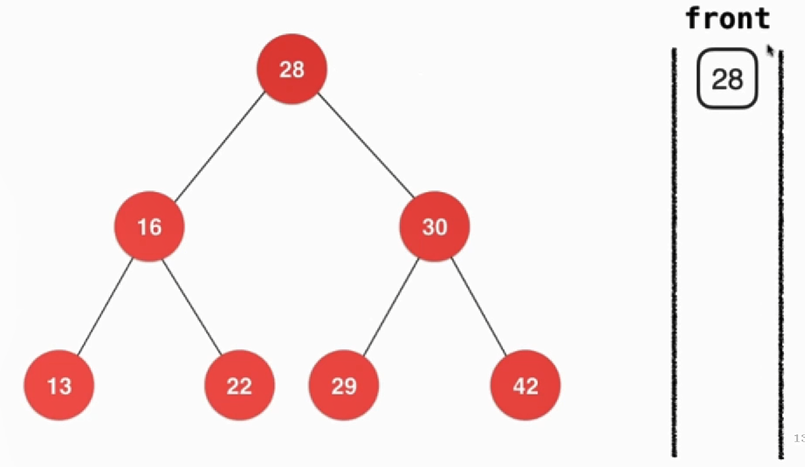

在树中遍历到节点时便把元素入队如28,当队列中元素不为空时便弹出对首元素,在弹出后把该节点的左右子节点入队。
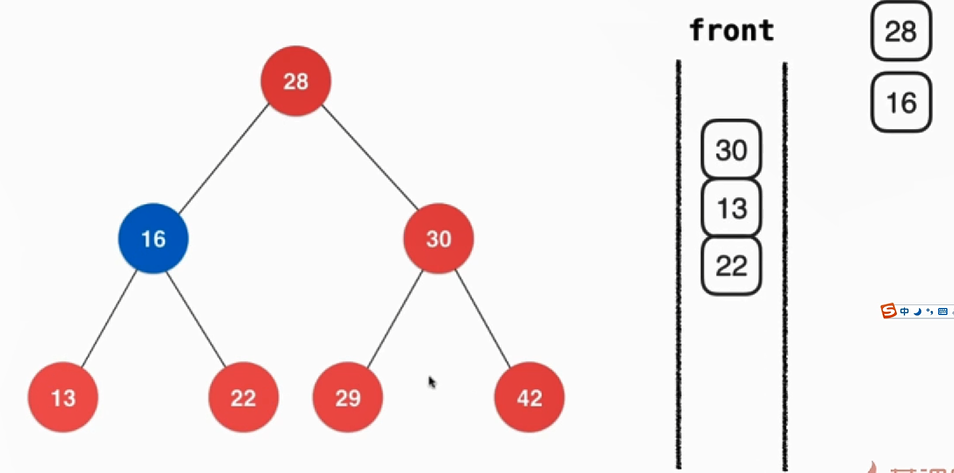
继续弹出队首元素16,然后再把16的左右子节点入队,此时整个队列如上图所示。接着把30出队,再把30的左右子节点入队,依次进行下去即可。在遍历到13这些叶子节点时其实还是重复的上面的操作,只不过是叶子节点没有子节点了,所以不会有新元素入队。其层序遍历如下图所示:
// 二分搜索树的层序遍历 public void levelOrder(){ // 队列的底层采用链表实现 Queue<Node> q = new LinkedList<Node>(); q.add(root); while( !q.isEmpty() ){ // 当队列不为空时首先队首元素出队 Node node = q.remove(); // 输出节点值 System.out.println(node.key); // 左右子节点入队 if( node.left != null ){ q.add( node.left ); } if( node.right != null ){ q.add( node.right ); } } }
层序遍历有一个非常好的优点便是其时间复杂度为O(n)。
6 二分搜索树删除一个节点
找到一个节点,然后删除这是简单的,问题的关键在于当删除了节点后如何还能保持二分搜索树的性质。直接讨论删除比较困难,先从最简单的入手如:删除二分搜索树中的最大值和最小值节点。因为二分搜索树的性质为每个节点值大于左孩子小于右孩子,因此不断地进行左侧递归遍历,直至再无左子树便是整个二分搜索树中最小值;对于最大值也是类似,便是不断进行右侧递归遍历。对于如下图所示的二分搜索树很简单,只需要直接删除最小元素即可了。

当但一个二分搜索树为下图情况时,便不是直接删除节点22了,删除之后如何处理剩下的元素。

根据二分搜索树的性质,虽然22的右子树节点一定比22大,但也一定比22的父亲节点要小,因此可以直接把右子树直接向上移动即可。

同样的删除最大值也是类似的思路,如下图中删除最大值,则需要把左子树节向上移动填充即可。
代码如下:
// 返回以node为根的二分搜索树的最小键值所在的节点 private Node minimum(Node node){ if( node.left == null ){ return node; } // 不断进行左侧递归遍历 return minimum(node.left); } // 返回以node为根的二分搜索树的最大键值所在的节点 private Node maximum(Node node){ if( node.right == null ){ return node; } // 不断进行右侧递归遍历 return maximum(node.right); } // 删除掉以node为根的二分搜索树中的最小节点,返回删除节点后新的二分搜索树的根 private Node removeMin(Node node){ // 当再无左节点时便可以删除了 if( node.left == null ){ // 返回的是当前节点的右节点 Node rightNode = node.right; // 让当前节点的右节点为空,相当于释放了内存,便于回收 node.right = null; count --; return rightNode; } node.left = removeMin(node.left); return node; } // 删除掉以node为根的二分搜索树中的最大节点,返回删除节点后新的二分搜索树的根 private Node removeMax(Node node){ if( node.right == null ){ Node leftNode = node.left; node.left = null; count --; return leftNode; } node.right = removeMax(node.right); return node; }
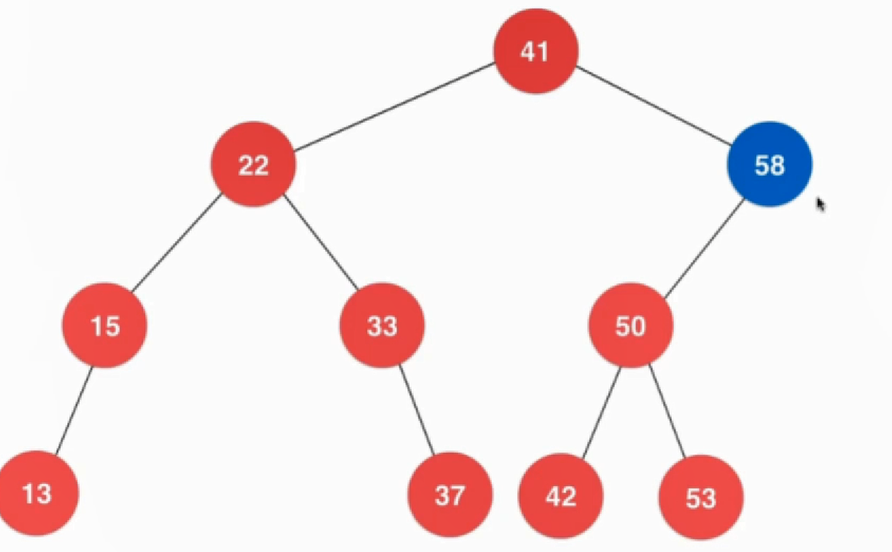
从上面的删除最大最小值可以看出,最大值只有左节点,最小值只有右节点。因此可以进行推广删除一个只有左节点或者只有右节点的节点。那么如何删除一个有左右子节点的节点,其图示如下:

待删除的节点是58,那么应该找一个节点去填充位置,因为二分搜索树的性质右子树的节点都大于左子树的节点,父节点要大于左子树小于右子树,所以填充的节点应该是右子树中的最小值,即59。 删除部分代码如下:
// 二分搜索树 // 由于Key需要能够进行比较,所以需要extends Comparable<Key> public class BST<Key extends Comparable<Key>, Value> { // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现 private class Node { private Key key; private Value value; private Node left, right; public Node(Key key, Value value) { this.key = key; this.value = value; left = right = null; } // 进行节点的赋值,为了解决successor中指向为空的问题 public Node(Node node){ this.key = node.key; this.value = node.value; this.left = node.left; this.right = node.right; } } private Node root; // 根节点 private int count; // 树种的节点个数 // 构造函数, 默认构造一棵空二分搜索树 public BST() { root = null; count = 0; } // 删除掉以node为根的二分搜索树中键值为key的节点, 递归算法,返回删除节点后新的二分搜索树的根 Node remove(Node node, Key key){ if( node == null ){ return null; } if( key.compareTo(node.key) < 0 ){ node.left = remove( node.left , key ); return node; } else if( key.compareTo(node.key) > 0 ){ node.right = remove( node.right, key ); return node; } else{ // 前面的两个判断其实就是一个寻找的过程 // 待删除节点左子树为空的情况,与删除最小值相同 // 当该节点左右孩子都为空时其实是进入了这个if中 if( node.left == null ){ Node rightNode = node.right; node.right = null; count --; return rightNode; } // 待删除节点右子树为空的情况,与删除最大值相同 if( node.right == null ){ Node leftNode = node.left; node.left = null; count--; return leftNode; } // 待删除节点左右子树均不为空的情况 // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点,用这个节点顶替待删除节点的位置 Node successor = new Node(minimum(node.right)); // 多了一个新节点所以count要自增 count ++; // 删除节点右子树中的最小值。在此处要注意上面是把待删除节点右子树的最小值赋值给sccessor,当删除最小值后suceessor也就指向空了 // 因此要用new 而不是直接赋值 successor.right = removeMin(node.right); successor.left = node.left; // 让node的左右节点都为空 node.left = node.right = null; // 此时node已经被删除了,因此count要自减 count --; return successor; } } }
注:要注意当数据是递增的时候二分搜索树就会退化成一个链表,此时时间复杂度会很高,因此才有了后面的红黑树、平衡二叉树等
0