C. Permutation Cycle
For a permutation P[1... N] of integers from 1 to N, function f is defined as follows:
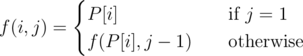
Let g(i) be the minimum positive integer j such that f(i, j) = i. We can show such j always exists.
For given N, A, B, find a permutation P of integers from 1 to N such that for 1 ≤ i ≤ N, g(i) equals either A or B.
The only line contains three integers N, A, B (1 ≤ N ≤ 106, 1 ≤ A, B ≤ N).
If no such permutation exists, output -1. Otherwise, output a permutation of integers from 1 to N.
9 2 5
6 5 8 3 4 1 9 2 7
3 2 1
1 2 3
In the first example, g(1) = g(6) = g(7) = g(9) = 2 and g(2) = g(3) = g(4) = g(5) = g(8) = 5
In the second example, g(1) = g(2) = g(3) = 1
(一)何谓Permutation Cycle
以例1中的6 5 8 3 4 1 9 2 7
第一个数是6,以6为位置,则第六个数是1,以1为位置,第一个数是6,以6为位置,第六个数是1……,这样6和1就构成了一个圈子。f(1) = 6, f(6) = 1,最短的周期是2
第二个数是5,以5为位置,第五个数是4,以4为位置,第四个数是3,以3为位置,第三个数是8,以8为位置,第八个数是2,以2为位置,第2个数是5,以5为位置,第五个数是4……这样5,4,3,8,2也构成了一个圈子。f(5) = 4, f(4) = 3, f(3) = 8, f(8) = 2, f(2) = 5,最短的周期是5。
(二)例子分析
对于例1中的6 5 8 3 4 1 9 2 7
p[1] = 6, p[2] = 5, p[3] = 8, p[4] = 3, p[5] = 4, p[6] = 1, p[7] = 9, p[8] = 2, p[9] = 7
f(1, j) = f(6, j-1) = p[6] = 1,此时j - 1 = 1 ==> j = 2 ==> g(1) = 2
f(2, j) = f(5, j-1) = f(4, j-2) = f(3, j-3) = f(8, j-4) = p[8] = 2,此时j - 4 = 1 ==> j = 5 ==> g(2) = 5
f(3, j) = f(8, j-1) = f(2, j-2) = f(5, j-3) = f(4, j-4) = p[4] = 3,此时j - 4 = 1 ==> j = 5 ==> g(3) = 5
……
所以,g(1) = g(6) = g(7) = g(9) =2, g(2) = g(3) = g(4) = g(5) = g(8) = 5
对于例2中的1,2,3
p[1] = 1, p[2] = 2, p[3] = 3
f(1, j) = p[1] = 1 ==> j = 1 ==> g(1) = 1
f(2, j) = p[2] = 2 ==> j = 1 ==> g(2) = 1
f(3, j) = p[3] = 3 ==> j = 1 ==> g(3) = 1
所以,g(1) = g(2) = g(3) = 1
(三)思路
对于本题来说,实际上就是求 Ax + By = N,x >= 0, y >= 0
对于例1,A = 2, B = 5, N = 9,Ax + By = N ==> 2x + 5y = 9 ==> x = 2, y = 1
也就是说,9个数里,有两组2个数,使得g(i) = 2。这两组数分别为2, 1和4, 3
有一组5个数,使得g(i) = 5,这组数为6,7,8,9,5
再举一例,A = 3, B = 6, N = 9
3x + 6y = 9 ==> x = 1, y = 1
也就是说,9个数里,有一组3个数,使得g(i) = 3。这组数为2,3,1
另有一组6个数,使得g(i) = 6。这组数为5,6,7,8,9,4
再举一例,A = 4, B = 6, N = 9
4x + 6y = 9,无解
题目思路来源:
链接:https://www.jianshu.com/p/c14d90b9db75

#include<cstdio> int main() { int n, a, b; int cnta, cntb; int flag = false; scanf("%d %d %d", &n, &a, &b); for (int i = 0; i * a <= n; i++) { int t = n - a * i; if (t % b == 0) { cnta = i; cntb = t / b; flag = true; break; } } int num = 1; int lastNum = num; if(!flag) { printf("-1 "); } else { for(int i = 1;i <= cnta;i++) { for(int k = 1;k < a;k++) { printf("%d ",++num); } printf("%d ",lastNum); num++; lastNum = num; } for(int i = 1;i <= cntb;i++) { for(int k = 1;k < b;k++) { printf("%d ",++num); } printf("%d ",lastNum); num++; lastNum = num; } } return 0; }
