用Dancing Links解决数独(Sudoku)问题

Dancing Links

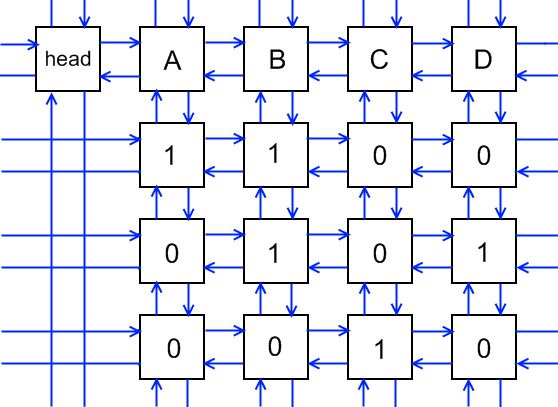
Dancing Links可以认为是一种数据结构（好像本校面向大二年级开设的数据结构课程中就有它），其实就是一种链表，准确地讲是十字双向循环链表。

十字：普通链表是一条线，而十字链表就是一张网，每个结点不仅有左右邻居，还有上下邻居。
双向：双向是链表中很经典的概念，即每个结点要保存上下左右四个方向的邻居指针。
循环：循环也是比较常见的概念了，即每一行的最左结点的左邻居设置为这一行的最右结点，最右结点的右邻居设置为最左结点；每一列同理。

至此，Dancing Links的基本样子就有了。对于有一点点数据结构基础的同学来说（比如我），十字双向循环链表可能比一整页的详细描述更好懂吧……
不难看出，这个数据结构很像是矩阵，很适合用来维护稀疏矩阵的元素。
不过，Dancing Links一般还含有两种特殊类型的结点——头结点（Head）和列结点（Column）。
如果我们把矩阵元素坐标用((1...n,1...m))来表示，那么头结点就是((0,0))，列结点就是((0,1...m))。
头结点可以看为是我们访问所有结点的一个入口，额外创建一个这样的头结点是因为我们在后续过程中始终不会将该结点移除，不像其他结点可能被删掉（那样我们用那个结点就不一定能找到当前剩余的全部元素了）。
列结点私以为是用来辅助Dancing Links X算法的（一个用来解决Exact Cover问题的算法）。

Dancing Links X 算法

Exact Cover 问题

设全集是(S)，给出一些子集(S_i)，要求选一些子集出来，恰好包含(S)的所有元素且每个元素只被一个子集包含。

算法描述

首先用01矩阵(A)描述上面的问题。
每一行代表一个子集，每一列代表一个元素。
比如子集(S_i)包含元素(a_j)，那么(A_{i,j}=1)；如果子集(S_i)不包含元素(a_j)，那么(A_{i,j}=0)。
问题转化为选择一些行，这些行上的1恰好不重复地覆盖每一列。
采用递归搜索的方法解决此问题。

1. 选择矩阵中一列(c)，考虑用某该列为1的行来覆盖这一列。
2. 枚举该列为1的行，比如(r)行。
3. 删除因为此次决策被覆盖掉的列、行，以及因为此次决策而不可能选取的行。
4. 递归搜索，从第1条开始。
5. 回溯，恢复本次决策删掉的所有行和列。

算法描述大概就是这样子的。

Arxiv Paper

数独问题

要用Dancing Links X来解决数独问题，首先需要将其转化为Exact Cover问题，在此我们以9x9的数独为例。

我们将数独的规则翻译为以下四条——

1. 每个格子必须且仅能填1～9中的一个数。
2. 每一行上1～9每个数必须且仅用一次。
3. 每一列上1～9每个数必须且仅用一次。
4. 每个子宫格内1～9每个数必须且仅用一次。

我们现在有若干选择，每个选择表示为((x,y,k))，意思是在((x,y))这个格子内填(k)。
我们给每个选择一个唯一的标号，不妨令((x,y,k))的标号就是(81 imes (x-1) + 9 imes (y-1) + k)。
我们将每个选择对应到Exact Cover问题中的一个子集上，也就是Dancing Links矩阵的一行上，然后通过在每行的特定位置放一些1来翻译上面的4个条件。
对于第一条，要限制((x,y))这个格子填一个数，我们用矩阵的一列，这一列上所有代表本格子的选择（矩阵中的行）值为1。
对于第二条，要限制某一行(r)上填1～9，我们用矩阵的一列，这一列上每个在本行的选择（矩阵中的行）值为1。
对于第三条，……
对于第四条，……
问题转化完成之后，直接用DLX来解决即可。
9x9的数独问题
16x16的数独问题

class Base(object):
    def __init__(self, id):
        self.id = id
        self.l = self
        self.r = self
        self.u = self
        self.d = self

class Head(Base):
    def __init__(self):
        super().__init__(id=('head'))

class Cell(Base):
    def __init__(self, x, y, c=None):
        super().__init__(id=('cell', x, y))
        if c:
            self.c = c
            self.u = c.u
            self.d = c
            self.u.d = self
            self.d.u = self
            self.c.s += 1

class Coln(Base):
    def __init__(self, c):
        super().__init__(id=('coln', c))
        self.s = 0

class DancingLinks(object):
    def __init__(self, head):
        self.h = head

    def _cover(self, c):
        c.r.l = c.l
        c.l.r = c.r
        i = c.d
        while i != c:
            j = i.r
            while j != i:
                j.d.u = j.u
                j.u.d = j.d
                j.c.s -= 1
                j = j.r
            i = i.d

    def _uncover(self, c):
        i = c.u
        while i != c:
            j = i.l
            while j != i:
                j.c.s += 1
                j.u.d = j
                j.d.u = j
                j = j.l
            i = i.u
        c.l.r = c
        c.r.l = c

    def _choose_col(self):
        c, s = None, float('inf')
        i = self.h.r
        while i != self.h:
            if s > i.s:
                c, s = i, i.s
            i = i.r
        return c

    def _search(self, s):
        if self.fall or len(self.ans) == 0:
            if self.h == self.h.r:
                self.ans.append(s[:])
            else:
                c = self._choose_col()
                self._cover(c)
                i = c.d
                while i != c:
                    s.append(i.id)
                    j = i.r
                    while j != i:
                        self._cover(j.c)
                        j = j.r
                    self._search(s)
                    j = i.l
                    while j != i:
                        self._uncover(j.c)
                        j = j.l
                    i = i.d
                self._uncover(c)

    def run(self, find_all=False):
        self.ans = []
        self.fall = find_all
        if self.h != self.h.r:
            self._search([])
        return self.ans

    @classmethod
    def from_sudoku(cls, grid):
        n = len(grid)
        m = int(n**0.5)
        h = Head()
        a = []
        for i in range(4*n*n):
            c = Coln(i)
            c.r = h
            c.l = h.l
            c.l.r = c
            c.r.l = c
            a.append(c)
        pos = lambda x, y, k: x * n + y
        row = lambda x, y, k: x * n + k + n*n
        col = lambda x, y, k: y * n + k + n*n*2
        box = lambda x, y, k: ((x // m) * m + (y // m)) * n + k + n*n*3
        idx = lambda x, y, k: (x * n + y) * n + k
        def link_row(a, b, c, d):
            a.l, b.l, c.l, d.l = d, a, b, c
            a.r, b.r, c.r, d.r = b, c, d, a
        def create(x, y, k):
            p = Cell(x=idx(x, y, k), y=pos(x, y, k), c=a[pos(x, y, k)])
            r = Cell(x=idx(x, y, k), y=row(x, y, k), c=a[row(x, y, k)])
            c = Cell(x=idx(x, y, k), y=col(x, y, k), c=a[col(x, y, k)])
            b = Cell(x=idx(x, y, k), y=box(x, y, k), c=a[box(x, y, k)])
            link_row(p, r, c, b)
        for i in range(n):
            for j in range(n):
                if grid[i][j] == 0:
                    for k in range(n):
                        create(i, j, k)
                else:
                    create(i, j, grid[i][j]-1)
        return cls(h)

def soduku(grid):
    grid = [i[:] for i in grid]
    n = len(grid)
    d = DancingLinks.from_sudoku(grid)
    a = d.run()[0]
    for i in a:
        r = i[1]
        k = r % n
        y = (r // n) % n
        x = ((r // n) // n) % n
        grid[x][y] = k + 1
    return grid

def nextline():
    s = input().strip()
    if len(s) == 0:
        return nextline()
    else:
        return s

def soduko9():
    def input_grid():
        grid = []
        for i in range(9):
            grid.append([])
            for j in nextline():
                grid[-1].append(int(j))
        return grid

    def output_grid(grid):
        for i in grid:
            for j in i:
                print(j, end='')
            print("")

    cas = int(input())
    for c in range(cas):
        output_grid(soduku(input_grid()))

def soduko16():
    def input_grid():
        grid = []
        for i in range(16):
            grid.append([])
            for j in nextline():
                grid[-1].append(ord(j)-ord('A')+1 if j != '-' else 0)
        return grid

    def output_grid(grid):
        for i in grid:
            for j in i:
                print(chr(ord('A')+j-1), end='')
            print("")
        print("")

    while True:
        try:
            output_grid(soduku(input_grid()))
        except EOFError:
            exit(0)

if __name__ == '__main__':
    # soduko9()
    # soduko16()

参考资料

跳跃的舞者，舞蹈链（Dancing Links）算法——求解精确覆盖问题
算法实践——舞蹈链（Dancing Links）算法求解数独
Github mharrys/sudoku