二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
插入
在二叉搜索树中插入新元素时,必须先检测该元素是否在树中已经存在。如果已经存在,则不进行插入;
否则将新元素加入到搜索停止的地方。
删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情况:
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
情况1可以归类到2或者3
对于上述情况,相应的删除方法如下:
a. 直接删除该结点
b. 删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点
c. 删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点
d. 在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,在来处理该结点的删除问题
二叉搜索树性能分析
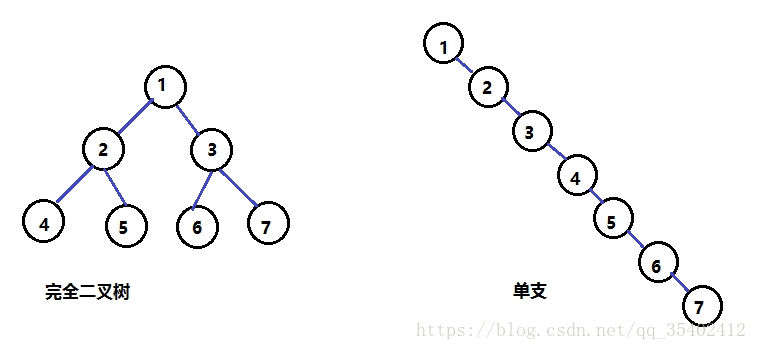
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。 对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多 ,但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树 。
最优情况下,二叉搜索树为完全二叉树,其平均比较次数为: logN
最差情况下,二叉搜索树退化为单支树,其平均比较次数为: N/2
class SNode{
private int key;
private String value;
private SNode left;
private SNode right;
public SNode(int key, String value){
this.key = key;
this.value = value;
}
public void setKey(int key){
this.key = key;
}
public int getKey(){
return this.key;
}
public void setValue(String value){
this.value = value;
}
public String getValue(){
return this.value;
}
public void setLeft(SNode left){
this.left = left;
}
public SNode getLeft(){
return this.left;
}
public void setRight(SNode right){
this.right = right;
}
public SNode getRight(){
return this.right;
}
}
public class SearchBTree{
public SNode root;
//有参构造方法,初始化root
public SearchBTree(int key, String value){
this.root = new SNode(key,value);
}
//创建一个结点
public SNode buySNode(int key, String value){
SNode node = new SNode(key,value);
return node;
}
//插入节点
public SNode insertSNodeR(SNode node, int key, String value){
if(node==null){
node = buySNode(key,value);
return node;
}
if(key<node.getKey()){
node.setLeft( insertSNodeR(node.getLeft(),key,value));
}
else if(key>node.getKey()){
node.setRight(insertSNodeR(node.getRight(),key,value));
}
return node;
}
//查找结点
public SNode findSNodeR(SNode root, int key){
if(root==null){
return null;
}
if(key<root.getKey()){
return findSNodeR(root.getLeft(),key);
}
else if(key>root.getKey()){
return findSNodeR(root.getRight(),key);
}
else{
return root;
}
}
//删除节点
public SNode removeSNodeR(SNode root, int key){
if(null==root){
return null;
}
if(key<root.getKey())
root.setLeft(removeSNodeR(root.getLeft(),key));
else if(key>root.getKey())
root.setRight(removeSNodeR(root.getRight(),key));
else{
SNode cur = root;
if(root.getLeft()==null){
return cur.getRight();
}
else if(root.getRight()==null){
return cur.getLeft();
}
else{
SNode parent = cur;
SNode sub = cur.getRight();
while(sub.getLeft()!=null){
sub=sub.getLeft();
}
cur.setKey(sub.getKey());
cur.setValue(sub.getValue());
removeSNodeR(cur.getRight(),key);
}
}
return root;
}
public void prevOrderR(SNode node){
if(node==null)
return;
System.out.print(node.getValue()+" ");
prevOrderR(node.getLeft());
prevOrderR(node.getRight());
}
public void inOrderR(SNode node){
if(node==null)
return;
inOrderR(node.getLeft());
System.out.print(node.getValue()+" ");
inOrderR(node.getRight());
}
public void postOrderR(SNode node){
if(node==null)
return;
postOrderR(node.getLeft());
postOrderR(node.getRight());
System.out.print(node.getValue()+" ");
}
public static void main(String[] agrs){
SearchBTree sTree = new SearchBTree(6,"F");//这里root需要先初始化,否则下列方法sTree.root无法引用传递
sTree.insertSNodeR(sTree.root,7,"G");
sTree.insertSNodeR(sTree.root,4,"D");
sTree.insertSNodeR(sTree.root,5,"E");
sTree.insertSNodeR(sTree.root,2,"B");
sTree.insertSNodeR(sTree.root,9,"I");
sTree.insertSNodeR(sTree.root,1,"A");
sTree.insertSNodeR(sTree.root,8,"H");
sTree.insertSNodeR(sTree.root,8,"Q");
sTree.insertSNodeR(sTree.root,3,"C");
System.out.print("先序遍历:");
sTree.prevOrderR(sTree.root);
System.out.print("
中序遍历:");
sTree.inOrderR(sTree.root);
System.out.print("
后序遍历:");
sTree.postOrderR(sTree.root);
System.out.println();
System.out.println("Find 7:"+sTree.findSNodeR(sTree.root,7).getValue());//这里我知道7和6肯定能找到,打印key
System.out.println("Find 6:"+sTree.findSNodeR(sTree.root,6).getValue());
System.out.println("Find 0:"+sTree.findSNodeR(sTree.root,0));//0和10本身就不在树里,会返回null指针,不可调用方法,否则运行时会报空指针错
System.out.println("Find 10:"+sTree.findSNodeR(sTree.root,10));
sTree.removeSNodeR(sTree.root,0);
sTree.removeSNodeR(sTree.root,1);
sTree.removeSNodeR(sTree.root,3);
sTree.removeSNodeR(sTree.root,5);
sTree.removeSNodeR(sTree.root,11);
System.out.print("中序遍历:");
sTree.inOrderR(sTree.root);
System.out.println();
}
}

二叉搜索树应用
1. 判断一个单词是否拼写正确2. 请模拟实现一个简单的字典
3. log文件中有许多异常重复的IP地址,请统计出每个异常IP出现了多少次?
二叉搜索树的变形,只要将key, value的类型修改,代码稍作修改即可;
1.判断一个单词拼写是否正确,先将所有的单词插入二叉搜索树,然后查找,若能找到则为正确
2.将key改为String类型,用来保存英文单词,value保存对应的中文意思,根据字符编码比较,创建搜索二叉树
3.key表示IP,value表示出现的次数,每次找到相同的IP,让value++;
3种应用在我的另一篇博客用C代码实现:点击打开链接