本文参考自《剑指offer》一书,代码采用Java语言。
题目
写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。
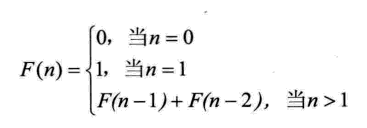
思路
如果直接写递归函数,由于会出现很多重复计算,效率非常底,不采用。
要避免重复计算,采用从下往上计算,可以把计算过了的保存起来,下次要计算时就不必重复计算了:先由f(0)和f(1)计算f(2),再由f(1)和f(2)计算f(3)……以此类推就行了,计算第n个时,只要保存第n-1和第n-2项就可以了。
测试用例
1.功能测试(3,5,8等)
2.边界值测试(0,1,2等)
3.性能测试(50,100等)
4.特殊(负数)
完整Java代码
(含测试代码)
/**
*
* @Description 斐波那契数列
*
* @author yongh
* @date 2018年9月13日 下午7:19:36
*/
// 题目:写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。
public class Fibonacci {
public long Fib(long n) {
if(n<0)
throw new RuntimeException("下标错误,应从0开始!");
if (n == 0)
return 0;
if (n == 1)
return 1;
long prePre = 0;
long pre = 1;
long result = 1;
for (long i = 2; i <= n; i++) {
result = prePre + pre;
prePre = pre;
pre = result;
}
return result;
}
//附:缩略版(考虑到代码的可读性,其实还是上面的方法比较好)
public long Fib2(long n) {
if(n<0)
throw new RuntimeException("下标错误,应从0开始!");
if (n == 0)
return 0;
if (n == 1)
return 1;
long pre = 0;
long result = 1;
for (long i = 2; i <= n; i++) {
result += pre;
pre = result - pre;
}
return result;
}
public static void main(String[] args) {
Fibonacci demo = new Fibonacci();
System.out.println(demo.Fib(0));
System.out.println(demo.Fib(1));
System.out.println(demo.Fib(2));
System.out.println(demo.Fib(8));
System.out.println(demo.Fib(50));
System.out.println(demo.Fib(100));
System.out.println(demo.Fib(-5));
}
}

0 1 1 21 12586269025 3736710778780434371 Exception in thread "main" java.lang.RuntimeException: 下标错误,应从0开始!
时间复杂度:O(n)
拓展
时间复杂度为O(longn)的解法
斐波那契数列有以下公式(可由数学归纳法推导得到):

由上式可知,求f(n),只需要对矩阵求(n-1)次方即可,但此时时间复杂度仍为O(n)。利用乘方的性质
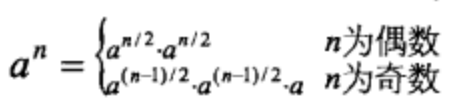
利用递归的思路计算乘方,即可将时间复杂度降低为O(longn)。这里给出对乘方函数的递归代码(引用):
Matrix2By2 MatrixPower(unsigned int n)
{
assert(n > 0);
Matrix2By2 matrix;
if(n == 1)
{
matrix = Matrix2By2(1, 1, 1, 0);
}
else if(n % 2 == 0)
{
matrix = MatrixPower(n / 2);
matrix = MatrixMultiply(matrix, matrix);
}
else if(n % 2 == 1)
{
matrix = MatrixPower((n - 1) / 2);
matrix = MatrixMultiply(matrix, matrix);
matrix = MatrixMultiply(matrix, Matrix2By2(1, 1, 1, 0));
}
return matrix;
}
青蛙跳台阶问题
题目1:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
将跳法总数记为f(n),可以知道f(1)=1,f(2)=2。当n>2时,第一次跳1级的话,还有f(n-1)种跳法;第一次跳2级的话,还有f(n-2)种跳法,所以可以推得f(n)=f(n-1)+f(n-2),即为斐波那契数列。
题目2:一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
解法1:
当n=1时,f(1)=1。
当n大于1时,归纳总结可知:跳上n级台阶,第一次跳1级的话,有f(n-1)种方法;第一次跳2级的话,有f(n-2)种方法……第一次跳n-1级的话,有f(1)种方法;直接跳n级的话,有1种方法,所以可以得到如下公式:
f(n) = f(n-1)+f(n-2)+......f(1)+1 (n≥2)
f(n-1) = f(n-2)+f(n-3)+.....f(1)+1 (n>2)
由上面两式相减可得,f(n)-f(n-1)=f(n-1),即f(n) = 2*f(n-1) (n>2)
最终结合f(1)和f(2),可以推得:f(n)=2^(n-1)
解法2:
假设跳到第n级总共需要k次,说明要在中间n-1级台阶中选出任意k-1个台阶,即C(n-1,k-1)种方法。
所以:跳1次就跳上n级台阶,需要C(n-1,0)种方法;跳2次需要C(n-1,1)种方法……跳n次需要C(n-1,n-1)种方法
总共需要跳C(n-1,0)+C(n-1,1)+C(n-1,2)+……C(n-1,n-1)=2^(n-1)种方法。
解法3:
除了必须到达最后一级台阶,第1级到第n-1级台阶都可以有选择的跳,也就是说对于这n-1个台阶来说,每个台阶都有跳上和不跳上2种情况,所以一共有2^(n-1)种方法。
矩形覆盖问题
题目:用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
当n = 1时,有一种方法。
当n = 2时,有两种方法。
当n >= 3时,和斐波那契数列类似。第一步竖着放,有f(n-1)种方法;第一步横着放,有f(n-2)种方法。所以f(n)=f(n-1)+f(n-2)。
收获
1.求n次方时,可以利用递归来降低时间复杂度
2.当遇到涉及n的问题时(类似青蛙跳台阶问题),不要紧张,可以进行归纳分析,特别注意f(n)与f(n-1)、f(n-2)等的关联,从而找出规律,进行合理建模。
3.return (int)Math.pow(2,target-1);
1) 转int类型
2)pow不是power
