SVD

SVD

 

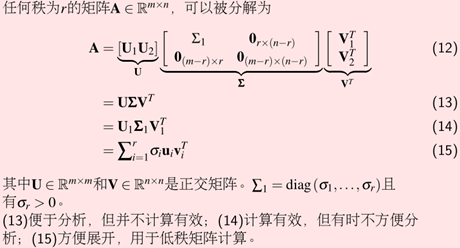
SVD和特征分解的关系：

 

如何计算SVD分解后U，V呢？

我们将A的转置和A做矩阵乘法，那么会得到n×n的一个方阵A^TA。既然A^TA是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：(A^TA)vi=λivi。这样我们就可以得到矩阵A^TA的n个特征值和对应的n个特征向量v了。将A^TA的所有特征向量张成一个n×n的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。

反过来我们将A和A的转置做矩阵乘法，将AA^T的所有特征向量张成一个m×m的矩阵V，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。

同时我们可以得到特征值矩阵等于奇异值矩阵的平方。

如何使用SVD进行降维呢？

注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？

假设我们的样本是m×n的矩阵X，如果我们通过SVD找到了矩阵XX^T最大的d个特征向量张成的m×d维矩阵U，则我们如果进行如下处理：

X_d×n′=U_d×m^TX_m×n

可以得到一个d×n的矩阵X′,这个矩阵和我们原来的m×n维样本矩阵X相比，行数从m减到了k，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。