Codeforces Round #415 (Div. 2) C. Do you want a date?

C. Do you want a date?

 

2 seconds

256 megabytes

 

Leha decided to move to a quiet town Vičkopolis, because he was tired by living in Bankopolis. Upon arrival he immediately began to expand his network of hacked computers. During the week Leha managed to get access to n computers throughout the town. Incidentally all the computers, which were hacked by Leha, lie on the same straight line, due to the reason that there is the only one straight street in Vičkopolis.

Let's denote the coordinate system on this street. Besides let's number all the hacked computers with integers from 1 to n. So the i-th hacked computer is located at the point xi. Moreover the coordinates of all computers are distinct.

Leha is determined to have a little rest after a hard week. Therefore he is going to invite his friend Noora to a restaurant. However the girl agrees to go on a date with the only one condition: Leha have to solve a simple task.

Leha should calculate a sum of F(a) for all a, where a is a non-empty subset of the set, that consists of all hacked computers. Formally, let's denote A the set of all integers from 1 to n. Noora asks the hacker to find value of the expression 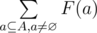. Here F(a) is calculated as the maximum among the distances between all pairs of computers from the set a. Formally, 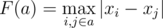. Since the required sum can be quite large Noora asks to find it modulo 109 + 7.

Though, Leha is too tired. Consequently he is not able to solve this task. Help the hacker to attend a date.

Input

The first line contains one integer n (1 ≤ n ≤ 3·105) denoting the number of hacked computers.

The second line contains n integers x1, x2, ..., xn (1 ≤ xi ≤ 109) denoting the coordinates of hacked computers. It is guaranteed that allxi are distinct.

Output

Print a single integer — the required sum modulo 109 + 7.

 

input

2
4 7

output

3

input

3
4 3 1

output

9

Note：

There are three non-empty subsets in the first sample test:,  and 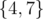. The first and the second subset increase the sum by 0and the third subset increases the sum by 7 - 4 = 3. In total the answer is 0 + 0 + 3 = 3.

There are seven non-empty subsets in the second sample test. Among them only the following subsets increase the answer: 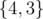, , 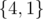, 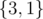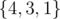. In total the sum is (4 - 3) + (4 - 1) + (3 - 1) + (4 - 1) = 9.

题目大意：

　　　　　输入一集合S，定义F（a）函数（a为S的非空子集），F（a）=a集合中最大值与最小值的差

　　　　　计算所有F(a)的和。

解题思路：

　　　　　因为要求最大值与最小值的差，所以首先想到的是把S集合排序 （a[j]-a[i]）*2^(j-i)

　　　　　对于只有一个元素的子集可以不用考虑 

　　　　　

　　　　　对于上面的式子

　　　　　最小值一共要被减去2^n-2^0次 也可以理解为加上2^0-2^n次

　　　　　最大值一共被加上2^n-2^0次  第i个元素被加了2^i-2^(n-i-1)

AC代码：

#include <stdio.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
const int mod = 1e9+7;
int a[300010];
__int64 b[300010];

using namespace std;

int main ()
{
    int n,i,j;
    while (~scanf("%d",&n))
    {
        b[1] = 1;
        for (i = 1; i <= n; i ++)
        {
            cin>>a[i];
            b[i+1] = b[i]*2%mod;   // 2^i  打表
        }
        sort(a+1,a+n+1);
        
        __int64 sum = 0;
        for (i = 1; i <= n; i ++)
        {
            sum += a[i]*(b[i]-b[n-i+1])%mod; // 直接代入公式
            sum %= mod;    
        }
        cout<<sum<<endl;
    }
    return 0;
}
            scanf("%d%d%d",&l,&r,&x);
            for(i = l; i <= r; i ++)
                if (p[i] < p[x])
                    sum ++;
            if (x-l == sum)
                printf("Yes
");
            else
                printf("No
");
        }
    }
    return 0;
}