无向图的点双联通分量

这是一个很重要也很容易搞混淆的概念，有必要画图解释一下。

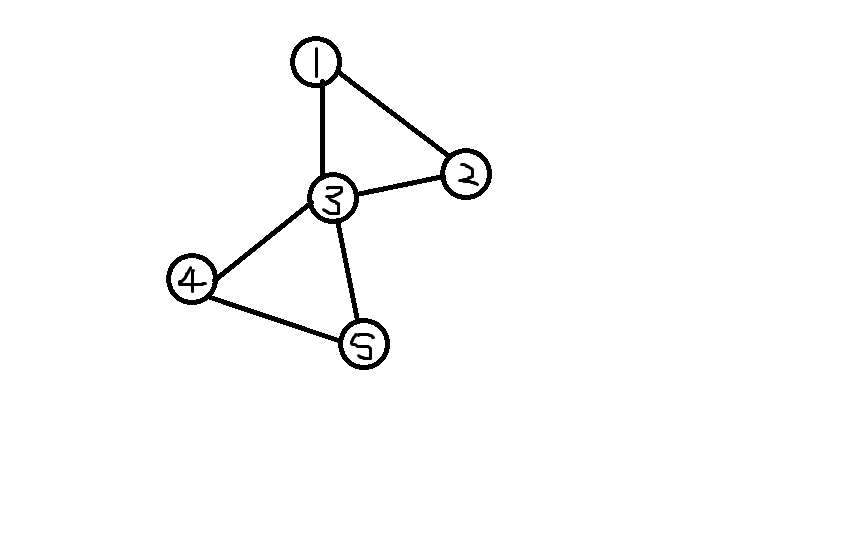
点双联通分量和边双联通分量的区别就在于，点双是指去掉“点”还能联通的子结构。边双是指去掉”边“还能联通的结构。

在上例中，{1,2,3,4,5}是边双，{1,2,3}和{3,4,5}是点双。

这篇文章讲讲怎么求点双，关键在于栈中存储的是边而不是点。（这是一个巨大的坑点，我曾经错过无数次，一直到了很后来才发现自己的模板错了。。。）

还是结合代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector> 
#include <stack>

using namespace std;

const int maxn = 105, maxm = maxn * 2;

int n, m, tot, dfs_clock, bcc_cnt;

int h[maxn], dfn[maxn], low[maxn], iscut[maxn], bccno[maxn];

vector<int> bcc[maxn];
 
struct edge1
{
    int v, next;
}a[maxm];

struct EDGE
{
    int u, v;
};

stack<EDGE> s;

void add(int x, int y)
{
    a[tot].v = y;
    a[tot].next = h[x];
    h[x] = tot++;
}

int dfs(int u, int fa)
{
    int lowu = dfn[u] = ++dfs_clock;
    int child = 0;
    for (int i = h[u]; ~i; i = a[i].next)
    {
        int v = a[i].v;
        EDGE e = (EDGE){u, v};//所谓栈中存储的是边
        if (!dfn[v])
        {
            s.push(e);//把沿途遍历到的边都加入栈
            child++;
            int lowv = dfs(v, u);
            lowu = min(lowu, lowv);
            if (lowv >= dfn[u])
            {
                iscut[u] = 1;//我们发现了一个割顶，也就说明当前栈中已经保存了一个点双的集合。
                bcc_cnt++;//bcc_cnt从1开始。
                bcc[bcc_cnt].clear();//应付多组数据，应该先清空。
                for(;;)
                {
                    EDGE x = s.top(); s.pop();
                    if (bccno[x.u] != bcc_cnt)
                    {
                        bcc[bcc_cnt].push_back(x.u);
                        bccno[x.u] = bcc_cnt;
                    }
                    if (bccno[x.v] != bcc_cnt)
                    {
                        bcc[bcc_cnt].push_back(x.v);
                        bccno[x.v] = bcc_cnt;
                    }//这两段的意思是，把边集中涉及到的点全部取出来，把他们的bccno[]设置成当前的bcc_cnt
                    if (x.u == u && x.v == v) break;//一直弹栈直到弹到了当前加入的边，break。
                }
            }
        }else if (dfn[v] < dfn[u] && v != fa)
        {
            s.push(e);//把沿途遍历到的边都加入栈。
            lowu = min(lowu, dfn[v]);
        }
    }
    if (fa == 0 && child == 1)
    {
        iscut[u] = 0;
    }
    low[u] = lowu;
    return lowu;
}

int main()
{
    freopen("无向图的点双联通分量.in","r",stdin);
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h); tot = dfs_clock = bcc_cnt = 0;
    for (int i = 1; i <= m; i++)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        add(x, y); add(y, x);
    }
    dfs(1, 0);
    for (int i = 1; i <= bcc_cnt; i++)
    {
        for (int j = 0; j < bcc[i].size(); j++)
            printf("%d ", bcc[i][j]);
        printf("
");
    }
    return 0;
}

因为割顶明显不可能属于任何一个点双，所以说割顶的bccno无意义。

明天写边双（其实就是第二次dfs不经过桥即可）和有向图的强连通分量SCC。

这些是图论的基础算法，一定要牢记。