介绍一下这道猛题编程题
一次二元方程的解题。a、b、c三个数的平方根。ax2+bx+c = 0,(现在在家用笔记本,没有单位电脑方便所以我就简单写一下题目)
我做的编程内容:
# Prompt three date number
a, b, c = eval(input("Enter a,
b, c: "))
# Model number method
dateNumber = (b ** 2 - 4 * a * c) ** 0.5
print(f"dateNumber {dateNumber}")
r1 = round((-b + dateNumber) / 2 * a, 6)
r2 = round((-b - dateNumber) / 2 * a, 6)
if dateNumber > 0:
print(f"The roots
are {r1} and {r2}")
elif dateNumber == 0:
print("The root
is -1")
else:
print("The
equation has no real roots")
按要求我输入了三组数
1,3,1、
1,2,1、
1,2,3
经过学习呢确实有自己的一些解题的感觉了。我输入了前两组得到了跟书中要求的答案。但第三组数1,2,3出现后崩溃开始了
下面是出错的内容:
Traceback (most recent call last):
File "C:/Users/apple/20200225/04-00 contest.py", line 9, in <module>
r1 = round((-b + dateNumber) / 2 * a, 6)
TypeError: type complex doesn't define __round__ method
凭着我的野蛮英语 我猜测在round方面的问题。可是改了几遍发现没有什么作用,而且自己还想到第1组、第2组也是这个公式都OK呀,那个时候round都没有变化,所以排除了round的问题。接着上网搜索吧。某狗浏览器。我真的不想用了。用了度娘。但这个错误提示估计太偏僻了也没有不对。最后选择了Error的几个单词。我明白了原来是所谓的数据根本不是round能处理的。我估计是不是这算溢出呢。(对溢出这个词的理解)
既然知道了问题,那么继续解决。不断的犯错才能不断的进步。犯错不怕,可怕的是放不下放错的道德标准。(刚想到的意义)
每次遇到问题我都会想办法,比如用打印结果来慢慢验证。程序里有一个变量dateNumber((b ** 2) - (4 * a * c)) 根据题里的介绍整个程序判定也是判断dateNumber正、负或0 来进行完成的。
三组数据输出如下:
第一组
Enter a, b, c: 1,3,1
dateNumber 2.23606797749979
The roots are -0.381966 and -2.618034
第二组
Enter a, b, c: 1,2,1
dateNumber 0.0
The root is -1
第三组,各位接下来就是见证奇迹的时刻!
Enter a, b, c: 1,2,3
dateNumber (1.7319121124709868e-16+2.8284271247461903j)
大家看一眼,哇塞滴呀,各位兄弟姐妹们,这个是什么鬼!!!
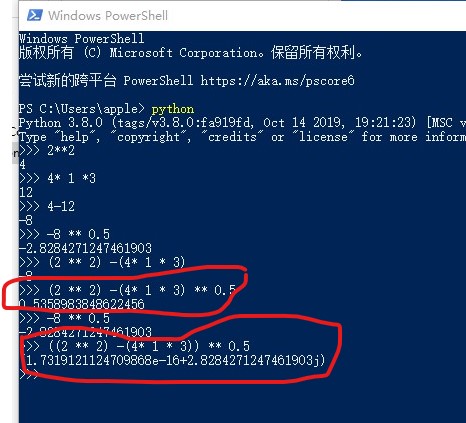
我后来用了windows powershell里打开了python,用第3组数手动玩一下dateNumber公式,(**在这里我没有用math的功能然后平方的时候我喜欢用b ** 2)
(b ** 2 - 4 * a * c) ** 0.5
结果是-2.8284271247461903 可是我们用Pycharm运行后却变成了出错,vcode也是一模一样。
我拿出了我上一次做的编程来比对
# 4.1 compute roots
a, b, c = eval(input("Enter a, b, c integer: "))
# mathematical formula
r1 = (-b + ((b ** 2) - (4 * a * c)) ** 0.5) / (2 * a)
r2 = (-b - ((b ** 2) - (4 * a * c)) ** 0.5) / (2 * a)
if (b ** 2) - (4 * a * c) > 0:
print("The roots are", r1, "and", r2)
if (b ** 2) - (4 * a * c) == 0:
print("The root is", r1 or r2)
else:
print("The equation has no real roots")
这是我上次做的竟然通过了
那么这个问题在哪里呢???
上一次的编程里我没有单独设立dateNumber这样的变量而是直接将公式做为if里的判定,于是我参考上一次编程时写的方式重写了下方公式
又做了一次尝试,我将dateNumber的公式改为
dateNumber = (b ** 2) - (4 * a * c) ** 0.5
用了两个括号将两个元素分别开来计算。结果呢
Enter a, b, c: 1,2,3
dateNumber 0.5358983848622456
The roots are -0.732051 and -1.267949
但正常应该是显示The equation has no real root
而-8开平方的结果应该是-2.8284271247481903
接着看到上次程序里并没有带上** 0.5在公式里。疑问继续在增加并没有减少。接着我尝试的去掉了** 0.5 直接运行(b ** 2) - (4 * a * c) 结果是-8和之前的计算符合。这也变相的发现了上次我这道题通过的是-8来判定成了没根。而不是用-8的开平方来作为if语句判断的数据。不过不带开平方的也是题本身要求的。
接下来继续尝试用PoweShell里执行python来计算发现了为什么会出现0.5358983848622456,原来是运算顺序决定的。我没把(b**2)-(4*1*3)放在一个括号里。那么python根据设置好的运行顺序最终得出了0.5…..这样的数据。那我接着就把他们放在一个括号里。结果呢(看下图第2个圈)
6月5日接着6月4日的战斗继续。换了一台机器。没有用中文插件。
并且我调用了math里的sqrt。结果1,2,3,哇塞真是魔性。
另外今天对这个程序第二个判断做了一个小修改到很意外的不错
print(f"The root is {r1 or r2}")
显示的结果跟答案要求的一样。看来每一次重写程序,就和写作文不断修改一样会有新发现
不说了,再说用昨天的方法换机器后的状态
a, b, c = eval(input("Enter a,b,c: "))
# 根据题的介绍得出所谓公式为(b ** 2 - 4 * a *c) ** 0.5 变量名为dateN
dateNumber =(b ** 2 - 4 * a * c) ** 0.5
dateNumber用了昨天的写法。结果。继续,这回是新错误。新错误就是我的新朋友。数据之间不支持。
那我再次打印吧,打印的结果和昨天一样
F:ProgramDataAnaconda3python.exe "F:/LearnPython/untitled/04-00 contest.py"
Enter a,b,c: 1,2,3
dateNumber is (1.7319121124709868e-16+2.8284271247461903j)(和另一台机器一样。)
Traceback (most recent call last):
File "F:/LearnPython/untitled/04-00 contest.py", line 15, in <module>
if dateNumber > 0:
TypeError: '>' not supported between instances of 'complex' and 'int'
为什么 1,3,1 和1,2,1都没问题。? 到123完蛋了。为什么1,2,3开平方变成了
“1.7319121124709868e-16+2.8284271247461903j” 大哥你代表什么