一、实验目的
科学技术中常常要求解常微分方程的定解问题,所谓数值解法就是求未知函数在一系列离散点处的近似值。
二、实验原理

三、实验程序
1. 尤拉公式程序

2、3、4的尤拉公式的程序参上改写。
四、实验内容

五、实验代码及运行结果
• MATLAB代码:
定义函数:
function [A1,A2,B1,B2,C1,C2]=euler23(a,b,n,y0)
%欧拉法解一阶常微分方程
%初始条件y0
h = (b-a)/n; %步长h
%区域的左边界a
%区域的右边界b
x = a:h:b;
m=length(x);
%前向欧拉法
y = y0;
for i=2:m
y(i)=y(i-1)+h*oula(x(i-1),y(i-1));
A1(i)=x(i);
A2(i)=y(i);
end
plot(x,y,'r-');
hold on;
%改进欧拉法
y = y0;
for i=2:m
y(i)= y(i-1)+h/2*( oula(x(i-1),y(i-1))+oula(x(i),y(i-1))+h*(oula(x(i-1),x(i-1))));
B1(i)=x(i);
B2(i)=y(i);
end
plot(x,y,'m-');
hold on;
%欧拉两步公式
y=y0;
y(2)=y(1)+h*oula(x(1),y(1));
for i=2:m-1
y(i+1)=y(i-1)+2*h*oula(x(i),y(i));
C1(i)=x(i);
C2(i)=y(i);
end
plot(x,y,'b-');
hold on;
%精确解用作图
xx = x;
f = dsolve('Dy=-y+1','y(0)=0','x');%求出解析解
y = subs(f,xx); %将xx代入解析解,得到解析解对应的数值
plot(xx,y,'k--');
legend('前向欧拉法','改进欧拉法','欧拉两步法','解析解');
function f=oula(x,y)
f=-y+1;
命令行窗口:
[A1,A2,B1,B2,C1,C2]=euler23(0,1,10,0)
运行结果:
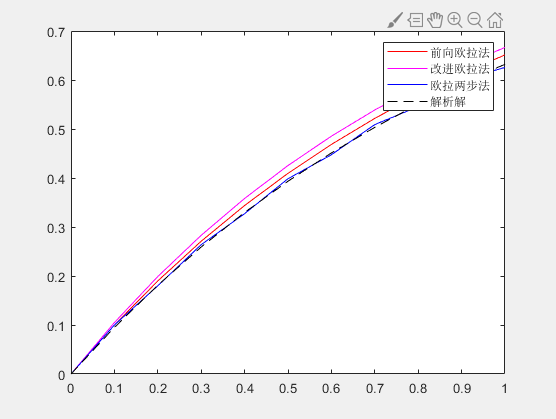
N=50时:
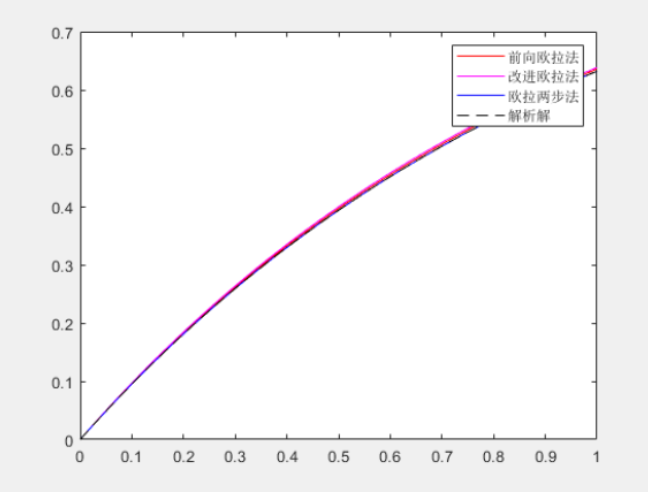
N=100时:

故得精度越大时,几种方法求解值与准确值越来越接近。
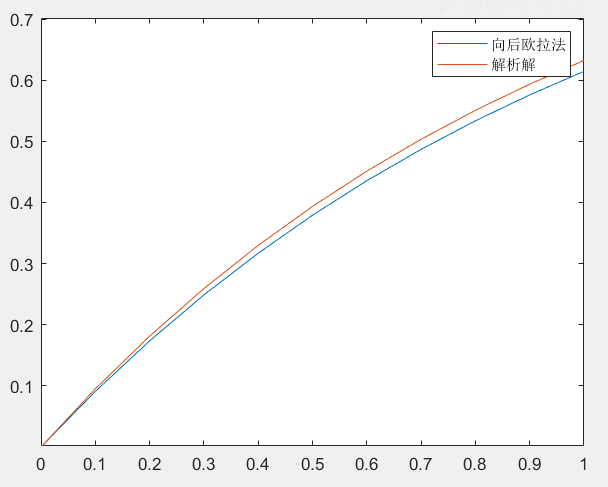
• 另解
clear;
format long;
a = 0;
b = 1;
h = 0.1;
d = 0;
res = forward(a, b, h, d);
x = res(1,:);
y = res(2,:);
xx = x;
f = dsolve('Dy=-y+1','y(0)=0','x');
z = subs(f,xx);
y(2,:) = z;
plot(x, y);
function result = forward(a, b, h, y)
n = (b-a)/h;
x0 = a;
x1 = a;
y0 = y;
result(1,1) = x0;
result(2,1) = y0;
for m = 0:n-1
x1 = x1 + h;
f0 = 1-y0;
d = y0 + h*f0;
y1 = calculate(y0, x1, d, h);
%result = calculate(x1, d, h);
x0 = x1;
y0 = y1;
result(1, m+2) = x0;
result(2, m+2) = y0;
end
end
function result = calculate(y0, x1, y1, h)
acc = -6;
now = 0.0;
z1 = y1;
while now >= -6
z0 = z1;
f0 =1-z0;
z1 = y0 + h*f0;
now = log10(abs(z1-z0));
end
result = z1;
end
运行结果: