数值计算方法实验之Hermite 多项式插值 (Python 代码)

一、实验目的

  在已知f(x),x∈[a,b]的表达式，但函数值不便计算,或不知f(x),x∈[a,b]而又需要给出其在[a,b]上的值时，按插值原则f(x_i)= y_i(i= 0,1…….,n)求出简单函数P(x)(常是多项式),使其在插值基点x_i,处成立P(x_i)= y_i(i=0,1,……,n),而在[a,b]上的其它点处成立f(x)≈P(x).

二、实验原理

 

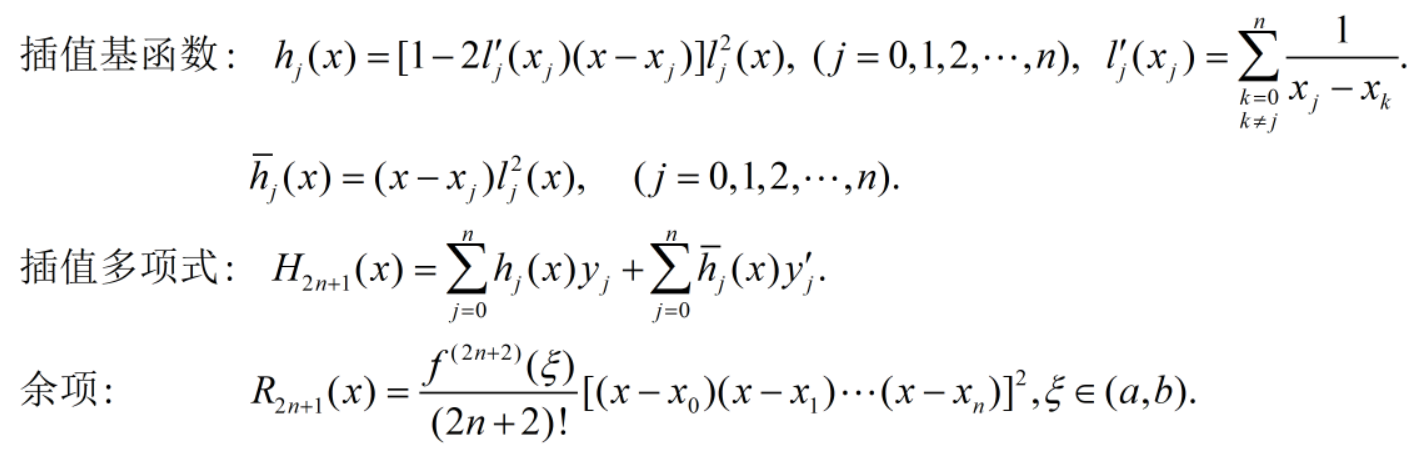
 三、实验内容

  求f(x)=x⁴在[0,2]上按5个等距节点确定的Hermite插值多项式.

四、实验程序

import numpy as np
from sympy import *
import matplotlib.pyplot as plt


def f(x):
    return  x ** 4


def ff(x):  # f[x0, x1, ..., xk]
    ans = 0
    for i in range(len(x)):
        temp = 1
        for j in range(len(x)):
            if i != j:
                temp *= (x[i] - x[j])
        ans += f(x[i]) / temp
    return ans


def draw(L, newlabel= 'Lagrange插值函数'):
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    x = np.linspace(0, 2, 100)
    y = f(x)
    Ly = []
    for xx in x:
        Ly.append(L.subs(n, xx))
    plt.plot(x, y, label='原函数')
    plt.plot(x, Ly, label=newlabel)
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()

    plt.savefig('1.png')
    plt.show()


def lossCal(L):
    x = np.linspace(0, 2, 101)
    y = f(x)
    Ly = []
    for xx in x:
        Ly.append(L.subs(n, xx))
    Ly = np.array(Ly)
    temp = Ly - y
    temp = abs(temp)
    print(temp.mean())


def calM(P, x):
    Y =   n ** 4
    dfP = diff(P, n)
    return solve(Y.subs(n, x[0]) - dfP.subs(n, x[0]), [m,])[0]


if __name__ == '__main__':
    x = np.array(range(11)) - 5
    y = f(x)

    n, m = symbols('n m')
    init_printing(use_unicode=True)

    P = f(x[0])
    for i in range(len(x)):
        if i != len(x) - 1:
            temp = ff(x[0:i + 2])
        else:
            temp = m
        for j in x[0:i + 1]:
            temp *= (n - j)
        P += temp
    P = expand(P)

    P = P.subs(m, calM(P, x))
    draw(P, newlabel='Hermite插值多项式')
    lossCal(P)

五、运算结果