学习大佬:树的直径求法及证明
树的直径
定义:
一棵树的直径就是这棵树上存在的最长路径。
给定一棵树,树中每条边都有一个权值,树中两点之间的距离定义为连接两点的路径边权之和。树中最远的两个节点之间的距离被称为树的直径,连接这两点的路径被称为树的最长链。后者通常也可称为直径,即直径是一个数值概念,也可代指一条路径。
求法:
一、树形dp
时间复杂度:O( n );
优点:代码量少实现方便。
不足:不容易记录路径。
实现过程:
状态:d[ x ] 以当前结点 x 为根的 子树的直径。
我们枚举每一个结点 x 以及 它要到达的下一个结点 Eiv。
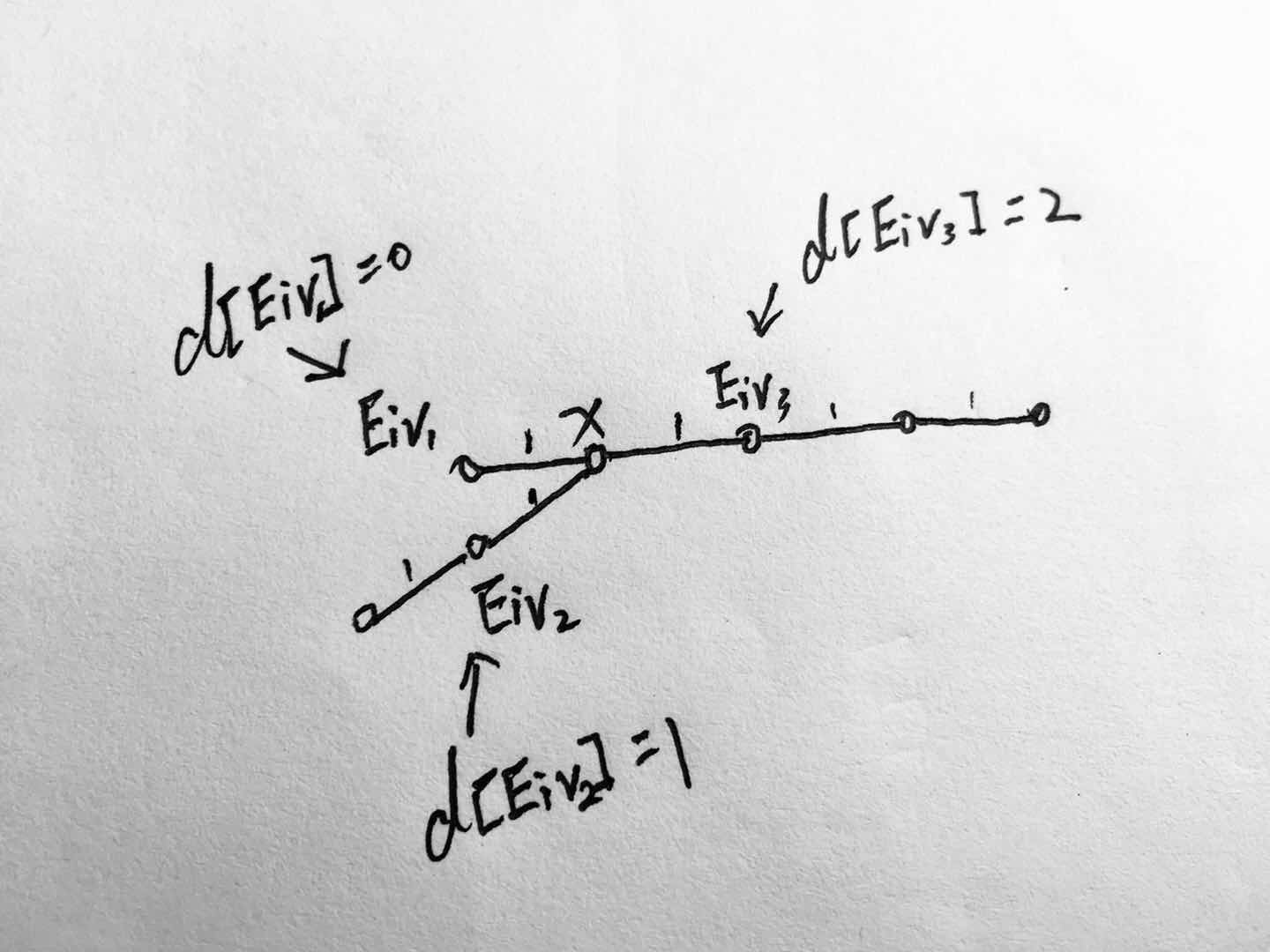
这两个结点所能达到的最大距离之和 加上 这两个结点的边权就有可能去更新树的直径。
即:树的直径 ans_max = max{ d[ x ] + d[ Eiv ] + edge[x, Eiv] } (1 <= x <= N)
那么 d[ x ] 通过什么更新呢?当然是由 它所连接下一个结点所能达到最大距离 来更新了;
即 d[ x ] = max{ d[ x ], d[ Eiv ] + edge[ x, Eiv ] };
核心代码:
1 void dp(int st) 2 { 3 vis[st] = true; //当前结点已访问 4 for(int i = head[st]; i != -1; i = edge[i].nxt){ 5 int Eiv = edge[i].v; 6 if(vis[Eiv]) continue; //不走回头路 7 dp(Eiv); 8 ans_max = max(ans_max, d[st] + d[Eiv] + edge[i].w); //更新树的直径(由当前结点两段之和更新) 9 d[st] = max(d[st], d[Eiv]+edge[i].w); //更新当前结点所能走的最长路径(保留较长的那边) 10 } 11 }
二、DFS || BFS
时间复杂度: O( n );
优点:可以在第一次 dfs/bfs记录前驱
不足:代码量稍大
实现过程:
前提:
两次dfs或bfs。第一次任意选一个点进行dfs(bfs)找到离它最远的点,此点就是最长路的一个端点,再以此点进行dfs(bfs),找到离它最远的点,此点就是最长路的另一个端点,于是就找到了树的直径。
证明(by大佬):
假设此树的最长路径是从s到t,我们选择的点为u。反证法:假设搜到的点是v。
1、v在这条最长路径上,那么dis[u,v]>dis[u,v]+dis[v,s],显然矛盾。
2、v不在这条最长路径上,我们在最长路径上选择一个点为po,则dis[u,v]>dis[u,po]+dis[po,t],那么有dis[s,v]=dis[s,po]+dis[po,u]+dis[u,v]>dis[s,po]+dis[po,t]=dis[s,t],即dis[s,v]>dis[s,t],矛盾。
也许你想说u本身就在最长路径,或则其它的一些情况,但其实都能用类似于上面的反证法来证明的。
综上所述,你两次dfs(bfs)就可以求出最长路径的两个端点和路径长度。
核心代码:
1 void dfs(int s) 2 { 3 for(int i = head[s]; i != -1; i = edge[i].nxt){ 4 int Eiv = edge[i].v; 5 if(fa[s] == Eiv) continue; //不走回头路,也可以递归父亲结点省去fa数组空间 6 fa[Eiv] = s; 7 dis[Eiv] = dis[s] + edge[i].w; //当前结点最长路径 8 dfs(Eiv); 9 } 10 }
三、举栗子
Cow Marathon
| Time Limit: 2000MS | Memory Limit: 30000K | |
| Total Submissions: 6925 | Accepted: 3279 | |
| Case Time Limit: 1000MS | ||
Description
Input
Output
Sample Input
7 6 1 6 13 E 6 3 9 E 3 5 7 S 4 1 3 N 2 4 20 W 4 7 2 S
Sample Output
52
Hint
题意概括:
建一颗 N 个节点 M 条边的树,求树上两点最长距离(树的直径);方向都是虚的,建双向边。
解题思路:
①树形dp
AC code:

1 //树形dp版 2 #include <cstdio> 3 #include <iostream> 4 #include <algorithm> 5 #include <cstring> 6 #include <vector> 7 #define INF 0x3f3f3f3f 8 using namespace std; 9 const int MAXN = 5e4+5; 10 int d[MAXN]; 11 bool vis[MAXN]; 12 int head[MAXN], cnt; 13 int N, M, ans_max; 14 struct Edge 15 { 16 int v, w, nxt; 17 Edge(int _v = 0, int _w = 0, int _nxt = 0):v(_v), w(_w), nxt(_nxt){}; 18 }edge[MAXN<<1]; 19 20 void init() 21 { 22 memset(head, -1, sizeof(head)); 23 memset(d, 0, sizeof(d)); 24 memset(vis, false, sizeof(vis)); 25 cnt = 0; 26 } 27 28 void AddEdge(int from, int to, int weight) 29 { 30 edge[cnt] = Edge(to, weight, head[from]); 31 head[from] = cnt++; 32 } 33 34 void dp(int st) 35 { 36 vis[st] = true; //当前结点已访问 37 for(int i = head[st]; i != -1; i = edge[i].nxt){ 38 int Eiv = edge[i].v; 39 if(vis[Eiv]) continue; //不走回头路 40 dp(Eiv); 41 ans_max = max(ans_max, d[st] + d[Eiv] + edge[i].w); //更新树的直径(由当前结点两段之和更新) 42 d[st] = max(d[st], d[Eiv]+edge[i].w); //更新当前结点所能走的最长路径(保留较长的那边) 43 } 44 } 45 46 int main() 47 { 48 while(~scanf("%d%d", &N, &M)) 49 { 50 init(); 51 char ccc; 52 for(int i = 1, u, v, w; i <= M; i++){ 53 scanf("%d%d%d %c", &u, &v, &w, &ccc); 54 AddEdge(u, v, w); 55 AddEdge(v, u, w); 56 } 57 //printf("%d ", ans); 58 ans_max = 0; 59 dp(1); 60 printf("%d ", ans_max); 61 } 62 return 0; 63 }
②两次DFS
AC code:

1 //DFS版 2 /* 3 #include <cstdio> 4 #include <iostream> 5 #include <algorithm> 6 #include <cstring> 7 #include <vector> 8 #define INF 0x3f3f3f3f 9 using namespace std; 10 const int MAXN = 5e4+5; 11 int dis[MAXN], fa[MAXN]; 12 int head[MAXN], cnt; 13 int N, M, ans; 14 15 struct Edge 16 { 17 int v, w, nxt; 18 Edge(int _v = 0, int _w = 0, int _nxt = 0):v(_v), w(_w), nxt(_nxt){}; 19 }edge[MAXN<<1]; 20 21 void AddEdge(int from, int to, int weight) 22 { 23 edge[cnt] = Edge(to, weight, head[from]); 24 head[from] = cnt++; 25 } 26 27 void init() 28 { 29 memset(head, -1, sizeof(head)); 30 for(int i = 0; i <= N; i++) fa[i] = i; 31 cnt = 0; 32 ans = 0; 33 } 34 35 void dfs(int s) 36 { 37 for(int i = head[s]; i != -1; i = edge[i].nxt){ 38 int Eiv = edge[i].v; 39 if(fa[s] == Eiv) continue; //不走回头路,也可以递归父亲结点省去fa数组空间 40 fa[Eiv] = s; 41 dis[Eiv] = dis[s] + edge[i].w; //当前结点最长路径 42 dfs(Eiv); 43 } 44 } 45 46 int main() 47 { 48 while(~scanf("%d%d", &N, &M)) 49 { 50 init(); 51 char ccc; 52 for(int i = 1, u, v, w; i <= M; i++){ 53 scanf("%d%d%d %c", &u, &v, &w, &ccc); 54 AddEdge(u, v, w); 55 AddEdge(v, u, w); 56 } 57 //printf("%d ", ans); 58 int ans_max = 0, ans_index = 0; 59 dfs(1); //第一次dfs找出树的直径所在的点 60 for(int i = 1; i <= N; i++){ 61 if(dis[i] > ans_max){ 62 ans_max = dis[i]; 63 ans_index = i; 64 } 65 dis[i] = 0; 66 fa[i] = i; 67 } 68 69 dfs(ans_index); //第二次dfs找出树的直径 70 for(int i = 1; i <= N; i++){ 71 if(dis[i] > ans_max) ans_max = dis[i]; 72 } 73 printf("%d ", ans_max); 74 } 75 return 0; 76 }
Caterpillar
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 2505 | Accepted: 1180 |
Description
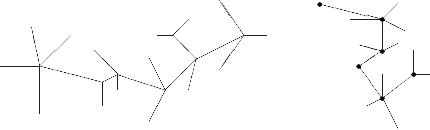
An undirected graph is called a caterpillar if it is connected, has no cycles, and there is a path in the graph where every node is either on this path or a neighbor of a node on the path. This path is called the spine of the caterpillar and the spine may not be unique. You are simply going to check graphs to see if they are caterpillars.
For example, the left graph below is not a caterpillar, but the right graph is. One possible spine is
shown by dots.
Input
There will be multiple test cases. Each test case starts with a line containing n indicating the number of nodes, numbered 1 through n (a value of n = 0 indicates end-of-input). The next line will contain an integer e indicating the number of edges. Starting on the following line will be e pairs n1 n2 indicating an undirected edge between nodes n1 and n1. This information may span multiple lines. You may assume that n ≤ 100 and e ≤ 300. Do not assume that the graphs in the test cases are connected or acyclic.
Output
For each test case generate one line of output. This line should either be
Graph g is a caterpillar.or
Graph g is not a caterpillar.
as appropriate, where g is the number of the graph, starting at 1.
Sample Input
22 21 1 2 2 3 2 4 2 5 2 6 6 7 6 10 10 8 9 10 10 12 11 12 12 13 12 17 18 17 15 17 15 14 16 15 17 20 20 21 20 22 20 19 16 15 1 2 2 3 5 2 4 2 2 6 6 7 6 8 6 9 9 10 10 12 10 11 10 14 10 13 13 16 13 15 0
Sample Output
Graph 1 is not a caterpillar. Graph 2 is a caterpillar.
题意概括:
首先需要判断给的图是不是一棵树;
其次需要判断是否存在一条路径使得图上所有的点要么在这条路径上,要么距离该路径的距离为 1。
解题思路:
判断是否为一棵树直接dfs判断是否存在环即可;
为了让最多的点满足第二个条件,则这条路径一定是树的直径。
两次DFS求出树的直径,遍历一遍判断是否所有点都满足条件。
为了做这个判断,DFS时不仅要更新树的直径还要同时更新每一个结点能达到的最长路径;
如果当前结点能达到的最长路径等于树的直径说明该结点在树的直径上,如果不能则判断他是否能通过相连的结点到达树的直径。
AC code:

1 #include <bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 using namespace std; 4 const int MAXN = 300; 5 struct Edge{int v; int nxt;}edge[MAXN<<1]; 6 int head[MAXN], cnt; 7 int dis[MAXN], bb[MAXN]; 8 bool vis[MAXN]; 9 int N, M; 10 int ans_max, ans_index; 11 bool chck; 12 13 void init() 14 { 15 memset(head, -1, sizeof(head)); 16 memset(vis, false, sizeof(vis)); 17 memset(dis, 0, sizeof(dis)); 18 memset(bb, 0, sizeof(bb)); 19 cnt = 0; 20 chck = false; 21 ans_max = 0; ans_index = 0; 22 } 23 24 void AddEdge(int from, int to) 25 { 26 edge[cnt].v = to; 27 edge[cnt]. nxt = head[from]; 28 head[from] = cnt++; 29 } 30 31 void check(int s, int fa) 32 { 33 vis[s] = true; 34 for(int i = head[s]; i != -1; i = edge[i].nxt){ 35 int Eiv = edge[i].v; 36 if(Eiv == fa) continue; 37 if(vis[Eiv]) {chck = true; return;} 38 check(Eiv, s); 39 if(chck) return; 40 } 41 } 42 43 void dfs(int s, int fa) 44 { 45 for(int i = head[s]; i != -1; i = edge[i].nxt){ 46 int Eiv = edge[i].v; 47 if(Eiv != fa){ 48 dis[Eiv] = dis[s] + 1; 49 bb[Eiv] = dis[Eiv]; 50 if(dis[Eiv] > ans_max) {ans_max = dis[Eiv]; ans_index = Eiv;} //更新树的直径 51 dfs(Eiv, s); 52 bb[s] = max(bb[s], bb[Eiv]); //更新当前结点最长路径 53 } 54 } 55 } 56 57 int main() 58 { 59 int T_case = 0; 60 while(~scanf("%d", &N) && N){ 61 scanf("%d", &M); 62 init(); 63 for(int m = 1, u, v; m <= M; m++){ 64 scanf("%d%d", &u, &v); 65 AddEdge(u, v); 66 AddEdge(v, u); 67 } 68 69 if(M > N-1) chck = true; 70 if(!chck) check(1, 0); //判断是否存在环 71 if(!chck){ 72 for(int i = 1; i <= N; i++){ 73 if(!vis[i]){chck = true; break;} //判断所有点是否联通 74 } 75 if(!chck){ 76 dis[1] = 0; 77 dfs(1, 0); //第一次dfs找出树的直径所在的点 78 dis[ans_index] = 0; 79 dfs(ans_index, 0); //第二次dfs找出树的直径 80 for(int i = 1; i <= N; i++){ //判断所有的点是否满足条件 81 bool flag = false; 82 if(bb[i] == ans_max) continue; //在直径上 83 for(int k = head[i]; k != -1; k = edge[k].nxt){ //判断不在树的直径上的点到树的直径距离是否为 1 84 if(bb[edge[k].v] == ans_max) {flag = true; break;} 85 } 86 if(!flag) {chck = true; break;} 87 } 88 } 89 } 90 if(chck) printf("Graph %d is not a caterpillar. ", ++T_case); 91 else printf("Graph %d is a caterpillar. ", ++T_case); 92 } 93 return 0; 94 }
