任意门:https://vjudge.net/problem/CodeForces-822D
D. My pretty girl Noora
In Pavlopolis University where Noora studies it was decided to hold beauty contest "Miss Pavlopolis University". Let's describe the process of choosing the most beautiful girl in the university in more detail.
The contest is held in several stages. Suppose that exactly n girls participate in the competition initially. All the participants are divided into equal groups, x participants in each group. Furthermore the number x is chosen arbitrarily, i. e. on every stage number x can be different. Within each group the jury of the contest compares beauty of the girls in the format "each with each". In this way, if group consists of x girls, then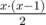 
comparisons occur. Then, from each group, the most beautiful participant is selected. Selected girls enter the next stage of the competition. Thus if n girls were divided into groups, x participants in each group, then exactly 
participants will enter the next stage. The contest continues until there is exactly one girl left who will be "Miss Pavlopolis University"
But for the jury this contest is a very tedious task. They would like to divide the girls into groups in each stage so that the total number of pairwise comparisons of the girls is as few as possible. Let f(n) be the minimal total number of comparisons that should be made to select the most beautiful participant, if we admit n girls to the first stage.
The organizers of the competition are insane. They give Noora three integers t, l and r and ask the poor girl to calculate the value of the following expression: t0·f(l) + t1·f(l + 1) + ... + tr - l·f(r). However, since the value of this expression can be quite large the organizers ask her to calculate it modulo 109 + 7. If Noora can calculate the value of this expression the organizers promise her to help during the beauty contest. But the poor girl is not strong in mathematics, so she turned for help to Leha and he turned to you.
The first and single line contains three integers t, l and r (1 ≤ t < 109 + 7, 2 ≤ l ≤ r ≤ 5·106).
In the first line print single integer — the value of the expression modulo 109 + 7.
2 2 4
19
Consider the sample.
It is necessary to find the value of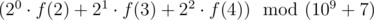 
.
f(2) = 1. From two girls you can form only one group of two people, in which there will be one comparison.
f(3) = 3. From three girls you can form only one group of three people, in which there will be three comparisons.
f(4) = 3. From four girls you can form two groups of two girls each. Then at the first stage there will be two comparisons, one in each of the two groups. In the second stage there will be two girls and there will be one comparison between them. Total 2 + 1 = 3 comparisons. You can also leave all girls in same group in the first stage. Then 
comparisons will occur. Obviously, it's better to split girls into groups in the first way.
Then the value of the expression is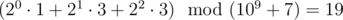 
题意概括：
有N个人参加选美比赛，可以分成N/x,每组x人。每组的比较次数为x（x-1）/2，f[N]为最后决出冠军所需的比较次数，可以通过改变x的值使f[N]改变。题目给出t,l,r(1 ≤ t < 109 + 7, 2 ≤ l ≤ r ≤ 5·106)。求 t^0⋅f(l)+t^1⋅f(l+1)+⋯+t^r−l⋅f(r) 的最小值对1e9+7的模。
解题思路：
要解决题目的那条算式首先需要解决 f ( N ) 这个问题。
f (N) = (N/x) * x*(x-1)/2；
怎样使得 f(N) 尽可能小呢，模拟几个栗子会发现，分组越多比较的次数越少。比如6可以分为3个2或者2个3，所需比较数分别是6和7，8可以分为2个4 或 4个2，分别是 13、10；
所以尽量分下去，直到分到素数 x 为 1，f(N) = N*(N-1)/2;
综上所述（递推方法）：
①如果人数为素数，那f[N]=N(N-1)/2;
②如果不是素数，那就找出最小素因子x,分成N/x，每组x人，f[N]=N/x*f[x]+f[N/x]。
官方题解（内附 x 要为素数的证明，不过方法是dp）：
Suppose we have already calculated f(2), f(3), ..., f(r). Then calculating the value of the expression is easy.
Consider process of calculating f(x). Suppose we found optimal answer. Represent this answer as sequence of integers d1, d2, ..., dk — on the first stage we will divide girls into groups of d1 participants, on the second stage into groups of d2 participants and so on. Let us prove that all di should be prime.
Suppose some di is a composite number. Then it can be decomposed into two numbers di = a·b. In addition, let n girls are admitted to the i-th stage. Then on current i-th stage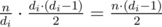 
comparisons will occur. But if we divide this stage into two new stages, then number of comparisons is 
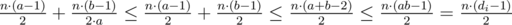. So, we proved that all di should be prime. Then it's easy to write DP which will be calculated by transition from the state to the states given by dividing current state by prime divisors. For solving this task we can use Eratosthenes sieve.
Total complexity is same as complexity of Eratosthenes sieve: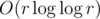 
.
In addition you can prove the fact that we should split the girls into groups by prime numbers in the order of their increasing. This optimization significantly accelerates the algorithm.
AC code:
1 #include <cstdio> 2 #include <iostream> 3 #include <algorithm> 4 #include <cstring> 5 #define LL long long 6 using namespace std; 7 const int MAXN = 5e6+10; 8 const LL mod = 1e9+7; 9 10 bool check[MAXN]; 11 LL prime[MAXN]; 12 LL f[MAXN]; 13 int cnt; 14 /* 15 void check_prime() //线性筛求素数 16 { 17 cnt = 0; 18 memset(check, false, sizeof(check)); 19 for(LL i = 2; i <= MAXN; i++){ 20 if(!check[i]) prime[++cnt] = i; 21 for(int k = 1; k <= cnt; k++){ 22 if(i*prime[k] > MAXN) break; 23 check[i*prime[k]] = true; 24 if(i%prime[k]) break; 25 } 26 } 27 } 28 */ 29 30 void check_prime(){ 31 memset(check, false, sizeof(check)); 32 for(int i=2;i*i<=MAXN;i++){ 33 if(!check[i]){ 34 prime[cnt++]=i; 35 for(int j=i*i;j<=MAXN;j+=i){ 36 check[j]=true; 37 } 38 } 39 } 40 } 41 42 int main() 43 { 44 check_prime(); 45 46 f[1] = 0; 47 for(LL i = 2; i < MAXN; i++){ 48 if(!check[i]){ 49 f[i] = (i*(i-1)/2)%mod; 50 } 51 else{ 52 LL fac; 53 for(int k = 0; k < cnt; k++){ 54 if(i%prime[k] == 0){ 55 fac = prime[k]; 56 break; 57 } 58 } 59 f[i] = (i/fac * f[fac] + f[i/fac])%mod; 60 } 61 } 62 63 LL T, l, r; 64 scanf("%I64d", &T); 65 scanf("%I64d %I64d", &l, &r); 66 LL ans = 0; 67 for(LL i = r; i >= l; i--){ 68 ans = (ans*T)%mod; 69 ans = (ans + f[i])%mod; 70 } 71 printf("%I64d ", ans); 72 return 0; 73 }
学习：
http://codeforces.com/blog/entry/53068?locale=en
https://www.cnblogs.com/fu3638/p/7115096.html
最后留个坑：
线性筛法O(N)求素数过不了，但是用Eratosthenes sieve.O(NlogN)可以。