任意门:https://nanti.jisuanke.com/t/31459
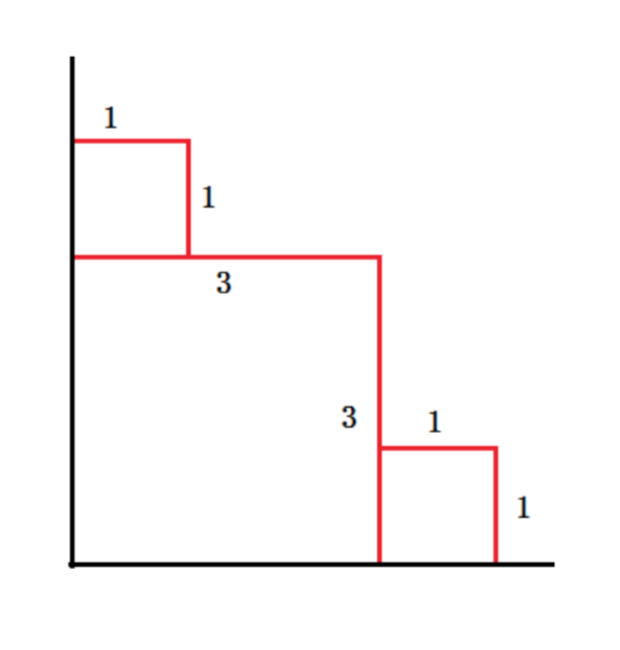
There's a beach in the first quadrant. And from time to time, there are sea waves. A wave ( xx , yy ) means the wave is a rectangle whose vertexes are ( 00 , 00 ), ( xx , 00 ), ( 00 , yy ), ( xx , yy ). Every time the wave will wash out the trace of former wave in its range and remain its own trace of ( xx , 00 ) -> ( xx , yy ) and ( 00 , yy ) -> ( xx , yy ). Now the toad on the coast wants to know the total length of trace on the coast after n waves. It's guaranteed that a wave will not cover the other completely.
Input
The first line is the number of waves n(n le 50000)n(n≤50000).
The next nn lines,each contains two numbers xx yy ,( 0 < x0<x , y le 10000000y≤10000000 ),the ii-th line means the ii-th second there comes a wave of ( xx , yy ), it's guaranteed that when 1 le i1≤i , j le nj≤n ,x_i le x_jxi≤xj and y_i le y_jyi≤yj don't set up at the same time.
Output
An Integer stands for the answer.
Hint:
As for the sample input, the answer is 3+3+1+1+1+1=103+3+1+1+1+1=10
样例输入
3 1 4 4 1 3 3
样例输出
10
题意概括:
有 N 个矩形海浪(给出右上角坐标), 后一个海浪会覆盖前一个海浪,求可见的海浪轮廓长度和。
解题思路:
按照从后往前遍历海浪(因为后面的会把前面的海浪覆盖),每次当前海浪的坐标分别减去当前海浪区间的最大值(x轴记录y的最大值, y值记录x的最大值)。
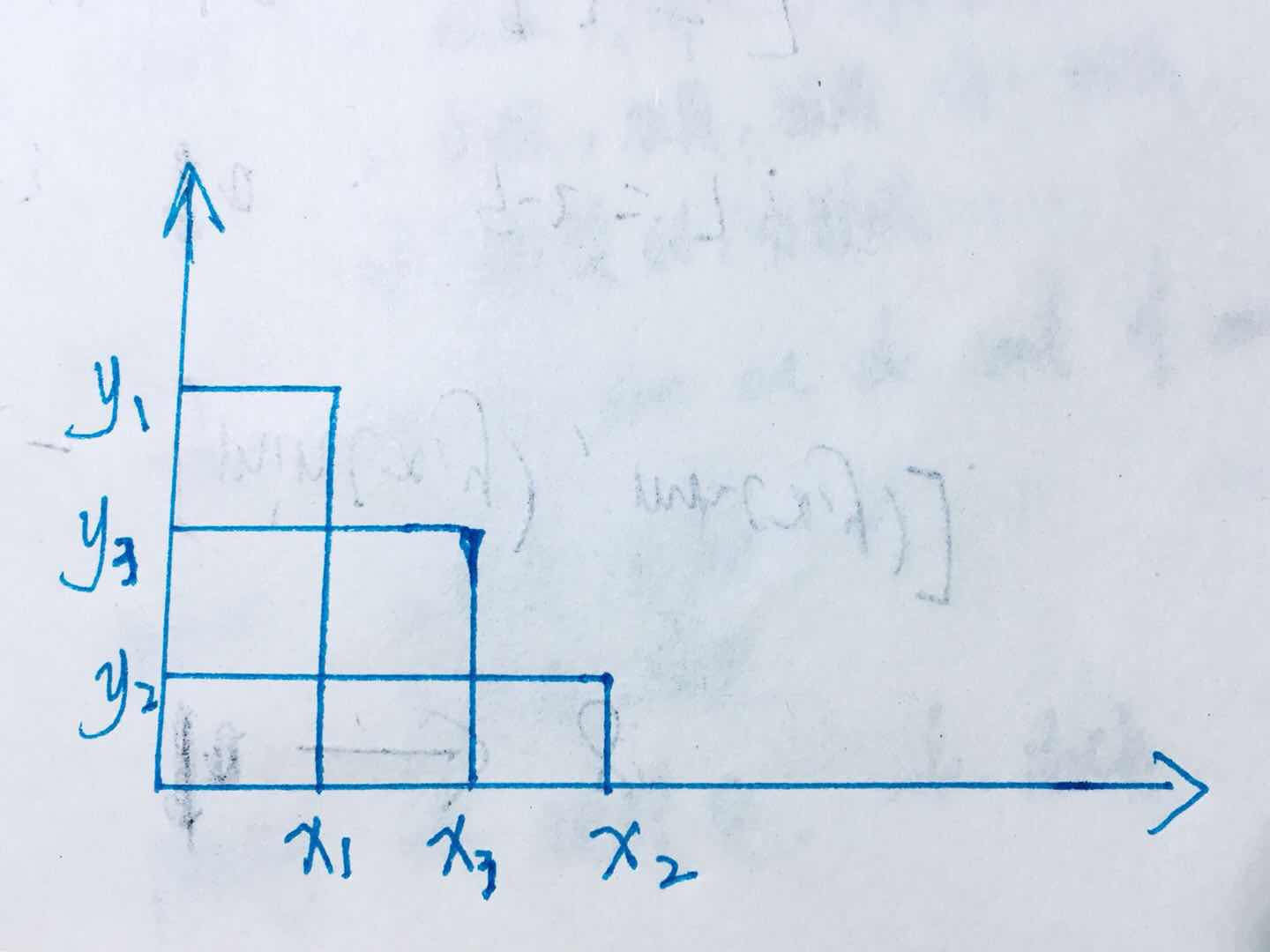
举个上面的栗子:
注意顺序是从后往前扫。
所以第一个是 x3,y3
0~x3 最大的 y 是 0 所以 第一条可见轮廓为 y3 - 0;
0~y3 的最大 x 是 0 所以 第二条可见轮廓为 x3 - 0;
分别更新这两段的最大值(用两个树状数组维护即可, 只更新【0, X】 和 【0,Y】这两个区间!!!)
第二个是 x2, y3
0 ~ x2 最大的 y 是 0 !!!(因为前面只更新到 x3) 所以第三条可见轮廓为 y2 - 0;
0 ~ y2 最大的 x 是 x3 所以第四条可见轮廓为 x2 - x3;
更新区间;
第三个是 x1 y1
0~x1 最大的 y3 是 0 所以 第五条可见轮廓为 y1 - y3;
0~y1 的最大 x3 是 所以 第六条可见轮廓为 x1 - x3;
更新区间;
AC code:

1 #include <bits/stdc++.h> 2 #define INF 0x3f3f3f3f 3 #define LL long long 4 using namespace std; 5 const int MAXN = 5e4+10; 6 7 LL res_x, res_y, ans; 8 LL t[MAXN*200]; 9 LL y[MAXN*200]; 10 int N; 11 12 struct date 13 { 14 LL x, y; 15 }wape[MAXN]; 16 LL lowbit(LL x) 17 { 18 return x&(-x); 19 } 20 21 void add(LL x ,LL val, int no) 22 { 23 for(LL i = x; i > 0; i-=lowbit(i)){ 24 if(no == 1) t[i] = max(t[i], val); 25 else y[i] = max(y[i], val); 26 } 27 } 28 29 LL query(LL x, int no) 30 { 31 LL res = 0; 32 for(LL i = x; i < MAXN*200; i+=lowbit(i)){ 33 if(no == 1) res = max(res, t[i]); 34 else res = max(res, y[i]); 35 } 36 return res; 37 } 38 39 int main() 40 { 41 scanf("%d", &N); 42 for(int i = 1; i <= N; i++){ 43 scanf("%lld%lld", &wape[i].x, &wape[i].y); 44 } 45 for(int i = N; i > 0; i--){ 46 res_y = wape[i].y - query(wape[i].x, 1); 47 if(res_y > 0) ans+=res_y; 48 res_x = wape[i].x - query(wape[i].y, 2); 49 if(res_x > 0) ans+=res_x; 50 51 add(wape[i].x, wape[i].y, 1); 52 add(wape[i].y, wape[i].x, 2); 53 } 54 printf("%lld ", ans); 55 return 0; 56 }