传送门:http://codeforces.com/contest/1087/problem/C
C. Connect Three
The Squareland national forest is divided into equal 1×11×1 square plots aligned with north-south and east-west directions. Each plot can be uniquely described by integer Cartesian coordinates (x,y)(x,y) of its south-west corner.
Three friends, Alice, Bob, and Charlie are going to buy three distinct plots of land A,B,CA,B,C in the forest. Initially, all plots in the forest (including the plots A,B,CA,B,C) are covered by trees. The friends want to visit each other, so they want to clean some of the plots from trees. After cleaning, one should be able to reach any of the plots A,B,CA,B,C from any other one of those by moving through adjacent cleared plots. Two plots are adjacent if they share a side.
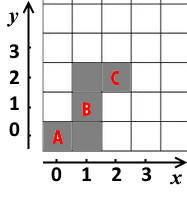 For example, A=(0,0)A=(0,0), B=(1,1)B=(1,1), C=(2,2)C=(2,2). The minimal number of plots to be cleared is 55. One of the ways to do it is shown with the gray color.
For example, A=(0,0)A=(0,0), B=(1,1)B=(1,1), C=(2,2)C=(2,2). The minimal number of plots to be cleared is 55. One of the ways to do it is shown with the gray color.Of course, the friends don't want to strain too much. Help them find out the smallest number of plots they need to clean from trees.
The first line contains two integers xAxA and yAyA — coordinates of the plot AA (0≤xA,yA≤10000≤xA,yA≤1000). The following two lines describe coordinates (xB,yB)(xB,yB) and (xC,yC)(xC,yC) of plots BB and CC respectively in the same format (0≤xB,yB,xC,yC≤10000≤xB,yB,xC,yC≤1000). It is guaranteed that all three plots are distinct.
On the first line print a single integer kk — the smallest number of plots needed to be cleaned from trees. The following kk lines should contain coordinates of all plots needed to be cleaned. All kk plots should be distinct. You can output the plots in any order.
If there are multiple solutions, print any of them.
0 0 1 1 2 2
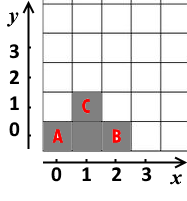
5 0 0 1 0 1 1 1 2 2 2
0 0 2 0 1 1
4 0 0 1 0 1 1 2 0
The first example is shown on the picture in the legend.
The second example is illustrated with the following image:
题意概括:
给三个格子的坐标,要求用最少的格子把这三个格子连起来,要求相邻格子相连需要是要有公共边。
解题思路:
所需要的总步数就是 X轴方向最大差值 加 Y轴方向最大差值 加 1.
输出的方格:
先按 X 小 Y 大的优先顺序对三个坐标排序。
从第一个点出发到第二个点,采取先沿着 X 轴 方向走,后沿着 Y轴 方向走,同时记录离第三个点的曼哈顿距离最近的一个转折点。
从转折点走到第三个点,采取先沿着Y轴方向走,后沿着 X轴方向走。
tip:如果担心会走重复的格子,加个标记就可以了。
AC code:
1 #include <queue> 2 #include <cmath> 3 #include <cstdio> 4 #include <vector> 5 #include <cstring> 6 #include <iostream> 7 #include <algorithm> 8 #define LL long long 9 using namespace std; 10 11 const int INF = 0x3f3f3f3f; 12 const int MAXN = 1e3+10; 13 int N; 14 15 struct date 16 { 17 int x, y; 18 }index[4]; 19 20 bool cmp(date a, date b) 21 { 22 if(a.x != b.x) return a.x < b.x; 23 else return a.y > b.y; 24 } 25 26 bool mmp[MAXN][MAXN]; 27 28 int main() 29 { 30 date kk, nxt; 31 int maxx = 0, maxy = 0, minx = INF, miny = INF; 32 for(int i = 1; i <= 3; i++){ 33 scanf("%d %d", &index[i].x, &index[i].y); 34 maxx = max(maxx, index[i].x); 35 maxy = max(maxy, index[i].y); 36 minx = min(minx, index[i].x); 37 miny = min(miny, index[i].y); 38 } 39 sort(index+1, index+4, cmp); 40 memset(mmp, 1, sizeof(mmp)); 41 int ans = (maxx-minx)+(maxy-miny)+1; 42 printf("%d ", ans); 43 printf("%d %d ", index[1].x, index[1].y); 44 kk.x = index[1].x; 45 kk.y = index[1].y; 46 nxt.x = index[2].x; 47 nxt.y = index[2].y; 48 mmp[kk.x][kk.y] = false; 49 50 int len = abs(index[2].x - index[1].x); 51 for(int i = 1; i <= len; i++){ 52 kk.x++; 53 if(mmp[kk.x][kk.y]) printf("%d %d ", kk.x, kk.y); 54 if(kk.x == index[3].x){ 55 nxt.x = kk.x; 56 nxt.y = kk.y; 57 } 58 mmp[kk.x][kk.y] = false; 59 } 60 61 len = abs(index[1].y - index[2].y); 62 for(int i = 1; i <= len; i++){ 63 if(index[1].y < index[2].y) kk.y++; 64 else kk.y--; 65 if(mmp[kk.x][kk.y]) printf("%d %d ", kk.x, kk.y); 66 if(kk.y == index[3].y){ 67 nxt.x = kk.x; 68 nxt.y = kk.y; 69 } 70 mmp[kk.x][kk.y] = false; 71 } 72 73 // printf("nxtx:%d nxty:%d ", nxt.x, nxt.y); 74 75 len = abs(index[3].y - nxt.y); 76 for(int i = 1; i <= len; i++){ 77 if(nxt.y < index[3].y) nxt.y++; 78 else nxt.y--; 79 if(mmp[nxt.x][nxt.y]) printf("%d %d ", nxt.x, nxt.y); 80 mmp[nxt.x][nxt.y] = false; 81 } 82 83 len = abs(index[3].x - nxt.x); 84 for(int i = 1; i <= len; i++){ 85 nxt.x++; 86 if(mmp[nxt.x][nxt.y]) printf("%d %d ", nxt.x, nxt.y); 87 mmp[nxt.x][nxt.y] = false; 88 } 89 90 return 0; 91 }