leetcode 118. Pascal's Triangle 、119. Pascal's Triangle II 、120. Triangle

118. Pascal's Triangle

第一种解法：比较麻烦

https://leetcode.com/problems/pascals-triangle/discuss/166279/cpp-beats-1002018.9.3(with-annotation) 

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> result;
        vector<int> res;
        for(int i = 1;i <= numRows;i++){
            for(int j = 1;j <= i;j++)
                res.push_back(1);
            result.push_back(res);
            res.clear();
        }
        if(numRows <= 2)
            return result;
        for(int i = 2;i < numRows;i++){
            for(int j = 1;j < i;j++){
                result[i][j] = result[i-1][j-1] + result[i-1][j];
            }
        }
        return result;
    }
};

第二种解法：

http://www.cnblogs.com/grandyang/p/4032449.html

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> result(numRows,vector<int>(numRows,1));
        for(int i = 0;i < numRows;i++){
            result[i].resize(i+1);
            for(int j = 1;j <= i-1;j++){
                result[i][j] = result[i-1][j-1] + result[i-1][j];
            }
        }
        return result;
    }
};

119. Pascal's Triangle II

这个题与118. Pascal's Triangle不同的是只求这一行的数值，并且输入的是下标index，不是n，即index = n-1。

这个题要实现O(k) 的空间复杂度，那申请存储的大小就只能是k个大小，即那行所具有的元素的个数。

每个数值来自于上一行同列的数值+上一行小一列的数值。

当前这个一维数组存储的值，其实是上一行同列的值，所以只需要再加上小一列的数值即可以。

注意：这里只能从每行的右侧向左侧进行计算，不能从左侧向右侧进行计算，只有从右侧向左侧计算，当前位置存储的原始值才能代表上一行同列的值。

从右向左的原因是当前位置的值是上一行当前位置和上一行前一个位置的值的和，所以前一个要在后一个位置之后发生变化

类似如下图：

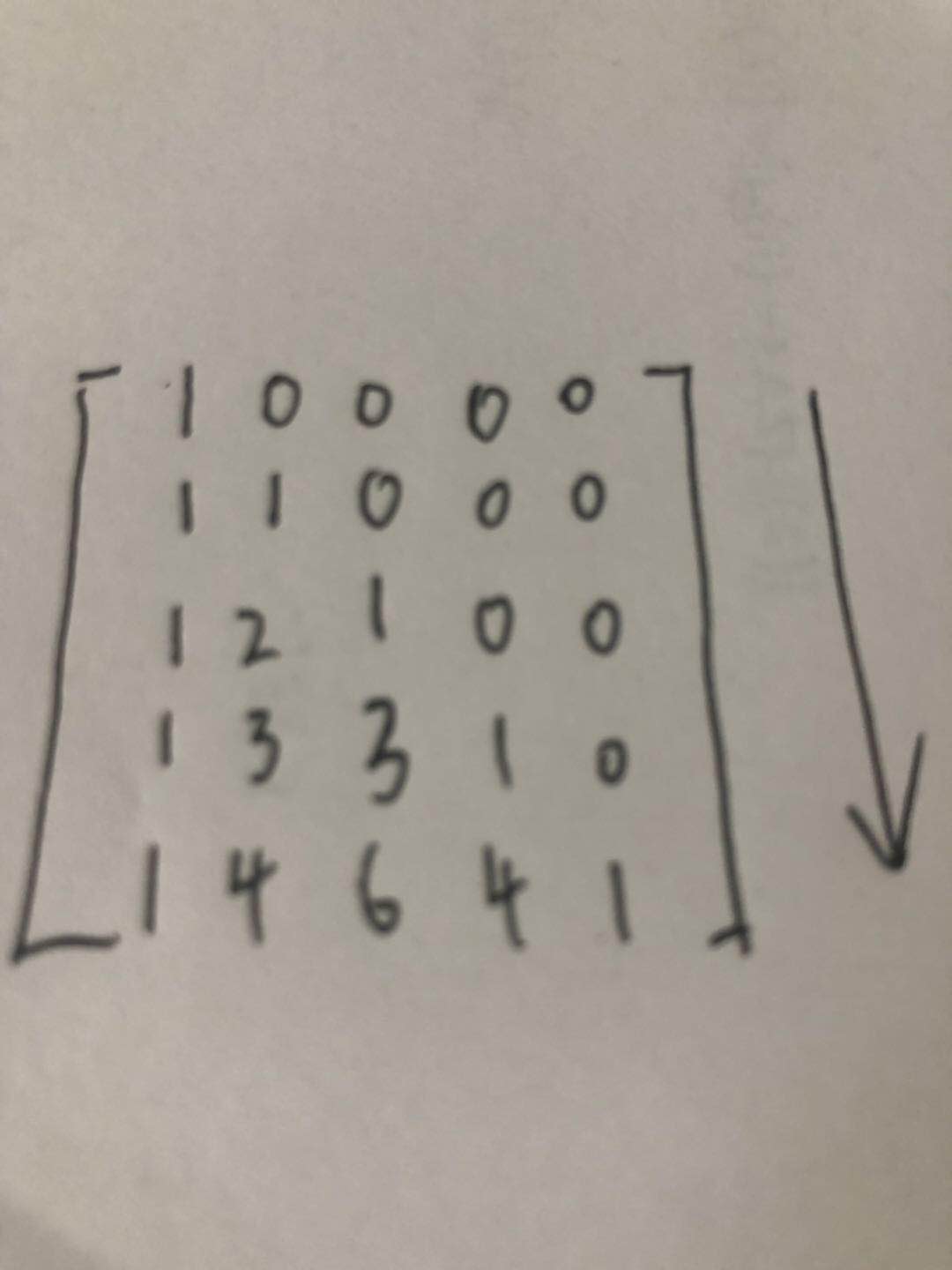
实质上就是每次增加一行，增加了一列，所有0之前的数字都对应保存着上一行同样列的值

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> res(rowIndex + 1,0);
        res[0] = 1;
        for(int i = 1;i <= rowIndex;i++){
            for(int j = i;j > 0;j--){
                res[j] += res[j-1];
            }
        }
        return res;
    }
};

120. Triangle

https://www.cnblogs.com/grandyang/p/4286274.html

暴力的方式是将所有路径搜索一遍，这样的时间复杂度是n！。

方法一是使用动态规划的方法，当前值只可能来自同行同列和同行少一列。

方法一：

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int height = triangle.size();
        if(height <= 0)
            return 0;
        if(height == 1)
            return triangle[0][0];
        int width = triangle[height-1].size();
        vector<vector<int>> result(height,vector<int>(width));
        result[0][0] = triangle[0][0];
        for(int i = 1;i < height;i++){
            width = triangle[i].size();
            for(int j = 0;j < width;j++){
                if(j !=0 && j != (width-1)){
                    result[i][j] = min(result[i-1][j] + triangle[i][j],result[i-1][j-1] + triangle[i][j]);
                }
                else if(j == 0)
                    result[i][j] = result[i-1][j] + triangle[i][j];
                else
                    result[i][j] = result[i-1][j-1] + triangle[i][j];
            }
        }
        int min_num = 0x7fffffff;
        for(int i = 0;i < triangle[height-1].size();i++){
            if(min_num > result[height-1][i])
                min_num = result[height-1][i];
        }
        return min_num;
    }
};

方法二：

此方法将空间复杂度优化到O(n)。类似Pascal's Triangle II用一个一维数组进行计算，但此题是从最后一行出发进行遍历。

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) {
        int m = triangle.size();
        if(m <= 0)
            return 0;
        vector<int> dp = triangle[m-1];
        for(int i = m-2;i >=0;i--){
            for(int j = 0;j <= i;j++){
                dp[j] = min(dp[j],dp[j+1]) + triangle[i][j];
            }
        }
        return dp[0];
    }
};