leetcode 67. Add Binary 、2. Add Two Numbers 、445. Add Two Numbers II 、43. Multiply Strings 字符串相乘 、29. Divide Two Integers

对于几进制，其实主要就是对进制取余和整除，取余的结果就是当前位的，整除的结果就是进位的。

67. Add Binary

https://www.cnblogs.com/grandyang/p/4084971.html

从两个string的末尾开始转int型相加，注意carry的计算。

如果某一个数少于另一个数，就用0代替这一位，这种思路记住：

int num1 = m >= 0 ? (a[m--] - '0') : 0;
int num2 = n >= 0 ? (b[n--] - '0') : 0;

class Solution {
public:
    string addBinary(string a, string b) {
        int m = a.size(),n = b.size();
        if(m <= 0)
            return b;
        if(n <= 0)
            return a;
        m--,n--;
        string res = "";
        int carry = 0;
        while(m >= 0 || n >= 0){
            int num1 = m >= 0 ? (a[m--] - '0') : 0;
            int num2 = n >= 0 ? (b[n--] - '0') : 0;
            int sum = num1 + num2 + carry;
            carry = sum/2;
            res = to_string(sum % 2) + res;
        }
        return carry == 0 ? res : "1" + res;
    }
};

2. Add Two Numbers

这题的解题思路几乎与Add Binary一模一样，变化在于每次要生成一个新的链表，然后用当前的尾节点指向。注意if(p1)和if(p2)的使用。

http://www.cnblogs.com/grandyang/p/4129891.html

依旧记住ListNode* p1 = l1,p2 = l2;这样写是会报错的，int、float这样初始化都没有问题。

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        if(l1 == NULL)
            return l2;
        if(l2 == NULL)
            return l1;
        ListNode* p1 = l1;
        ListNode* p2 = l2;
        ListNode* dummy = new ListNode(-1);
        ListNode* cur = dummy;
        int carry = 0;
        while(p1 != NULL || p2 != NULL){
            int num1 = p1 == NULL ? 0 : p1->val;
            int num2 = p2 == NULL ? 0 : p2->val;
            int sum = num1 + num2 + carry;
            carry = sum/10;
            int value = sum%10;
            cur->next = new ListNode(value);
            cur = cur->next;
            if(p1)
                p1 = p1->next;
            if(p2)
                p2 = p2->next;
        }
        if(carry)
            cur->next = new ListNode(carry);
        return dummy->next;
    }
};

445. Add Two Numbers II 

这个题和Add Two Numbers相似，但是这个题是把最高位放在了链表的前面，但数字的相加必须从最低位开始。

可以选择用栈来存储数字，也可以使用链表反转。

使用链表反转，先将l1、l2反转，然后时候用和Add Two Numbers一样的方法做计算，然后再反转这个生成的记过就好了。

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        if(l1 == NULL)
            return l2;
        if(l2 == NULL)
            return l1;
        l1 = reverse(l1);
        l2 = reverse(l2);
        ListNode* p1 = l1;
        ListNode* p2 = l2;
        ListNode* dummy = new ListNode(-1);
        ListNode* cur = dummy;
        int carry = 0;
        while(l1 != NULL || l2 != NULL){
            int num1 = l1 == NULL ? 0 : l1->val;
            int num2 = l2 == NULL ? 0 : l2->val;
            int sum = num1 + num2 + carry;
            carry = sum/10;
            cur->next = new ListNode(sum%10);
            cur = cur->next;
            if(l1)
                l1 = l1->next;
            if(l2)
                l2 = l2->next;
        }
        if(carry)
            cur->next = new ListNode(carry);
        ListNode* res = reverse(dummy->next);
        return res;
    }
    ListNode* reverse(ListNode* node){
        ListNode* pre = NULL;
        ListNode* cur = node;
        while(cur){
            ListNode* tmp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
};

43. Multiply Strings

https://www.cnblogs.com/grandyang/p/4395356.html

将问题转换为正常的数字相乘计算过程。

m位数字和n位数字相乘，生成的数字最多只有m+n位。

从低位相乘到高位，每次取出的两个数的乘积要加上之前一个低位保存的数字，低位更新保存的数字，高位加上进位的数字。result[i+j+1] = sum%10只能是等于符号，不能是加号。因为你需要更新低位的数字。

在生成的数字中可能在低位存在多个0，这个时候都需要跳过不转换为string。

Input:
"9133"
"0"
Output:
"0000"

class Solution {
public:
    string multiply(string num1, string num2) {
        int m = num1.size(),n = num2.size();
        vector<int> result(m+n,0);
        string res = "";
        for(int i = m - 1;i >= 0;i--){
            for(int j = n - 1;j >= 0;j--){
                int sum = result[i+j+1] + (num1[i] - '0') * (num2[j] - '0');
                result[i+j+1] = sum%10;
                result[i+j] += sum/10;
            }
        }
        for(int i = 0;i < result.size();i++){
            if(res.empty() && result[i] == 0)
                continue; 
            res += result[i] + '0';
        }
        return res.empty() ? "0" : res;
    }
};

29. Divide Two Integers

这道题让我们求两数相除，而且规定我们不能用乘法，除法和取余操作，所以本题使用位操作。

在这里核心思路是使用逆向二分法的思路来进行计算。

既然不能用乘、除、取模，只能用移位操作来完成了。将除数 divisor 每次左移一位，找到最接近被除数且不大于被除数 dividend的一个数，然后将被除数减去这个数，继续之前的操作。例如：31除以3，将3不断左移，直到左移3位后达到最接近31且不大于31的数，即3*2*2*2=24(此时相当于将3乘以了8，这个8是结果的一部分)，然后将31-24=7，继续之前的操作，左移3，直到最接近7且不大于7的一个数，即将3左移一位得到3*2=6（这个2也是结果的一部分），然后7-6=1，继续之前的操作，因为3已经大于1了，所以不需要左移了，即得到最后的结果为：8+2=10

https://blog.csdn.net/xiaoguaihai/article/details/84594248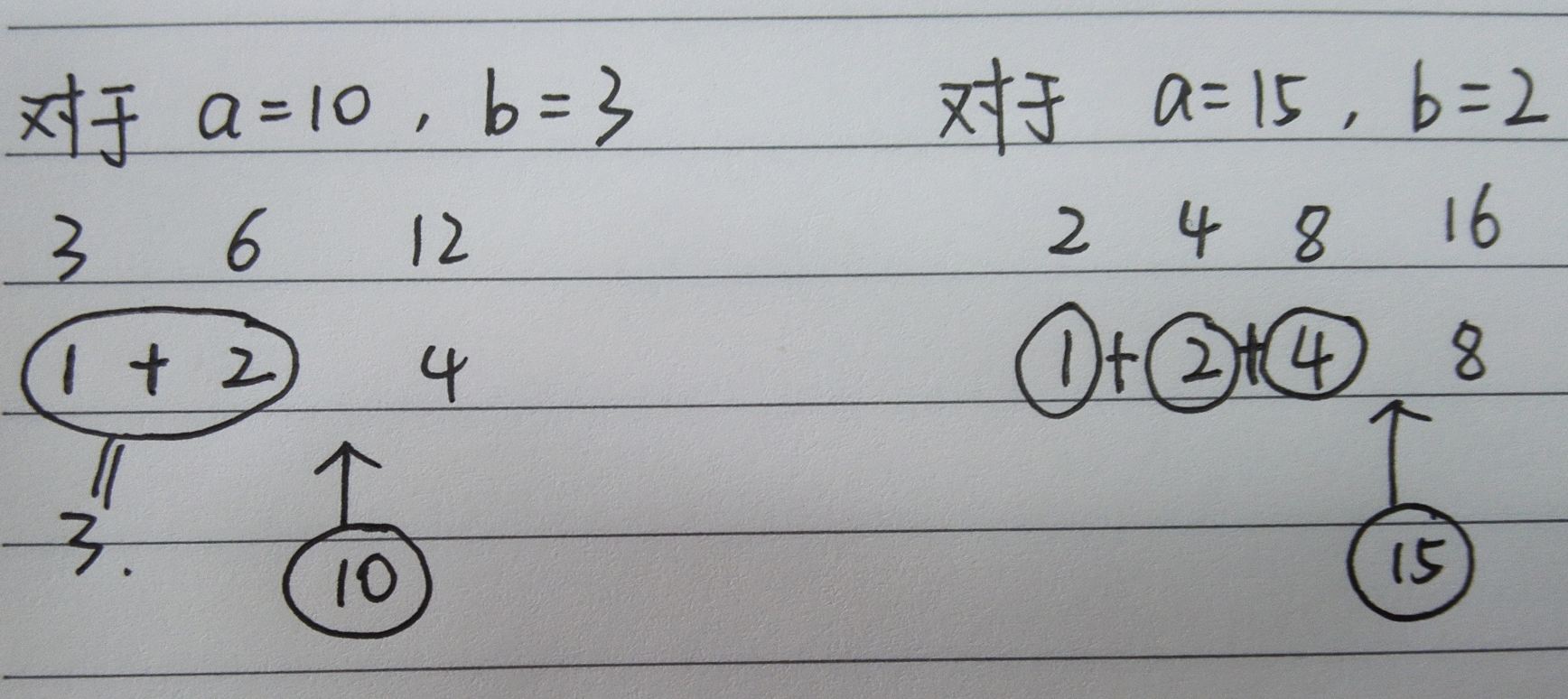 

oj上有个test case如下：

-2147483648
-1

必须用long long来计算才能不保证溢出。

freq必须初始化为1，不然左移乘以两倍也不发生变化。每次判断条件必须先判断乘以2倍后是否超过m，如果不超过，就不用进行循环，freq也就不用再翻倍。

注意两个循环的判断条件都是大于等于>=，等于的情况也必须计算。

刚开始写了一个错误代码：

tmp << 1;
freq << 1;

这样会造成无限循环，因为tmp和freq的值并没有发生变化，我以为左移了就自动发生变化了，还是需要赋值的。

class Solution {
public:
    int divide(int dividend, int divisor) {
        long long res = 0;
        long long m = abs((long long)dividend),n = abs((long long)divisor);
        while(m >= n){
            long long tmp = n;
            long long freq = 1;
            while(m >= (tmp << 1)){
                tmp = tmp << 1;
                freq = freq << 1;
            }
            m = m - tmp;
            res += freq;
        }
        if((dividend > 0) ^ (divisor > 0))
            res = -res;;
        return res > INT_MAX ? INT_MAX : res;
    }
};