聚类-均值漂移

一、算法简介

1. 均值漂移算法首先找到一个中心点center（随机选择），然后根据半径划分一个范围
2. 把这个范围内的点输入簇c的标记个数加1
3. 在这个范围内，计算其它点到这个点的平均距离，并把这个平均距离当成偏移量 shift
4. 把中心点center移动偏移量 shift 个单位，当成新的中心点
5. 重复上述步骤直到 shift小于一定阈值，即收敛
6. 如果当前簇c的center和另一个簇c2的center距离小于一定阈值，则把当前簇归类为c2，否则聚类的类别+1
7. 重复1、2、3、4、5、6直到所有点都遍历过
8. 如果一个点既被簇c1遍历过，也被簇c2遍历过，则把其归类为标记数多的簇

根据上述描述均值漂移聚类也就是根据密度来聚类的，样本会属于密度最大的那个类别的簇

二、一些计算

 1、基础偏移量

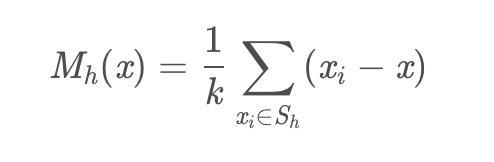
• S_h为球半径内的点集合
• 也就是用集合内的点与质心相减得到累计的偏移量

2、高斯偏移量

• 在基础偏移量计算中，集合范围内距离簇心越远的点拥有越大的权重，这不合理
• 距离簇心越近的点应该跟簇心的类别越接近，因此此类的点应该有更大的权重

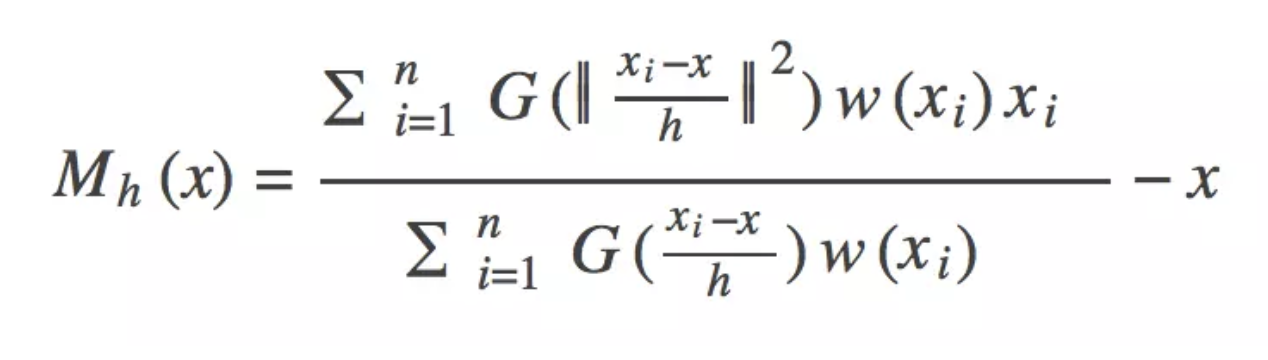
3、更新新的质心为

三、Code

from scipy.spatial import distance
from sklearn.neighbors import NearestNeighbors
from sklearn.cluster.dbscan_ import DBSCAN
from sklearn.cluster.dbscan_ import dbscan
import numpy as np
from matplotlib import pyplot as plt
from sklearn.cluster import MeanShift, estimate_bandwidth

from sklearn.cluster.tests.common import generate_clustered_data

min_samples = 10
eps = 0.0309

X = generate_clustered_data(seed=1, n_samples_per_cluster=1000)

#quantile 控制是否同一类别的距离
bandwidth = estimate_bandwidth(X, quantile=0.3, n_samples=len(X))
meanshift = MeanShift(bandwidth=bandwidth, bin_seeding=True)  # 构建对象
meanshift.fit(X)
labels = meanshift.labels_

print(np.unique(labels))

fig, ax = plt.subplots()
cluster_num = len(np.unique(labels))  # label的个数，即自动划分的族群的个数
for i in range(0, cluster_num):
    x = []
    y = []
    for ind, label in enumerate(labels):
        if label == i:
            x.append(X[ind][0])
            y.append(X[ind][1])
    ax.scatter(x, y, s=1)

plt.show()

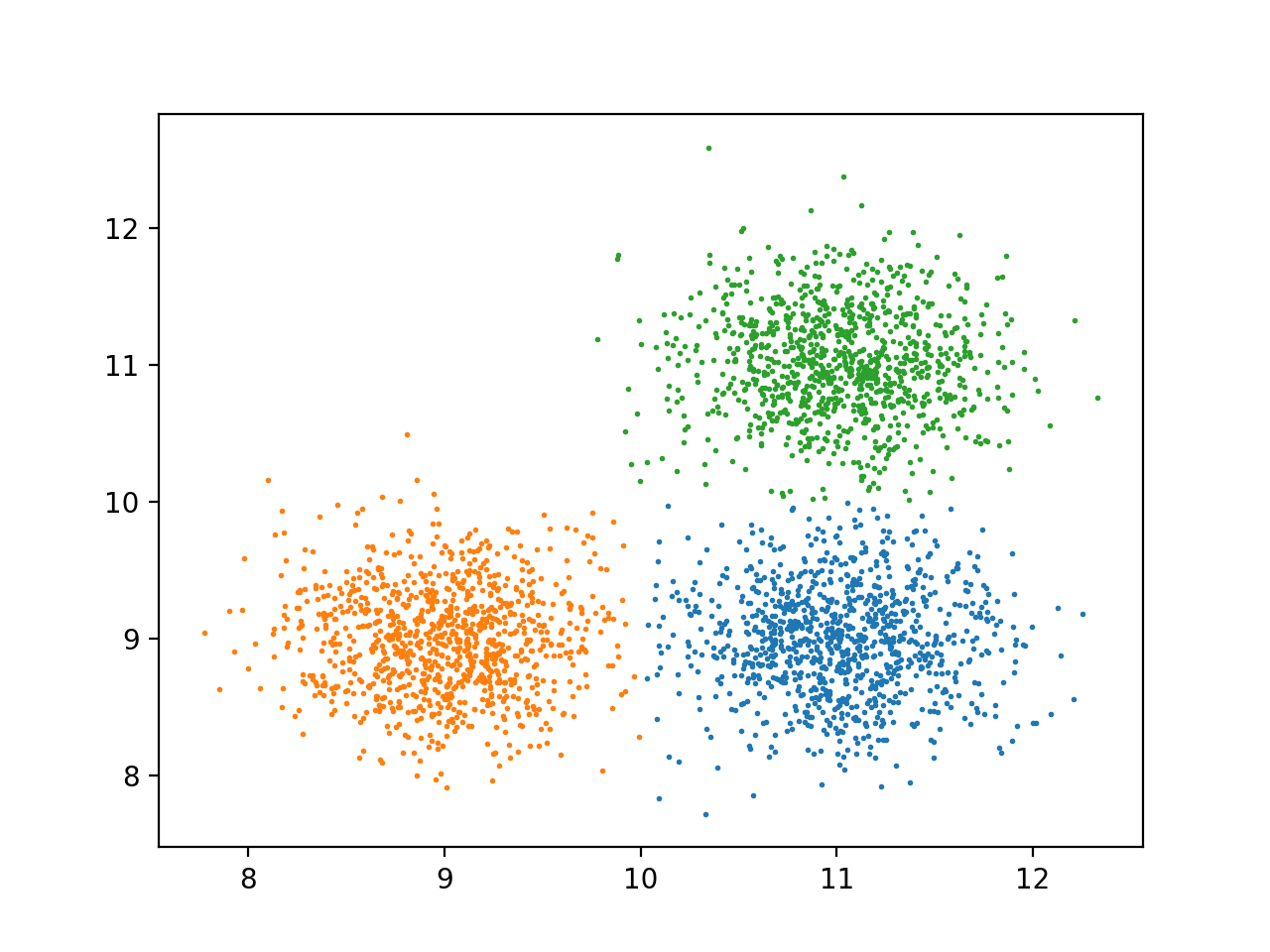
结果