一、定理大概描述
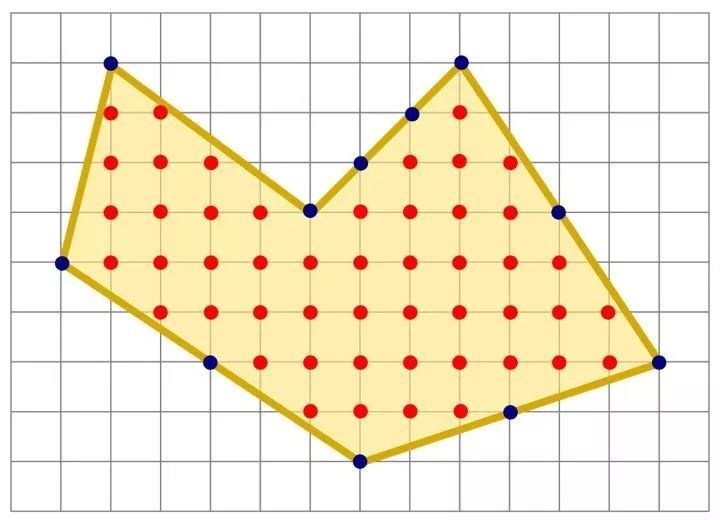
- 给定一个网格,每个格子由边长为1的单位正方形组成。
- 网格内有一个多边形,并且多边形的顶点都在网格的交点处,也就是说顶点没有一个落在了单位正方形的边上或者单位正方形的内部
- 记多边形的面积为S,多边形内部的点的个数为I,多边形边上的点数为A
- 则多边形的面积为 $$S=I+frac{A}{2}-1$$
二、证明
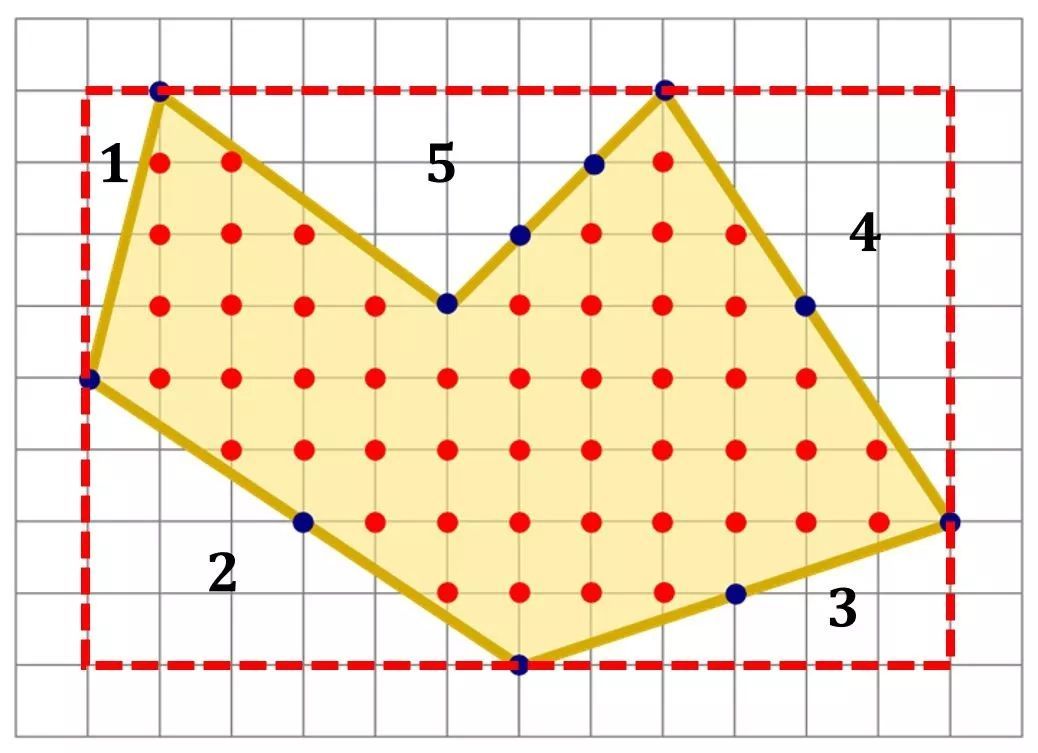
在这样的形状内
$$S_{polygon}=S_{rectangle}-sum S_{triangle}$$
区域5的三角形可以可以拆成两个直角三角形之和
1、证明步骤
- (1)首先,证明对长方形是成立的;
- (2)接着,再证明对直角三角形是成立的;
- (3)然后,继续证明对任意三角形也是成立的;
- (4)最后,证明对于两个图形的组合还是成立的。
首先证明(4)
- 假设任意一个多边形的面积都有$$S=I+frac{A}{2}-1$$,
- 则设定一个四边形为$T_{1}$,边上的点为 $A_{1}$, 内点$I_{1}$,
- 以$T_{1}$的一条边(顶点数目为n)为公共边生成另一个多边形$T_{2}$,边上的点为$A_{2}$, 内点为$I_{2}$
- 合成的多边形内点$I_{1} + I_{2} + n - 2$, 边上的点 $A_{1} + A_{2} - 2n + 2$
- 则$$I_{1} + I_{2} + n - 2 + frac{(A_{1} + A_{2} - 2n +2)}{2}-1 = I_{1}+ frac{A_{1}}{2} -1 + I_{2} - frac{A_{2}}{2} -1$$
因此此假设成立
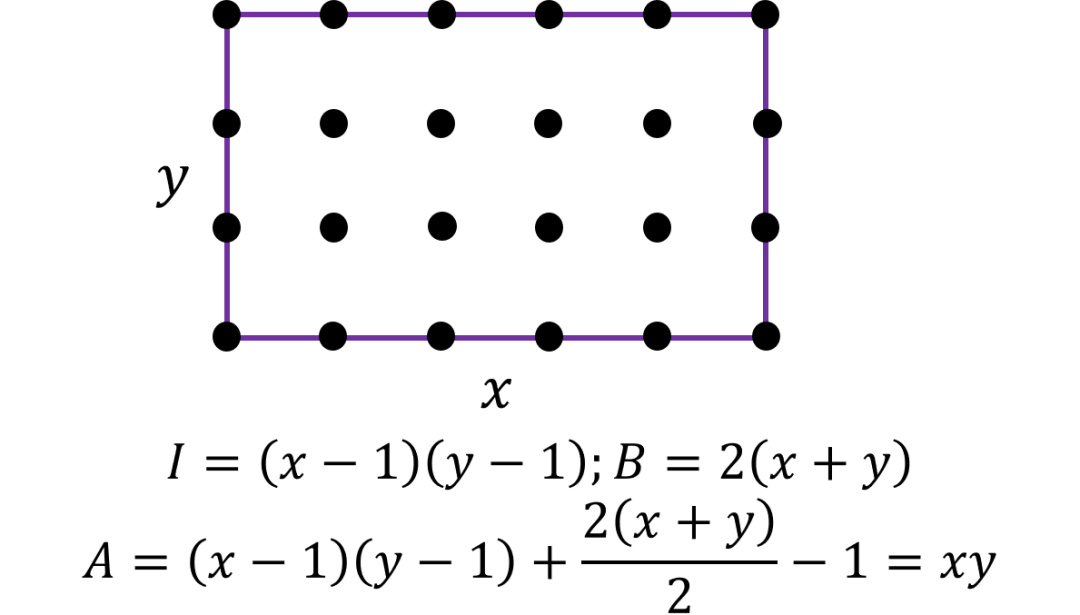
(1) 证明对长方形是成立的
长方形的长、宽长度分别为x,y
(2) 证明对于三角形是成立的
首先考虑直角三角形
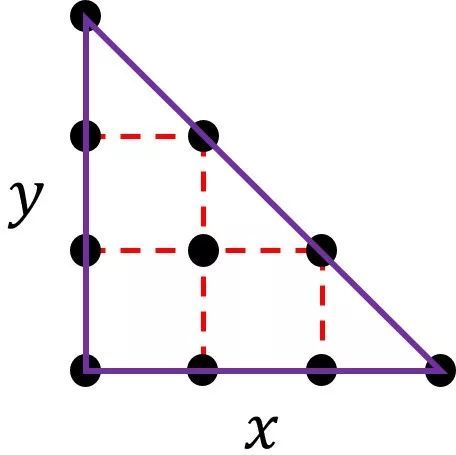
将其放入矩形中,则这个矩形是两个直角三角形的和。假设公共边,也就是矩形的对角线上的点为n,则
- $$S_{right\_triangle} = frac{xy}{2}$$
- $$A = x + y + n - 1, I =frac{(x-1)*(y-1 ) - (n-2)}{2}$$
- $$S = I + frac{A}{2} - 1 = frac{xy - x - y - n + 3}{2} + frac{x + y + n - 1}{2} - 1 = frac{xy}{2}$$
(3) 任意三角形
对于任意三角形可以由 1个长方形 = 若干直角三角形 + 此三角形 拼接而成,用上面拆解的方法同理可证

多边形可以由这些三角形、直角三角形、长方形拼接而成,由4的叠加性,证明完毕。