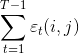摘自
1.李航的《统计学习方法》
2.http://www.cnblogs.com/pinard/p/6955871.html
一、概率计算问题
上一篇介绍了概率计算问题是给定了λ(A,B,π),计算一个观测序列O出现的概率,即求P(O|λ)。
用三种方法,直接计算法,前向算法,后向算法。
考虑隐马尔可夫模型(一)中的盒子球模型。
假设Q={1,2,3,4}, V = {红,白},在给定λ(A,B,π)的条件下,其中:
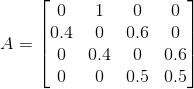 ,
, 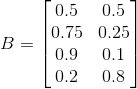 ,
,

求O=(红,白,红)的概率。
二、直接计算法
说通俗一点,就是暴力求解,穷举法。
- 所有可能的状态序列I,则状态序列I的概率为P(I|λ)
- 对于固定的状态序列I,则观测序列为O的概率P(O|I,λ)
- 联合概率为P(O,I|λ) = P(O|I,λ)P(I|λ)
- 则最后所求为P(O|λ) = ΣP(O|I,λ)P(I|λ)
状态集合有N个,一共有T个状态序列,所以状态序列的可能性为NT,每一种状态序列都要相应乘以T个观测概率矩阵,所以最后的时间复杂度为O(TNT)。
三、前向计算法
记αi(j)为部分观测序列为o1.....ot切ot状态为qj的概率。
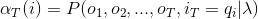
首先,记alphai(j)为第i次观测下状态为j,观测值为O(i)的概率,bj(i)为j状态下观测值为O(i)的概率, 暂时记i=1为红球,i=2为白球, aij为矩阵A中i行j列。
1、第一次观测为红球
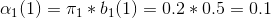


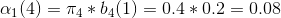
2、第二次观测为白球

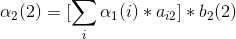
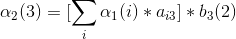
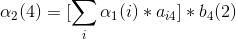
3、第三次观测
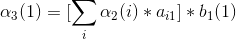
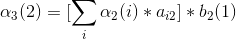
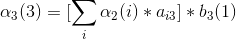
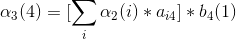
4、最后结果
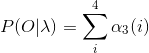
四、后向计算方法
βt(i)为On, On-1.... Ot观测序列且在Ot时刻状态为qi的概率:
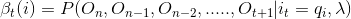
五、总结
根据前向传播算法,可以得到一些相关概率和期望。
1、给定模型输入λ和观测O,在时刻t处于状态qi 的概率为γt(i)。
(1)记γt(i):
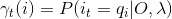
(2)由前向概率和后向概率表达式α和β可得:
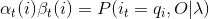
(3)因此:

(4)因此得到γt(i)
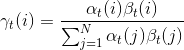
2、给定模型λ和观测O,在时刻t处于状态qi,且在时刻t+1处于状态qj的概率为εt(i, j)。
(1)记εt(i, j):
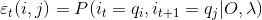
(2)通过前向后向计算可以得到:

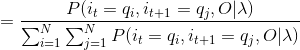
(3)由于:
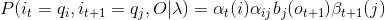
(4)因此:
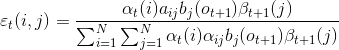
3、在观测O下由状态i出现的期望值:

4、在观测O下由状态i转移的期望值
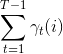
5、在观测O下由状态i转移到状态j的期望值: