0 引子
嗯,开始之前先介绍几个概念:
目标串:也就是主串,待匹配的串。
模式串:去匹配的串。
子串:原串中的某一连续片段。
前缀:原串前面连续部分组成。
后缀:原串尾部连续部分组成
其实,不用被这些术语搞晕,更不必记忆,转化为自己的东西,理解了就好。
抛个问题先:
现在有两个字符串,其中一个是模式串abcabcacab,另一个是目标串babcbabcabcaabcabcabcacabc,用什么方法能快速判断目标串中是否包含模式串。
学习是个循序渐进的过程,学习算法尤其如此,所以我们由经典算法开始,一步一步深入。
经典的算法思想就是挨个匹配,失配了就整体对齐到下一位继续匹配。
step1:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| b | a | b | c | b | a | b | c | a | b | c | a | b | c | a | a | b | c | a | b | c | a | c | a | b | c |
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| N |
第一位不匹配。
step2:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| b | a | b | c | b | a | b | c | a | b | c | a | b | c | a | a | b | c | a | b | c | a | c | a | b | c |
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| N |
第四位不匹配。
太多就不展开了,这样依次下去,最后肯定可以得出正确的结果。
哎,太容易想到的往往效率不高,经过上面的介绍,大家应该对这个问题有了自己的认识,我一直觉得,想要解决问题一定要对问题本身有深刻的认识,这也是我一直跟队友强调的。如果没有知其然,知其所以然的态度,建议不用继续看下去,毕竟下面要说的单模式匹配KMP算法和BM算法,都出来这么多年了,很多库都有封装,对于很多人来说真的是会用就行。
1 KMP算法
有时刷一些字符串相关的题时,经常会用到KMP算法,其实时间长了,自己也有点忘,就直接依靠以前的模板了,现在网络方便了,自己却变懒惰了,扪心自问:你能给一个完全没这方面基础的人,讲清楚什么是KMP算法吗?
KMP算法是三个人共同提出的,K,M,P分别是这三个人名字的首字母。KMP算法的主要思想是,利用模式串自身的信息,得到next表,next表主要用于失配时的跳跃。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| b | a | b | c | b | a | b | c | a | b | c | a | b | c | a | a | b | c | a | b | c | a | c | a | b | c |
| a | b | c | a | b | c | a | c | a | b | ||||||||||||||||
| Y | Y | Y | Y | Y | Y | Y | N |
上面是匹配过程中的一个状态,为了叙述方便,现在将模式串称P,目标串称为T,现在T[7] != P[12],观察下我们发现1. T[3~6] = P[8~11] 2. T[0~3] = T[3~6],发现这两点应该没什么难度。代换下,进一步发现T[0~3] = P[8~11],这样我们就不用像经典的算法那样,一次只跳一步,现在我们可以直接跳四步,直接去匹配第五位。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| b | a | b | c | b | a | b | c | a | b | c | a | b | c | a | a | b | c | a | b | c | a | c | a | b | c |
| a | b | c | a | b | c | a | c | a | b | a | |||||||||||||||
| ? |
根据上面的结论,前四位匹配肯定成功,直接从第五位开始比较。
通过上面的分析,我们尝到了KMP思想的甜头,一次跳跃了四位,避免了很多无效的比较。仔细的观察下,上面的做法其实只用到了模式串的特性,和目标串并没什么联系,如果我们提前得到一张模式串的next表,那么失配时,不是可以直接去查表然后计算如何跳跃吗?嗯,对!关键是怎么得到这张表。
得到next表前,我们先要得到这样一张表,前缀自包含的长度,还是举个例子吧,对于上面的模式串T,我们求T[5]的前缀自包含长度,abcabcacab主要就是求T[0~4]中T[0~x] = T[4-x~4]中x的值,显然这里的x=1,那么T[5]前缀自包含的长度就是2,移动的步数 = 已匹配的长度 - 前缀自包含长度 = 5 - 2 = 3。也就是说在T[5]处失配时,直接向前跳3步,因为已经匹配的长度等于5,即T[0~4],前缀自包含长度等于2。
KMP的精髓也就next表,而next表的核心是前缀自包含长度,现在大家应该比较清晰了,梳理下思路就可以自己写出来了。
比较晚了,下面的BM算法,AC算法,WM算法先欠着。 0. 0
2 BM算法
这货的效率平均比KMP高3~4倍(要知道,KMP已经是O(n)的!),平时编辑器里的ctrl+F,grep之类的都是使用的这个算法。但是这个算法的核心和KMP没什么大的区别,只是换了种方式,再加上了一些自己的规则。
BM算法在匹配中失配时,有两个核心的跳转规则1. 坏字符规则 2. 好后缀规则。BM算法匹配的顺序和KMP的匹配顺序刚好相反,BM是从后往前匹配的。
为了讲解方便还是举个例子,现在的模式串P是abcab,目标串T是aacadabaccabcab,在他们匹配的过程中来讲解什么是坏字符规则,什么是好后缀规则。
step1:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| a | a | c | a | d | a | b | a | c | c | a | b | c | a | b |
| a | b | c | a | b | ||||||||||
| N |
BM从后往前匹配,发现T[4] != P[4],同时T[4]这个字符在模式串中并没有出现过。在这里T[4]是一个坏字符,在模式串中没有字符能和其匹配,下一步可以整体跳到T[4]之后再匹配。
step2:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| a | a | c | a | d | a | b | a | c | c | a | b | c | a | b |
| a | b | c | a | b | ||||||||||
| N |
整体跳转后,还是按照前面的规则匹配最后一个字符,发现T[9] != P[4],此时模式串中是包含T[9]的。在这里T[9]也是一个坏字符,遇到这种情况就让T[9]依次和模式串中相同的字符对齐(按照从后往前的方式),模式串中只出现一次T[9]。
setp3:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| a | a | c | a | d | a | b | a | c | c | a | b | c | a | b |
| a | b | c | a | b | ||||||||||
| N | Y | Y | Y |
对齐T[9]后还是从后往前匹配,发现T[8] != P[1],但是我们发现1. T[10~11] = P[3~4] 2. P[3~4] = P[0~1],那么显然T[10~11] = P[0~1]。这里我们就要用到好后缀规则了,这次跳转可以直接让P[0]和T[10]对其。
step4:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| a | a | c | a | d | a | b | a | c | c | a | b | c | a | b |
| a | b | c | a | b | ||||||||||
| Y | Y | Y | Y | Y |
此时发现已经匹配成功。
我们一共用了四步就匹配成功了,可以看出BM算法的效率很高,现在我们清楚了BM算法是如何匹配的已经坏字符和好后缀规则了。规则多了,效率高了,但是重要的是要清楚这些规则如何使用,他们的优先级如何。
假设现在我们已经有了坏字符表(key:坏字符 value:移动步数)和好后缀表,当模式串和目标串失配时,分别去两张表查要跳转的步数然后选其中较大的跳转即可。
现在问题就变得很简单了,但是前提是你得到了这两张表。原理知道了,难点还是后面的好后缀表如果生成,如果上面的KMP看懂了,其实这也不是什么难事。
3 AC算法
还是抛个问题:
现在有一个文本T,有n个单词,现在让你找出有多少个单词在文本T中出现过?
如果n=1,那么问题就退化为上面的问题了。当然你也可以使用n次KMP或BM来解决这个问题,虽然这样很low。要想弄懂AC自动机,需要先搞清楚Trie树和KMP算法的思想。
嗯,KMP上面已经介绍了,来简单说说Trie树,Trie树也叫字典树,前缀树。Trie树是一种很好的结构,但是用处很大,插入查询的效率都是O(n),每一个公共前缀只用一个节点来保存,压缩了存储空间。
还是举个例子,现在我用she, shr,say, her,he5个单词来创建一颗Trie树。
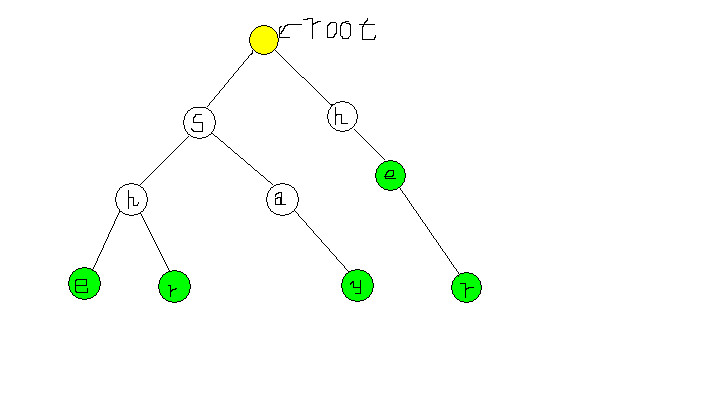
其中用绿色标出的点表示一个单词的末尾,观察下发现Trie树有如下特点:
1.构造一棵Trie,作为AC自动机的搜索数据结构。
2.构造fail指针(失配时的跳转指针,我们可以利用 bfs在 Trie上面进行 fail指针的求解。)
3.扫描主串进行匹配。
先解释先第一步和最后一步,第一步就是建树这都能理解按照规则建就好了,最后一步就是去匹配,当失配就跳转到fail指针所指的位置,然后继续匹配,匹配的过程中更新统计结果就行了。
最难的是如何构造fail指针,其实他和KMP的类似,借鉴了KMP构造next数组的思想,来构造fail指针。

看上图直接从左边的e跳转到右边的e,观察可以得出左边的he是一个单词的后缀,右边的he是一个单词的前缀,其实我们就是要在Trie树上找这种最长前后缀来构造fail指针。如果你懂了KMP的思想就知道为什么要这样构造fail指针,如果还是不懂,我也不准备展开,篇幅有限。
4 WM算法
多模式BM算法。嗯,姑且这样理解吧!
未完待续。。。