原理
原理最近暂时没有时间写。等我后面来补
引例1 给定一个长度为n序列a,有m次操作,操作分为两种,一是给出一个区间,求区间之和,二是给一个数加上一个值。
如果我们直接在数组a上做这个问题,区间和累加最多是O(n),而单点修改则是O(1);
如果我们考虑前缀和优化,那么区间和是O(1)的,而单点修改最坏则是O(n);
总的复杂度最坏都是O (mn),如果n和m都是10的5次方级别 显然会超时
是否存在更优秀的解法呢?
有!!!树状数组可以做到mlogn!!
假设 N = 2 ^ ik + 2 ^ ik - 1 + …… + 2 ^ i1;
其中 ik > ik - 1 > ik - 2 > ……> i1;
我们考虑把(0,N】这个区间拆分成以下的区间
- (x - 2 ^ i1,x];
- (x - 2 ^ i2 - 2 ^ i1, x - 2^i1]
- 一直到最后一个区间
- (0,x - 2 ^ i1 - 2 ^ i2 - 2 ^ i3 - …… - 2 ^ ik - 1]
注意以上区间均为左开右闭
以上区间的长度恰好为log(x),即x的二进制串长度
并且我们发现对于每个区间(l ,r】来说,区间的长度恰好为r的二进制数的最后一位1所对应的次幂
我们继续思考 如果我们要求一个区间【1,n】的总和,可不可以把这个大区间拆分成log(n)个小区间,先求出小区间之和,再累加到我们的大区间。
那么如何知道大区间所需要的小区间有哪些,又如何求小区间之和呢
首先我们已经知道了每个以r为右端点的区间长度,所以我们不需要知道左端点(因为我们可以自己求出来)
那么我不妨就以右端点为下标来表示区间
我们记 c[ r ] = [ r - lowbit(r)+ 1,r ];
lowbit是取一个二进制数的最小的一,也就是r所对应2进制数最后的一位1,不懂的可以蓝书从基础部分看起。可以O(1)求出
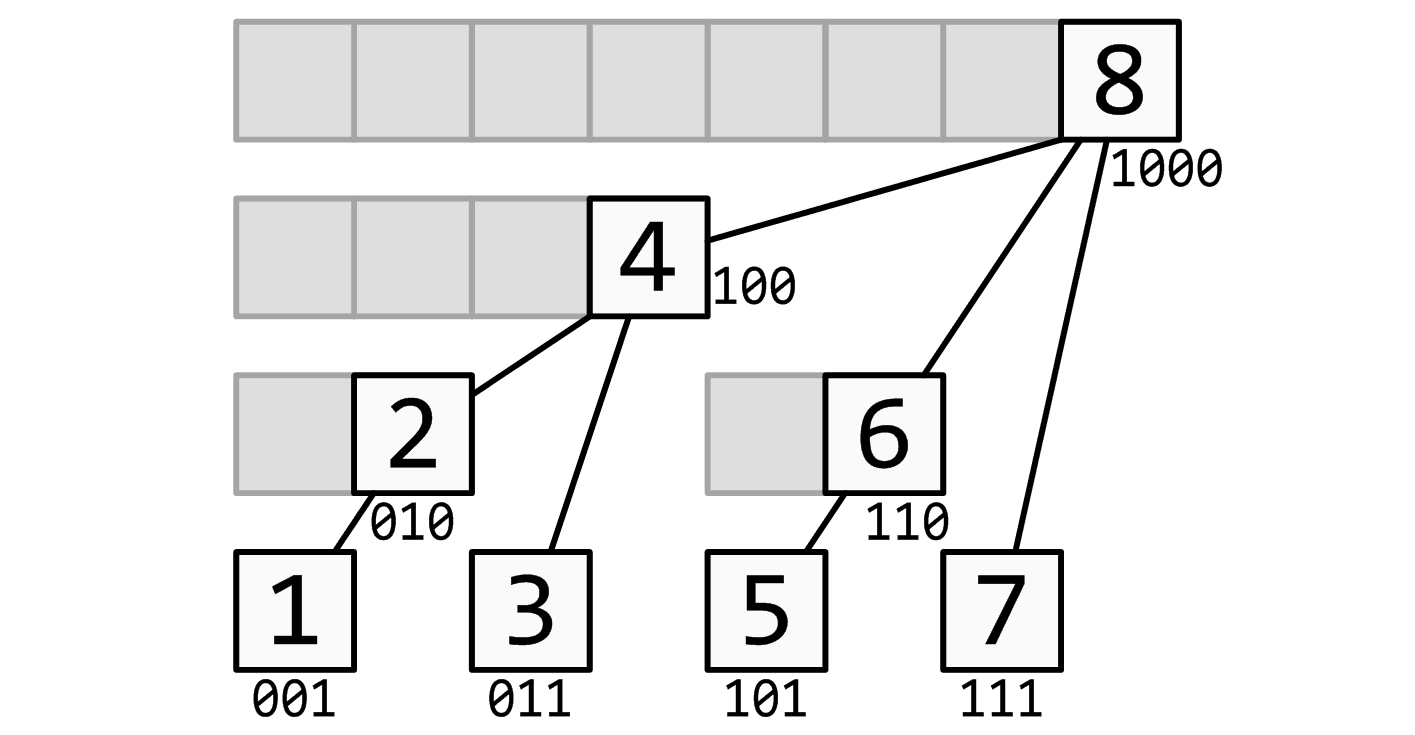
下面这张图以【1,8】这个区间为例;(摘自OI wiki)
我们发现c【1】 区间长度为1
c[ 2 ] 长度为2
c【3】长度为 1
c[4] 长度为4
不难发现所有奇数为右端点的区间长度均为1(原因是奇数的最后一位1恰好就是十进制下的1)
假设我们要求1 ~ 6的区间和
我们首先加上c【6】,然后我们发现还得加上c【4】
那c6和c4有什么关系呢? 注意 6 - lowbit(6)= 4,这真是太妙了!
所以我们只需要让一个区间右端点x 不断减去 自身的lowbit 直到它等于 0为止即可算出 1 ~x的区间和
既然1 ~ x的和算出来了,我们思考之前前缀和的思想
任意一个区间l ~ r也可以被算出来
而每次计算一个区间最多只要累加 log(n)次 太妙了!
我们再来看单点加,
显然只有包含当前节点的父节点的值会受到影响
而我们发现每个内部节点c【x】的父节点就是c【x + lowbit(x)】,不断做运算直到x > n即可。
单点修改(加)(log n)
void add(int x, int c) { for (int i = x; i <= n; i += lowbit(i)) tr[i] += c; }
区间求和(log n)
LL sum(int x) { LL res = 0; for (int i = x; i; i -= lowbit(i)) res += tr[i]; return res; }
引例2 把第一个问题的两种操作改成给一个区间加上一个给定的值,或是查询任意一个数的值
原先的问题是单点加和区间求和
而现在问题变成了区间加和单点查询
其实很容易想到差分,单点查询我们对差分数组求和一遍就可以了(logn),而区间加也只需要给两个点加上值即可(logn)
code:
#include<bits/stdc++.h> using namespace std; const int N = 100010; int tr[N]; int a[N]; int n,m; typedef long long LL; int lowbit(int x) { return x & -x; } void add(int x, int c) { for (int i = x; i <= n; i += lowbit(i)) tr[i] += c; } LL sum(int x) { LL res = 0; for (int i = x; i; i -= lowbit(i)) res += tr[i]; return res; } int main() { cin >> n >> m; for(int i = 1; i <= n; ++ i) scanf("%d",&a[i]); for(int i = 1; i <= n; ++ i) add(i,a[i] - a[i - 1]); while(m --) { string op; cin >> op; if(op == "C") { int l,r,d; scanf("%d%d%d",&l,&r,&d); add(l,d); add(r + 1,-d); } else { int x; scanf("%d",&x); printf("%lld ",sum(x)); } } }
引例3 在前面两个问题的数据范围内,能否同时做到区间求和和区间加呢
1.对于区间加来说,我们同样用到差分。
2.考虑区间和能否用到差分呢?我们会发现a1 + a2 + a3 + …… + ax
其实等于 b1 + b1 + b2 + b1 + b2 + b3 + ……+ bx;(可以在纸上画出来)
我们不妨把它补成一个长为x + 1,宽为x的矩阵,其中每行均代表 b1 + b2 + b3 + …… + bx
此时我们发现答案等于 (x + 1)Σ(i从 1 到 n)bi 减去 Σ(i从1到 n)(bi * i);
由此我们只需要开两个数组,分别维护前缀和即可。
代码:
#include <cstdio> #include <cstring> #include <algorithm> #include <iostream> using namespace std; const int N = 100010; typedef long long LL; LL tr1[N]; LL tr2[N]; int a[N]; int n,m; int lowbit(int x) { return x & -x; } void add(LL tr[],int x,LL c) { for(int i = x; i <= n; i += lowbit(i)) tr[i] += c; } LL sum(LL tr[],int x) { LL res = 0; for(int i = x;i; i -= lowbit(i)) res += tr[i]; return res; } LL prefix_sum(int x) { return (x + 1) * sum(tr1,x) - sum(tr2,x); } int main() { cin >> n >> m; for(int i = 1; i <= n; ++ i) scanf("%d",&a[i]); for(int i = 1; i <= n; ++ i) { int b = a[i] - a[i - 1]; add(tr1,i,b); add(tr2,i,1LL * b * i); } while(m --) { string op; int l,r,d; cin >> op; if(op == "C") { scanf("%d%d%d",&l,&r,&d); add(tr1,l,d); add(tr1,r + 1,-d); add(tr2,l,d * l); add(tr2,r + 1,-d * (r + 1)); } else { scanf("%d%d",&l,&r); printf("%lld ",prefix_sum(r) - prefix_sum(l - 1)); } } return 0; }