1.1 8
- 欧几里得算法还是会正常执行,也就是交换了两个数字。大的数字在前,小的数字在后。 该算法这种情况最多会发生1次。
1.1 12
- 因为每个门只会被它的约数开和关,所以只需要统计出每个门的约数的个数就可以了。然后判断约数的个数是奇数还是偶数
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int main()
{
int n; // n个带锁的门
cin >> n;
vector<int>v1,v2; // v1 代表这个门是开着的,v2代表这个门是关着的
for(int i = n;i >= 1;i --){
int cnt = 0;
for(int j = 1;j <= i;j ++){
if(i % j == 0){
cnt ++;
}
}
if(cnt & 1) // 该门被开了奇数次
{
v1.push_back(i);
}else{
v2.push_back(i);
}
}
reverse(v1.begin(),v1.end());
reverse(v2.begin(),v2.end());
cout << "门是开着的编号: " << endl;
for(int i = 0;i < v1.size();i ++){
cout << v1[i] << ' ';
}
cout << endl;
cout << "门是关着的编号: " << endl;
for(int i = 0;i < v2.size();i ++){
cout << v2[i] << ' ';
}
cout << endl;
return 0;
}
1.2 1
- 先把羊带过去,再把狼带过去,把羊在带回去,再把白菜带过去,最后把羊再一次带过去
1.2 2
- 甲乙,甲回,丙丁,乙回,甲乙。一共需要 2 + 1 + 10 + 2 + 2 = 17(分钟),符合题目要求
1.2 4
- 先判断判别式是否大于0,大于0有解否则无解

1.3 1
- a. 14 35 47 60 81 98
- b. 不稳定,这个会交换原来的顺序。
- c. 不在位,因为开了额为的数组,使用了额外的空间
1.3.4
- a. 这个问题简称为欧拉回路,就是从一个点出发,能否把每个点每条边补充不漏的走完,最终走回原点。
- b.
- 无向图存在欧拉回路的条件是所有的点的度数都是偶数,或者恰好有两个点的度数是奇数,则存在欧拉回路。若有奇数点度,则奇数点度点一定是欧拉路的起点和终点,否则可取任意一点作为起点。
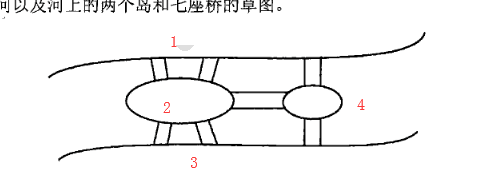
-
抽象为数学上的图

-
A号点的度数:3
-
B号点的度数:5
-
C号点的度数:3
-
D号点的度数:3
-
度数为奇数点的有4个,度数为偶数点的为0个,不符合条件。所以不能找到解决方案。
-
解决方案:已经知道有四个点的度数为奇数了,那么不能满足,1.只需让所有点的度数为偶数,加两条桥 2.让恰好两个点的度数为奇数。加一条桥。因为我们要加最少的所以我们只需要任意加一条桥就好了。