假目录
·网络流简介
·最大流
EK算法
·最小割
·Dinic
当前弧优化
最大流标程
·费用流
正确性证明
dijkstra费用流
标程
·上下界最大流
网络流简介:
有一个有向图,每条边为一条管道,有固定的容量,
从一个源点出发,它可以提供无限的水流,
流到一个汇点,它可以接受无限的水流,
每条边可以有一些水流通过,水流的大小不能超过容量,
我们把一个合法的解叫做一个流,一条边的水流大小叫做流量。
定义一条边的残量,是指它还能流多少流量(即容量减去当前流量)
性质:
1.容量限制:每条边的流量不超过其容量。
2.流量平衡:除源点和汇点外,对于每个点,流入它的流量和等于从它流出的流量和。
最大流:就是最大的流
最大化整个流的流量 ⇒ 最大化从源点流出的流量。
求解最大流:
一个贪心的思路:
每次从残量网络中任意找一条到达汇点路径,直到没有可以到达汇点的路径
然而它是错的
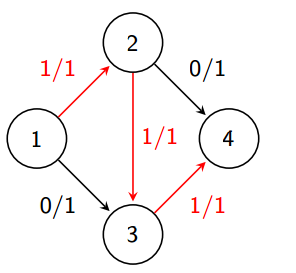
显然如果走了红色的路径,就不能再走其他的路径了
然而最优解是走上下两条路径。。
那么我们考虑“反悔操作”
我们想让水流“回去”,从而找到更优的解
一个可行的方法是建反向边
每次进行一次增流后,将正向边残联-流量,反向边容量+流量
显然,在反向边上增流,就相当于正向边上的流量减少,而且
总的残量是在不断减小的
上面的例子在找到1->2->3->4的路径后,图变为了这样:
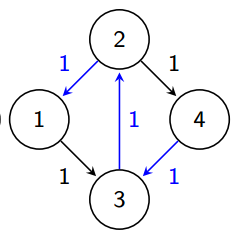
那么我们就又有了1->3->2->4一条路径,对它进行增广
于是就有了2的流量
这就是FF方法
1.在残量网络上找到一条从源点到汇点的道路(称为“增广路”)
2.取增广路上残量最小值v
3.将答案加上v
4.将增广路上所有边的残量减去v ,它们的反向边的残量加上 v。
由于残量网络不断在减小,它是一定会结束的
正确性之后会有证明
于是我们就可以为所欲为了
然而有时它会被卡

若走了1->2->3->4,

于是变成了这样

(明显抠图痕迹)
于是又有了一条1->3->2->4的路径
然后。。就被卡到了1100000000次
如何避免这种情况?
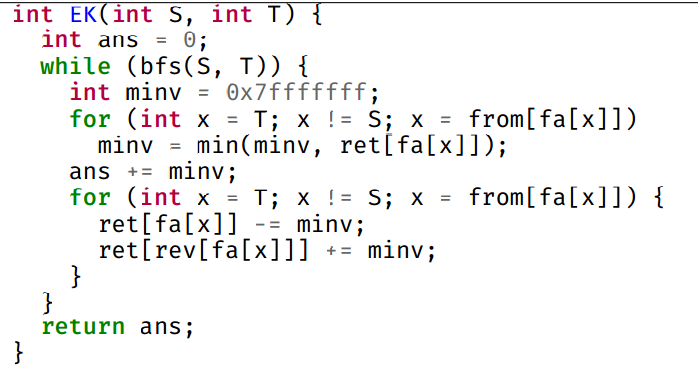
我们看一下EK算法:
——每次寻找最短增广路增广
每次增广的道路长度显然是不下降的,
所以不会被上面的极端情况卡掉
寻找最短路BFS即可
其复杂度是 O(m^2 * n)的
最小割
选出一些边的集合,
使得删除它们之后从源点无法到达汇点,
那么这个集合就叫做一个割。
这些边的容量之和称作这个割的容量。
最小割就是一个容量最小的割边集合
显然 ,任取一个割,其割的容量大于最大流的流量
最小割的容量等于最大流的流量,且FF方法能够正确的求出它
考虑 FF 算法结束时,残量网络上没有了增广路。
那么我们假设这时候,从源点经过残量网络能到达的点组成的集合为 X , 不能到达的点为 Y 。
显然汇点在 Y 里,并且残量网络上没有从 X 到 Y 的边。
可以发现以下事实成立:
1.Y 到 X 的边流量为 0 。如果流量不为 0 那么应该存在一条从 X 到 Y 的反向边,于是矛盾。
2.X 到 Y 的边流量等于其容量。只有这样它才不会在残量网络中出现。
根据第1个条件,我们可以得知:没有流量从 X 到 Y 之后又回到了 X 。
所以当前流量应该等于从 X 到 Y 的边的流量之和;
根据第2个条件,它又等于从 X 到 Y 的边容量之和。
所以FF方法也证明了是正确的。。
既然已经证明van了,我们进入下一环节
Dinic
EK算法每增广一条道路都要进行一次bfs,显然是比较慢的
考虑EK算法的优化:若增广后源点到汇点的最短路长度不变,不需要再bfs,直到最短路的长度变大再bfs
一次bfs找多个增广路径
增广时用dfs,记录下当前路径能允许的最大的流量,到达汇点时就统计

当前弧优化:
若在一次dfs中一些边已经访问过,在本次增广中就不会再产生新的贡献
于是我们直接跳过访问过的边
对于每个点维护一个“当前弧”cur[x],
表示从它开始的第一个可能可以增广的边是谁
for循环访问后将cur[x]置为最后的边i
每次for循环从cur[x]开始,而不是head[x]
bfs时将cur[x]置为head[x]

模板最大流Dinic+当前弧优化完整代码:

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 5 #define N 10010 6 #define M 200010 7 #define INF 0x3f3f3f3f 8 #define min(a,b) (a<b?a:b) 9 10 const int ch_top=4e7+3; 11 char ch[ch_top],*now_r=ch-1; 12 13 int n,m,s,t,ans; 14 15 int Head[N],to[M],w[M],next[M],num=1; 16 17 int deep[N],cur[N],que[N],head,tail; 18 19 inline void add(int x,int y,int v){ 20 to[++num]=y; 21 w[num]=v; 22 next[num]=Head[x]; 23 Head[x]=num; 24 to[++num]=x; 25 w[num]=0; 26 next[num]=Head[y]; 27 Head[y]=num; 28 } 29 30 inline int read(){ 31 while(*++now_r<'0'); 32 register int x=*now_r-'0'; 33 while(*++now_r>='0')x=x*10+*now_r-'0'; 34 return x; 35 } 36 37 bool bfs(){ 38 memset(deep,-1,sizeof(deep)); 39 head=tail=0; 40 deep[s]=0; 41 que[++tail]=s; 42 while(head<tail){ 43 int u=que[++head]; cur[u]=Head[u]; 44 for(int i=Head[u];i;i=next[i]){ 45 int v=to[i]; 46 if(deep[v]!=-1||!w[i]) continue; 47 deep[v]=deep[u]+1; 48 que[++tail]=v; 49 if(v==t) return 1; 50 } 51 } 52 return 0; 53 } 54 55 int dfs(int now,int cap){ 56 if(now==t||!cap) return cap; 57 int flow=0,f; 58 for(int i=cur[now];i;cur[now]=i=next[i]){ 59 int v=to[i]; 60 if(!w[i]||deep[v]!=deep[now]+1) continue; 61 if(!(f=dfs(v,min(cap,w[i])))) continue; 62 w[i]-=f; 63 cap-=f; 64 w[i^1]+=f; 65 flow+=f; 66 if(!cap) break; 67 } 68 return flow; 69 } 70 71 void Dinic(){ 72 while(bfs()) 73 ans+=dfs(s,INF); 74 } 75 76 int main() 77 { 78 fread(ch,1,ch_top,stdin); 79 n=read(); m=read(); s=read(); t=read(); 80 int x,y,v; 81 for(int i=1;i<=m;i++){ 82 x=read(); y=read(); v=read(); 83 add(x,y,v); 84 } 85 Dinic(); 86 printf("%d ",ans); 87 return 0; 88 }
费用流
现在每个管道使用要收费了,
收的费用=该管道收取的单位费用*该管道的流量
在保证最大流的情况下,求最小花费
解法:
建边时反向边的费用是正向边费用的相反数
每次按照费用求最短路增广
首先要保证一开始建的图没有负环
下证增广过程中没有负环:
如果增广过程中出现了负环

因为一开始没有负环,增广后负环一定是这样的:

图中b+(-a)<0,即出现了负环。
但是,b-a<0,b<a,那么上一次增广时的最短路应该是从u经过d的费用到v,产生矛盾
所以每次增广时选最短路是不会产生负环的。
正确性证明:
当前是最小费用流<=>当前残量网络无负环
因为残量有负环时,从负环上走一圈,可以得到更小的费用
这个东西反过来也是成立的。即如果有更小的解,一定存在一个负环来让我走一圈。
因为一般情况下费用相同的最短路不多,我们用EK算法进行增广
代码实现:将EK的bfs改成SPFA即可
最小费用最大流模板完整代码

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 #define N 5010 6 #define M 100010 7 #define INF 0x3f3f3f3f 8 #define reset(a,i) fill(a,a+1+n,i) 9 const int ch_top=4e7+3; 10 char ch[ch_top],*now_r=ch-1; 11 inline int read(){ 12 while(*++now_r<'0'); 13 register int x=*now_r-'0'; 14 while(*++now_r>='0')x=(x<<3)+(x<<1)+*now_r-'0'; 15 return x; 16 } 17 int n,m,s,t,Max_flow,Min_cost; 18 int Head[N],to[M],w[M],cost[M],next[M],num=1; 19 int pre[N],path[N],dis[N],que[N*100],head,tail; 20 bool inque[N]; 21 inline void add(int x,int y,int v,int c){ 22 to[++num]=y; 23 w[num]=v; 24 cost[num]=c; 25 next[num]=Head[x]; 26 Head[x]=num; 27 to[++num]=x; 28 cost[num]=-c; 29 next[num]=Head[y]; 30 Head[y]=num; 31 } 32 bool SPFA(){ 33 reset(path,0); reset(pre,0); 34 reset(dis,INF); reset(inque,0); 35 head=tail=0;dis[s]=0;que[++tail]=s; 36 while(head<tail){ 37 int u=que[++head]; inque[u]=0; 38 for(int i=Head[u];i;i=next[i]){ 39 int v=to[i]; 40 if(!w[i]||dis[v]<=dis[u]+cost[i]) continue; 41 dis[v]=dis[u]+cost[i]; 42 pre[v]=u;path[v]=i; 43 if(!inque[v]) inque[v]=1,que[++tail]=v; 44 } 45 } 46 if(pre[t]) return 1; 47 return 0; 48 } 49 void EK(){ 50 while(SPFA()){ 51 int f=INF; 52 for(int i=t;i!=s;i=pre[i]) 53 if(w[path[i]]<f) f=w[path[i]]; 54 Max_flow+=f; 55 Min_cost+=dis[t]*f; 56 for(int i=t;i!=s;i=pre[i]) 57 w[path[i]]-=f,w[path[i]^1]+=f; 58 } 59 } 60 int main() 61 { 62 fread(ch,1,ch_top,stdin); 63 n=read(); m=read(); 64 s=read(); t=read(); 65 int x,y,v,c; 66 for(int i=1;i<=m;i++){ 67 x=read(); y=read(); 68 v=read(); c=read(); 69 add(x,y,v,c); 70 } 71 EK(); 72 printf("%d %d ",Max_flow,Min_cost); 73 return 0; 74 }

然而SPFA被卡是标准操作
能不能用dijkstra求最短路呢?
dijkstra不能处理负权边,于是我们要想办法将负权边搞成非负的
考虑给每个点加一个“势”h[i],可以看做一个“高度”
在求最短路时将两点之间的费用看做cost[u][v]+h[u]-h[v]
我们可以发现,在一条从S到T的路径上,
除了S和T,其他点的“势”h[i]都在这个点的入边上减了一次,又在出边上加了一次
每个最短路都加上了h[S]-h[T],原来的最短路还是最短的
我们怎么求出这个h,是的所有的负边都成非负的呢?
设每条边的费用为ci,我们要让ci+h[u]-h[v]>=0
变形后:h[v]<=h[u]+ci
这。。貌似就是最短路。。
但是我们不能用最短路,因为我们正要求最短路。。
我们考虑用上一次的最短路作为h数组
这是可行的,下面给出证明:
若一条增广前残量不为0的边在增广后的残量仍不为零,
它仍然满足最短路的性质,dis[v]<=dis[u]+ci
若一条增广前残量为0的边在增广后残量不为零,
说明它的反向边被增广了,而且是最短路径
原先为一条u到v的边dis[v]=dis[u]+ci(因为是最短路上的边)
现在为一条v到u的边,边权为-ci
dis[u]=dis[v]-ci,dis[v]-dis[u]-ci=0,也是非负的
我们用前一次的dis作为当前的h数组时,因为dis[i]的值实际上是多了h[s]-h[i]的
所以h[i]=dis[i]-h[s]+h[i],而h[s]一直是0,所以可以写成h[i]+=dis[i]
dijkstra最小费用最大流模板完整代码

1 #include<algorithm> 2 #include<cstdio> 3 #include<queue> 4 #define N 5010 5 #define M 100010 6 #define INF 0x3f3f3f3f 7 #define reset(a,i) std::fill(a,a+1+n,i) 8 const int ch_top=4e7+3; 9 char ch[ch_top],*now_r=ch-1; 10 inline int read(){ 11 while(*++now_r<'0'); 12 register int x=*now_r-'0'; 13 while(*++now_r>='0')x=(x<<3)+(x<<1)+*now_r-'0'; 14 return x; 15 } 16 struct HA{ 17 int pos,cost; 18 }; 19 struct cmp{ 20 inline bool operator()(HA a,HA b){ 21 return a.cost>b.cost; 22 } 23 }; 24 std::priority_queue<HA,std::vector<HA>,cmp > q; 25 int n,m,s,t,Max_flow,Min_cost; 26 int Head[N],to[M],w[M],cost[M],next[M],num=1; 27 int pre[N],path[N],dis[N],h[N]; 28 bool vis[N]; 29 inline void add(int x,int y,int v,int c){ 30 to[++num]=y; 31 w[num]=v; 32 cost[num]=c; 33 next[num]=Head[x]; 34 Head[x]=num; 35 to[++num]=x; 36 cost[num]=-c; 37 next[num]=Head[y]; 38 Head[y]=num; 39 } 40 bool dijkstra(){ 41 for(int i=1;i<=n;i++)h[i]+=dis[i]; //将上一次的dis加到h中 42 reset(pre,0); reset(dis,INF); 43 reset(vis,0); dis[s]=0; 44 q.push((HA){s,0}); 45 while(!q.empty()){ 46 int u=q.top().pos; q.pop(); 47 if(vis[u]) continue; vis[u]=1; 48 for(int i=Head[u];i;i=next[i]){ 49 int v=to[i]; 50 if(!w[i]||vis[v]||dis[v] 51 <=dis[u]+h[u]-h[v]+cost[i]) //边权看做h[u]-h[v]+cost[i] 52 continue; 53 dis[v]=dis[u]+h[u]-h[v]+cost[i]; 54 pre[v]=u;path[v]=i; 55 q.push((HA){v,dis[v]}); 56 } 57 } 58 if(pre[t]) return 1; 59 return 0; 60 } 61 void EK(){ 62 while(dijkstra()){ 63 int f=INF; 64 for(int i=t;i!=s;i=pre[i]) 65 if(w[path[i]]<f) f=w[path[i]]; 66 Max_flow+=f; 67 Min_cost+=(dis[t]-h[s]+h[t])*f; //dis[t]多了h[u]-h[t] 68 for(int i=t;i!=s;i=pre[i]) 69 w[path[i]]-=f,w[path[i]^1]+=f; 70 } 71 } 72 int main() 73 { 74 fread(ch,1,ch_top,stdin); 75 n=read(); m=read(); 76 s=read(); t=read(); 77 int x,y,v,c; 78 for(int i=1;i<=m;i++){ 79 x=read(); y=read(); 80 v=read(); c=read(); 81 add(x,y,v,c); 82 } 83 EK(); 84 printf("%d %d ",Max_flow,Min_cost); 85 return 0; 86 }
上下界最大流问题
每条边除了容量,还限制了最小的流量
我们考虑把一条边拆开:
不妨设ei(u,v,l,h) 表示一条边ei起点为u,终点为v,最小流量限制为l,容量为h;

建一个超级源S和超级汇T,
将ei拆成三条边:
一条普通边从u到v,容量为h-l,即为最小限制之外的容量;
另一条边从S到u,容量为l;
另一条边从v到T,容量为l;

显然这三条边是和原来等价的,
S到T跑一遍最大流
在保证有解的情况下,S连出去的边和连入T的边一定都是满的,
否则无法满足最小流量的限制
再删去S和T
从原来的s和t跑一遍最大流,两次的值相加即可。
