manacher算法笔记

模板

【模板】manacher算法

不妨先只考虑如何求长度为奇数的回文串

记(P[i])表示以(i)为中心最多向两边扩展几个字符，满足回文

如串(ababa),

(P[1]=0,P[2]=1,P[3]=3,P[4]=1,P[5]=0)

如果暴力求解的话就是枚举每个中心位置，暴力判断能否扩展，在随机条件下跑不满，但是如(aaaaaaa)这样的串能卡到(O(n^2))

(manacher)算法

尝试利用以前求得的信息

还是一位一位的枚举，枚举到位置(i),记(maxr)为以(i)前面的字符为中心的回文串中最大的右端点位置，(k)为它的中心位置

如果(i<maxr)，(i)在这个回文串上 ，就可以知道i的字符与(k-(i-k))相同，P[k-(i-k)]至少为min(maxr-i,P[k-(i-k)]

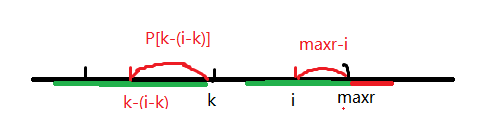
然后在暴力扩展就好了

复杂度：(maxr)最多移动(n)次，复杂度(O(n))

偶回文串：

把原字符串的每一位中间加一个特殊字符'#',以'#'为中心的奇回文串就对应原串中的偶回文串

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;

const int MAXN=22222222;

int n,p[MAXN];
char a[MAXN],s[MAXN];

int main()
{
	scanf("%s",a+1);
	n=strlen(a+1);
	s[0]='$';
	for(int i=1;i<=n;++i)
		s[i*2-1]='$',s[i*2]=a[i];
	s[n*2+1]='$';
	n=n*2+1;
	int mx=0,k=0,Ans=0;
	for(int i=1;i<=n;++i){
		if(i<=mx)
			p[i]=min(mx-i,p[k*2-i]);
		while(s[i+p[i]+1]==s[i-p[i]-1]) ++p[i];
		if(i+p[i]>mx) k=i,mx=i+p[i];
		Ans=max(Ans,p[i]);
	}
	printf("%d
",Ans);
	return 0;
}

【P1659】[国家集训队]拉拉队排练

先求(P)数组，每个(P[i])代表着长度为1~2*P[i]+1的回文串，区间加一可用差分维护，最后算一下前(k)大就行了

#include<iostream>
#include<cstring>
#include<cstdio>
#define int long long
using namespace std;

const int MAXN=1000010;
const int MOD=19930726;

inline int qpow(int x,int k){
	int s=1;
	while(k){
		if(k&1) s=s*x%MOD;
		k>>=1;
		x=x*x%MOD;
	}
	return s;
}

int n,k;
char s[MAXN];
int p[MAXN],diff[MAXN],a[MAXN];

signed main()
{
	scanf("%lld%lld%s",&n,&k,s+1);
	int mr=0,md=0;
	s[0]='$';
	for(int i=1;i<=n;++i){
		if(i<=mr) p[i]=min(mr-i,p[md*2-i]);
		while(s[i+p[i]+1]==s[i-p[i]-1]) ++p[i];
		if(i+p[i]>mr) mr=i+p[i],md=i;
	}
	for(int i=1;i<=n;++i)
		++diff[0],--diff[p[i]+1];
	a[0]=diff[0];
	for(int i=1;i<=n/2;++i)
		a[i]=a[i-1]+diff[i];
	int sum=0,Ans=1;
	for(int i=n/2;i>=0;--i){
		sum+=a[i];
		if(sum>=k){
			Ans=Ans*qpow(i*2+1,k-(sum-a[i]))%MOD;
			break;
		}
		Ans=Ans*qpow(i*2+1,a[i])%MOD;
	}
	if(sum<k)
		puts("-1");
	else printf("%lld
",Ans);
	return 0;
}