堆排序(Heap):
要讲堆排序之前先要来复习一下完全二叉树的知识。
定义:
对一棵具有n个结点的二叉树按层序编号,如果编号为i(0 <= i <= n)的结点与同样深度的满二叉树编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。

如上面就是一棵完全二叉树。
我们主要会使用的的性质是父结点与子结点的关系:
标号为n的结点的左孩子为2 * n + 1(如果有的话),右孩子为2 * n + 2(如果有的话)。
由于完全二叉树的结点的编号是连接的,所以我们可以用一个数组来保存这种数据结构。结点之间的关系可以通过上面的公式进行计算得到。
那什么是堆呢?
堆是具有下列性质的完全二叉树:
每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆(或大根堆);或者每个结点的值都小于或等于其左右孩子结点的值。称为小顶堆(小根堆)。

如图:就是一大根堆。将它转化为数组就是这样的:
{ 9,7,5,6,1,4,2,0,3 }
可以看到一个大概的情况是:第0个元素是最大的,前面的元素普遍比后面的大,但这不是绝对的比如例子中的1就跑到4前边去了。
建堆:
那接下来就是第一个问题了,怎么创建一个大根堆呢?也就是解决怎么将给定的一个数组调整成大根堆?
假如我们给定一个比较极端的例子{ 10,20,30,40,50,60,70,80 },加个0是为了方便不与结点的编号产生混淆。

对于这样的一个堆,我们应该怎么进行调整呢?
对于堆排序而言,一个比较直观的想法就是从下面开始,把值比较大的元素往上推。这样进行到根位置时,就可以得到一个一个最大的根了。
所以,我们应该从最后一个非叶子结点开始调整。
那么怎么确定哪一个是最后一个非叶子结点呢?
其实这完全是可以从完全二叉树的性质中得到的。还记得吗?
左孩子为2 * n + 1;
右孩子为2 * n + 2;
所以最后一个非叶子结点的编号为array.length / 2 – 1。array就是给定的数组。
所以我们第一个要调整的结点是编号为3的结点,拿它的值跟两个孩子的值做比较(它只有一个孩子)。显然,40和80这两个要交换位置了。

接下来就轮到编号为2的结点了,进行比较后显然是70比较大一点,也进行交换:

同样的道理,编号为1的结点也进行调节:
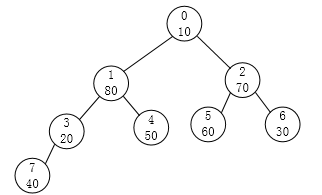
请注意,这个时候问题就来了。结点1是符合条件了,可以对于以结点3这根的这棵子树就不符合大根堆的要求了,所以我们要重新对编号为3的结点再做一次调整。得到:
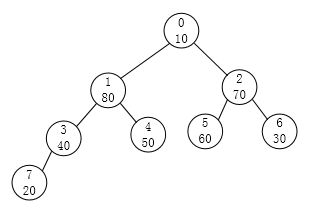
我们以同样的方法对编号为0的结点也进行同样的调整。最后就可以得到第一个大根堆了。

这一个过程我们可以称为建堆。我们将数据展开成数组:
{ 80,50,70,40,10,60,30,20 }
不难发现这一个过程中,我们已经把很多值比较大的数字也放到了比较靠前的位置。这一点相当重要,也可以说是堆排序的精华所在。
得到了大根堆之后,我们是可以得到一个最大值了,接下来要做的,就是不断的移除这个堆顶值,与堆尾的值进行交换,堆的长度减小1,然后进行重新的调整。

显然,每次都是在堆顶删除,在堆顶开始调整。

之后就是一直重复这个过程直到只剩下一个元素时,就可以完成排序工作了。
相信只要跟着这个思路和这几张图,自己模拟几次还是很好理解的。
接下来看看代码是怎么实现的:
public static void sort(int[] array) { init(array); // 这个过程就是不断的从堆顶移除,调整 for (int i = 1; i < array.length; i++) { int temp = array[0]; int end = array.length - i; array[0] = array[end]; array[end] = temp; adjust(array, 0, end); } } private static void init(int[] array) { for (int i = array.length / 2 - 1; i >= 0; i--) { adjust(array, i, array.length); } } private static void adjust(int[] array, int n, int size) { int temp = array[n]; // 先拿出数据 int child = n * 2 + 1; // 这个是左孩子 while (child < size) { // 这个保证还有左孩子 // 如果右孩子也存在的话,并且右孩子的值比左孩子的大 if (child + 1 < size && array[child + 1] > array[child]) { child++; } if (array[child] > temp) { array[n] = array[child]; n = child; // n需要重新计算 child = n * 2 + 1; // 重新计算左孩子 } else { // 这种情况说明左右孩子的值都比父结点的值小 break; } } array[n] = temp; }
堆排序的代码量比较多,主要的工作其实是在adjust上。
在adjust这个过程中有几个要注意的:
一个是要注意数组的边界,因为我们每次是把最大值放在最后,然后它就不能再参与调整了。
其次,是最后一个非叶子结点可能只有一个孩子,这也是需要注意的。
堆排序到底快在哪呢?
还是来看一个极端的例子:
{ 1,2,3,4,5,6,7 }
在建堆的时候第一次比较之后的结果应该是这样的:(7和3交换了位置)
{ 1,2,7,4,5,6,3 }
第二次调整之后是:
{ 1,5,7,4,2,6,3 }(5和2交换了位置)
然后是:
{ 7,5,1,4,2,6,3 }(7和1交换了位置,1的位置不对,需要再调整)
{ 7,5,6,4,2,1,3 }(6和1交换了位置)
可以看到,仅仅用了4次比较和4次交换就已经把数组给调整成“比较有序”了。
这个其实是由完全二叉树的性质决定的,因为子结点的编号和父结点的编号存在着两倍(粗略)的差距。
也就说父结点与子结点的数据进行一次交换移动的距离是比较大的(相对于步进)。这个与冒泡和直接插入的“步进”是有明显的区别的。可以说,堆排序的优势在于它具有高效的元素移动效率(这是个人总结,不严谨)。
其次,我们在调整堆的时候,可以发现有一半的数据是我们不用动到的。这就使比较次数大大地减少。这个就是很好地利用在建堆的时候保存下来的状态。还是那句话“让上一次的操作结果为下一次操作服务”。
最后回顾一下七个排序:
冒泡排序:好吧,它是中枪次数最多的,最大的优点应该是衬托其他算法的高效。
选择排序:我个人认为它是最符合人的思维习惯的,缺点在于比较次数太多了,但其实它在对少量数据,或者是对于只排序一部分(比如只选出前十名之类的),这种情况下,选择排序就很不错了,因为它可以“部分排序”。
直接插入排序:其实它还不算太差,在应对一些平时的使用时,性能还是可以的。直接插入排序是希尔排序的基础。
希尔排序:这个曾经把我纠结很久的算法,它的外表很难让人看出它的强大。它在几个比较高效的排序算法中代码是最少的,也很容易一次性写出。但理解有点困难。我觉得主要是那个步长序列太难让人一眼看出它到底做了些什么。个人觉得要理解希尔排序首先要弄清楚“基本有序”这个有什么用和希尔排序的前n-1个步长做的就是这些事。先让整个数组变得基本有序,基于一个事实,就是对于基本有序的数组而言,直接插入排序的效率是很高的。
归并排序:分治和递归的经典使用,胜就胜在元素的比较次数比较少(貌似说是最少的)。缺点是需要比较大的辅助空间,这个有时会成为限制条件(因为过大的空间消耗有时是不允许的)。
快速排序:如其名,虽存在一定的不稳定性,理论上在最差的情况下,快速排序会退化成选择排序,但可以通过一些手段来使这种情况发生的概率相当的小。
堆排序:个人觉得是最难一口气写出来的排序算法,特别是调整结点的算法每次都要写得小心翼翼(当然,可能是平时写得少)。但它确实是一个很优秀的排序算法,堆排序在元素的移动效率和比较次数上都是比较优秀的。操作系统中堆可是一个重要的数据结构。我记得当时第一次写出堆排序的感叹是“原来数组还可以这么用”。
最后让这几大高手进行一次PK吧,测试的数据是3000000个范围在0 ~ 30000000的随机数。
得到的结果大概是这样的:



差距并不算太大,可以看到,最快的还是Java类库提供的方法,它为什么能比快速排序还快呢?
因为它是综合了其他几个算法的特点,比如说在元素很少的时候,直接插入排序可能会快一点,数据量大一点的时候归并可能会快一点,当数据很大的时候,用快速排序可以把数组分成小部分。所以它不是一个人在战斗!
好了,至此,七个排序算法也算是复习了一次,还是那句话,本人菜鸟一个,对这几个算法理解有限,出错之处还请各位指出。
一点个人感受,算法这东西有时以为自己弄懂了,其实还差得远了,有时候看十次书不如自己写一次代码,写了十次代码不如跟别人讲一次。因为这个过程会遇到很多自己以前从没想过的事。这就是我写博客的初衷。