- 线性变化的几何表现
- 首先看下简单的矩阵,这是一个对角矩阵
M=(3001)
我们先用这个对角矩阵乘以一个点来看看它的几何变化。
(3001)∗(xy)=(3xy)
在几何上就相当于把原来的向量x轴方向拉伸成了原来的3倍
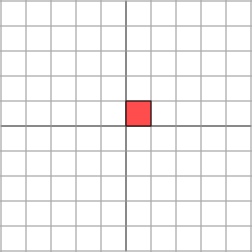 –》
–》
再来看下对称矩阵
M=(2112)
利用对称矩阵乘以一个点来看看它的几何变化 -》
-》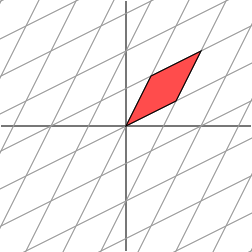
这并不能清晰的显示出发生了如何的几何变换。我们能够把整个坐标轴逆时针旋转45度来更好的发现规律。
 -》
-》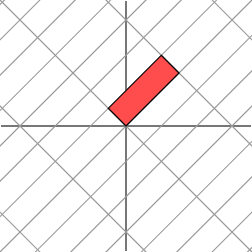
从上图能够看出原来的红色部分。沿着一个方向被拉伸了3倍。
- 神秘值分解
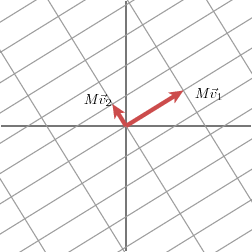
这是神秘值分解的几何实质:对于随意的二维方阵(M),我们都能够找到相互正交的向量 (v1,v2),使得经过M变换后得到的两个向量(Mv1,Mv2)还是正交的。
 -》
-》
对于随意的二维向量x
-那么我们怎么发现神秘值呢
我们能够对不论什么矩阵进行神秘值分解,首先我们先看下最先的样例,我们在原来的红色正方形上加上一个单位圆
 -》
-》
变化后的图形是个椭圆。我们我们能够在椭圆的最长和最短的方向上发现正交基
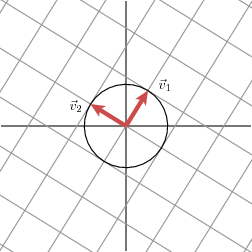 -》
-》
- 另外一个样例
利用M对v1 v2进行变换
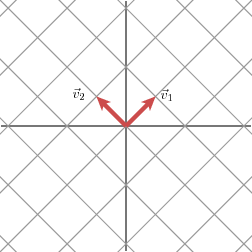 -》
-》
在这个样例中第二个神秘值为0,
M的秩是等于非0的神秘值的数目的。
- 数据压缩
神秘值分解能够有效地应用在数据表示中,如果我们来表示一个25*15的黑白像素

由于在整个图像中仅仅有3种列向量。所以我们能够来表示图像更加地高效



我们用一个25*15的矩阵来表示这个图像,1表示白色,0表示黑色

我们对M进行神秘值分解。仅仅发现了3个非0的神秘值
-噪音处理
如果我们利用了一个扫描器来扫描图像。可是在扫描的过程中引入了噪声

我们对这个25*15的矩阵进行神秘值分解

