算法导论10.顺序统计树与区间树习题

顺序统计树和区间树都是对红黑树的扩张：通过在节点添加字段完成其他的功能，如果该字段可以在 $O(1)$ 时间内维护，就能够不影响红黑树本身操作效率渐进量级。

顺序统计树

顺序统计树是红黑树的扩展：在红黑树的每个节点额外维护一个域size，记录以该节点为根的子树中的总结点个数。顺序统计数具有这样的功能：在 $O(\lg n)$ 时间内找到树中所有元素的第 $i$ 个顺序量。以下是一棵顺序统计树：

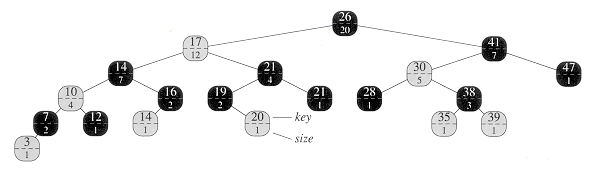
练习14.1-4 写出一个递归过程OS-KEY-RANK(T,k)使得顺序统计树T和某个关键字k为输入，输出k的秩（排序）。

思路：简单的递归：

• 如果关键字等于根节点，返回根节点左子树的size再加上1（这是根节点的秩）；
• 如果关键字小于根节点，返回该关键字在根节点左子树中的秩；
• 如果关键字大于根节点，返回该关键字在根节点右子树中的秩加上左子树的size加上1。

OS-KEY-RANK(r,k)if r = nil
        return 0
    if k < key[r]
        return OS-KEY-RANK(left[r],k)
    if k > key[r]
        return OS-KEY-RANK(right[r],k)+size[left[r]]+1
    if k = key[r]
        return size[left[r]]+1

练习14.1-5 给定含有 $n$ 个元素的顺序统计树中的一个元素 $x$ 和一个自然数 $i$，如何在 $O(\lg n)$ 的时间内找到元素 $x$ 的第 $i$ 个后继？

思路：就是中序遍历，但由于每个节点有size域，所以当子树里不可能符合条件时，可以直接跳过：

• 如果 $i=0$ 后继，直接返回 $x$ 本身；
• 如果 $x$ 右子树size大于等于 $i$ ，说明需要找的元素在右子树中，就采取OS-SELECT（题目中没有，正文中）方法找出右子树中第 $i$ 顺序量。
• 否则需要找的元素不在右子树中，就去找最近的祖先节点，且节点x必须在祖先节点的左子树中。对该祖先节点递归调用本方法，但是参数 $i$ 必须减去 $x$ 的右子树的size。这样理解：中序遍历中，会先遍历 $x$ 的右子树，再回到祖先节点上。
• 如果找不到左祖先节点，说明 $i$ 太大了，树中不存在这样的后继。

OS-SUCCESSOR(x,i)
    if i = 0
        return x
    if size[right[x]] < i
        t = size[right[x]]
        while s = father[x]
        if left[s] = x
            return OS-SUCCESSOR(s,i-t)
        if s = nil
            return nil
        x = s
    if size[right[x]] >= i
        return OS-SELECT(right[x],i)

练习14.1-7 说明如何在 $O(n\lg n)$ 时间代价内，利用顺序统计树对大小为 $n$ 的数组中的逆序对计数。 

思路：按照原数组的顺序，依次插入元素，构建顺序统计树。每次插入完成一个元素 $x$ 后，通过size域计算出该元素的顺序统计量 $i$（如练习14.1-4），进而得到在这棵顺序统计树中，比 $x$ 大的节点有多少个：这部分比 $x$ 大的节点实际上就与 $x$ 构成了逆序对，因为他们在 $x$ 之前插入了顺序统计树，说明在原数组中他们排在 $x$ 的前面。每插入一个元素之后就将该数目累加起来，最后求得逆序对的数目。

练习14.1-8 一个圆上有 $n$ 条弦，每条弦都是按照端点来定义的。给出一个能在 $O(n\lg n)$ 时间内确定圆内相交弦的对数。

思路：如果将圆从某个点剪断，并拉成直线，，圆上的所有县都变成了互相平行的线段，那么相交的弦的特点是：有重叠区域。每条弦有2个顶点，左端点和右端点，为每条弦创建一个代号，然后开始遍历2n个点：

• 如果是左端点，那么就将该端点对应的弦的代号，以左端点的位置为关键字，插入到顺序统计树中；
• 如果右端点，那么就将该端点对应的弦的代号从顺序统计树中删除。

在每条弦被删除之前，立刻统计一下树中现存的，关键字大于该弦的元素（如练习14.1-4）个数，这就是与待删除节点相交的弦的个数，因为这些弦：关键字值大于待删除的弦，说明其左端点在待删除弦的左端点右侧；在待删除弦马上就要被删除的时候，让然还没被删除，说明其右端点在待删除节点的右侧。所有而且仅有这样的弦与待删除的弦相交。

区间树

区间树是红黑树的另一种扩展，每个元素表示一个动态区间。红黑树用到的关键字值是区间树的区间左端点值。以下是一个区间树及其所表示的区间：

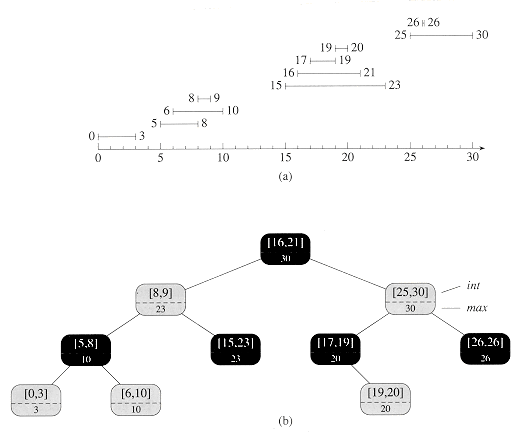
区间树的节点还扩展了一个域max，就是以该节点为根的子树的所有区间元素的右端点的最大值。该域很容易在 $O(1)$ 时间内维护：那就是左子结点的max、右子结点的max和自身区间的右端点三者的最大值。

区间树提供一些与区间有关的操作，比如判断一个区间有没有与区间树中的任何一个区间元素有交集，判断一个点是否落在区间树中的任意一个区间元素中。

练习14.3-6 说明如何维护一个支持操作MIN-GAP的动态数集Q，该操作能够给出Q中所有元素距离最近的两个。

思路：扩展红黑树，，将Q中的元素值作为关键字，在红黑树的每个节点上维护如下三个域：

• min-gap表示子树中所有元素，每两个元素中的最小距离；
• min表示树中所有元素最小值；
• max表示树中所有元素最大值。

问题的重点在min-gap域的维护上。min-gap应当这样维护：它应当是一下几个值得最小值：

• 左节点的min-gap域
• 右节点的min-gap域
• 左节点max域与本节点值的差
• 右节点min域与本节点值的差

练习14.3-7 VLSL数据库将一块集成电路表示为一个矩形，每个矩形的两边分别平行于x轴和y轴。给出一个算法，在 $O(n\lg n)$ 确定n个矩形中是否有两个有重叠区域。

思路：将n块矩形的左边界，右边界值排序为具有2n个元素的数组X，类似练习14.1-8，开始遍历X：

• 如果遍历到的元素x为某个矩形的左边界，那么将该矩形的上下边界作为一个区间插入到区间树中；
• 如果遍历到的元素x为某个矩形的右边界，那么将该矩形的上下边界区间从区间树中删除。

在删除区间之前，判断一下在区间树中是否有其他元素和待删除的区间有重叠区域。如果有，则找出了重叠区域。数组X已排序，并且插入和删除顺序保证了两个矩形在x轴上有重叠，而区间树保证了两个矩形在y轴上有重叠，因此两个矩阵有重叠区域。

思考题14-1 有一组区间，如何尽可能快地找到最大重叠点：即与该点有重叠区域的区间的数目最多。

思路：直观上，最大重叠点一定可以是端点，因为最大重叠点和非最大重叠点的分界，一定是某个区间具有端点造成的。这样考虑：

1. 将所有端点组织成红黑树，增加一个域p，左节点为1，右节点为-1。
2. 然后在节点中再维护一个域s，表示以该节点为根的子树中所有元素的p的和。某个节点的重叠数就是该节点左节点的s域：因为s表示，在这个节点上，已经开始（+1）但没有结束的（-1）的区间的个数。s域的维护也很简单，就是左子树的s加上右子树的s再加上自身的p。
3. 最大重叠数也维护在节点中，为域m，表示以该节点为根的子树中所有元素的最大重叠数。m的维护是：m为左节点的最大重叠数、右节点的最大重叠数和自己的最大重叠数三者的最大值。

思考题14-2 Josephus环。假设n个人排成一圈，给定一个正整数m<n，从某人开始报数，遇到第m个人就让其出圈，并进行下去直到所有人出圈，给出一个算法来获得这n个人出圈的顺序。

1. 如果m是个常数，那么在$O(n)$内。
   用环形链表也好，因为$m=O(1)$，所以直接遍历每个元素，每m次删除一个元素，获得出圈序列的一个值。
2. 如果m不是常数，那么在$O(n\lg n)$内。
   顺序统计树最重要的意义是，可以在$O(\lg n)$时间内访问第$i$顺序量（注意$i$不是常数）。第1问中，实际上遍历了mn次，但m是常数，所以效率还是$O(n)$。而在这里，m不是常数，因此可以将所有元素组织成顺序统计树，每次访问并删除一个节点的耗费是$O(\lg n)$，总耗费就是$O(n\lg n)$。