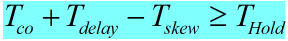1 模型分析
理解建立时间保持时间需要一个模型,如下图所示。

图:触发器时钟和数据模型
时钟沿到来时采样数据D,将采到的数据寄存下来,并输出到Q端,所以如果没有新的时钟沿到来,则Q端输出的一直是上次采样的数据,每来一个时钟沿,采样一次数据D。那么分析这个建立时间和保持时间,我们分两种情况,一种是clka没有传输延时(clock skew),一种是由传输延时,前者相对容易一些。

图:建立时间和保持时间
建立时间太短或者保持时间不够,均不能在clk的上升沿采集到正确的数据。
后面分析需要用到的参数:
Tco: 数据正确采样后从D端到达Q端的延时,触发器固有属性,不可改变
TDelay: D1输出端到D2输入端的组合逻辑延时和布线延时
Tsu: 触发器的建立时间,触发器固有属性,不可改变
Th: 触发器的保持时间,触发器固有属性,不可改变
Tclk: 时钟周期
t1: 假设源时钟为clka,clka到达D1的延时
t2: 同t1,是clka到达D2的延时
2 无传输延迟下的建立时间和保持时间
2.1 时钟和数据模型
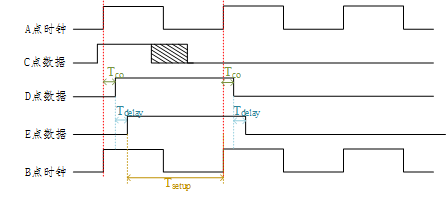
2.2 建立时间

2.3 保持时间
我们假设组合逻辑的Delay延迟非常大,如下图所示。
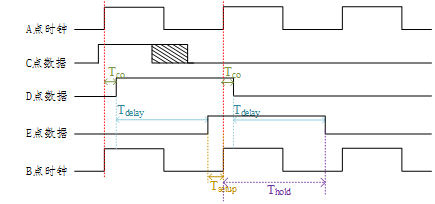

3 有传输延迟下的建立时间和保持时间
事实上Clock的传输也是有延时的,如图所示,两个触发器的源时钟为clka,到达D1需要t1的时间,到达D2需要t2的时间,t2−t1t2−t1其实就是我们常说的clock skew(时钟偏斜),就是同一个时钟沿达到D1和D2的时延差别,如果D1和D2离的很远,那么相应的clock skew就会更大。
3.1 时钟和数据模型
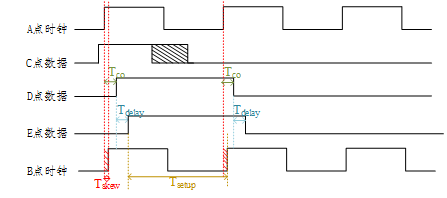 3.2 建立时间
3.2 建立时间
红色部分是时钟偏移t2-t1,建立时间的关系式:
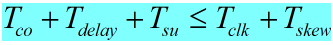
3.3 保持时间
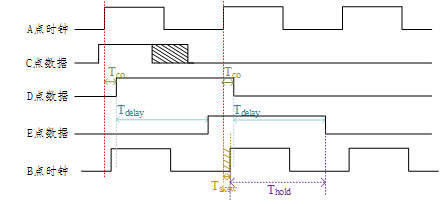
图中假设组合逻辑延迟很长,棕色部分是时钟的延迟,就是t2-t1的时间差,保持时间如下式: