branch指令只有进入decode阶段,CPU才能知道是否跳转。Branch进入到ALU阶段,CPU才知道是否taken。

有什么方式可以降低这种flush掉没用的指令。CPU不知道会不会跳转,以及不知道会跳转到哪里去。如果在TETCH有可以预测branch是否taken,或者知道taken之后的下一条指令,效率提高。怎么去做到branch。
如何预测?
1.该指令是否是branch指令?
2.判断是否taken。
3.如果taken,目标地址在哪里?
对CPI的影响?
CPI = 1+(mis-predicted/instructions)*penalty
其中penalty就是要Flush掉的指令数量。
下面一个例子:

1+0.1×0.2×2=1.04是什么意思?
90%的指令预测准确率,那么有0.1的概率错误预测,0.2表示有20%的指令是Branch,2代表有2条指令被Flush掉。
可见在流水线级数很长的情况下,branch的精确度对性能影响非常大。
预测branch的思路?

一条指令执行的模式是由规律的,这里用到branch的历史执行方式。
Branch Target Buffer BTB概念,用来存放Branch目标的,当然,已经知道branch是被taken的。Branch目标地址就存放在BTB中,如果该次没预测对,那么就会更新BTB中的PCnext。如何设计BTB,就是越快越好,那么这个buffer尽可能小。使用PC的低10bit作为BTB的entry。因为正常程序在执行的时候,地址每次加4,也就是只有低bit在改变。
简单的预测banch的方法。1bit 预测。解决branch是否taken。

也就是,现在有条branch指令,走到ALU阶段,这条branch被执行了,然而上次branch没被执行,BHT中存放的是0:Branch is not taken,这是就修改BHT中的值为1:Branch is taken。那么下次在执行Branch的时候,我们预测他会被执行。
1bit预测的优劣。当一条branch总是taken或者taken远大于不taken,或者正好相反,那么1 bit预测就可以工作很好。但是如果taken 和not kaken次数差不多时候,这个1 bit预测就不管用了。
2bit 预测,和1bit预测原理差不多,只是多了2种情况。
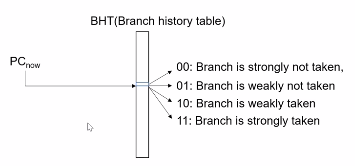

一条强烈不执行的branch被taken了,那么就会进入weakly not taken状态,下次就是直接进入可能不执行的状态,但是下次真的没执行,那么就回到强烈不执行状态;如果被taken了,那么进入到可能执行的状态。相比于1 bit预测,从not kaken到taken,需要两次branch taken。
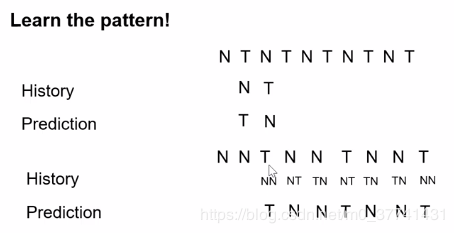
从图中可以看出,当前两条为NN的时候,那么下一条CPU就预测为Taken;当前两条为Not Taken和Taken的时候,那么下一条预测为Not Taken。基于历史来做预测,准确度会更高。
CPU一般是基于2-bits history predict来做的。
对于函数的返回值指令,如何预测呢?
0x1230: Call FUN
.
.
.
0x1250: Call FUN
FUN:
RET
PC到0x1230,调用FUN ,FUN执行完后执行RET,回到1230地址,在BTB中更新为1230地址;当程序执行到1250后,有调用FUN,再执行RET,之前BTB已经更新RET为1230,而不是1250,这样子会导致mis-predict(本应该回到1250),这时BTB会更新到1250;如果程序LOOP到1230,那么每一次branch按照BTB的预测都会失败。解决这个问题,引入RAS(Return address stack),采用栈的方式解决。执行0x1230的时候,把0x1230push到栈中,RET的时候从栈中取0x1230,当从0x1250调用FUN的时候,把0x1250push到栈中,RET的时候,从栈中调取0x1250。