今晚分享平衡二叉树 所以下午预习了一下
还有红黑树 不过目前脑袋有点炸,晚上或者明天再看吧
好 下面开始
首先说明自己的参考来源:点击这里
学习平衡二叉树之前,先学习二叉排序树。
BST
二叉排序树(Binary Sort Tree)又称二叉查找树。
它或者是一棵空树;或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3)左、右子树也分别为二叉排序树;
举一个例子理解一下
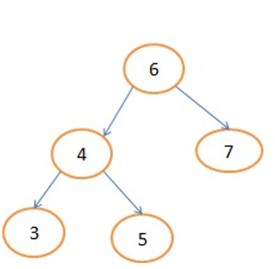
创建的结构体如下:
typedef struct _BitNode { int data; struct _BitNode *lchild,*rchild; }BitNode,*BiTree;
左右子树的指针和节点的值。
查找的时候从根节点开始,根据大小查询左右子树。
直到查询为空或查询到目标节点
具体增删改查等操作移步上面参考的文档进行查看
AVL
下来说明平衡二叉树
平衡二叉树定义(AVL):
它或者是一颗空树,或者具有以下性质的二叉树:
它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1,
且它的左子树和右子树都是一颗平衡二叉树。
定义:平衡因子(bf):结点的左子树的深度减去右子树的深度,那么显然-1<=bf<=1
定义结构体
typedef struct _BitNode { int data; int bf;//平衡因子 struct _BitNode *lchild,*rchild; }BitNode,*BiTree;
平衡二叉树的目的是为了减低操作时间复杂度
下面用两张图比较就可以很好理解了
同样查询10这个节点 图一(AVL)一定是比图二(BST)要快的
平衡二叉树的主要操作分为左旋和右旋
根本目的是在不改变二叉排序树的前提下,把其改成AVL 同时也在插入和删除操作后进行格式的恢复

这个图节点4的深度为2需要进行右旋操作:
让4节点的左孩子指向3的右子树(此时为NULL),让3的右孩子指向4,让树根指向3
代码
void R_Rotate(BiTree&T) { BiTree p; // p=T->lchild; //假如此时T指向4,则p指向3; T->lchild=p->rchild; //把3的右子树挂接到4的左子树上(此例子3右子树为空) p->rchild=T; //让3的右孩子指向4. T=p; //根指向节点3 }
最终结果:
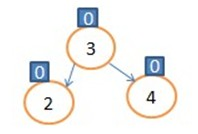
下一个例子:
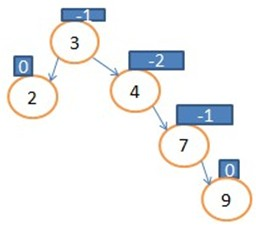
图中标识有点错误,3节点的平衡因子是-3
这里我们修改平衡因子为-2的节点 进行左旋操作
那我们就把4的右孩子7的左子树(此时为NULL),让7的左孩子指向4,让3的右孩子指向7
最终结果:
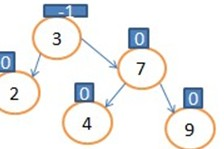
接下来说明一种特殊情况
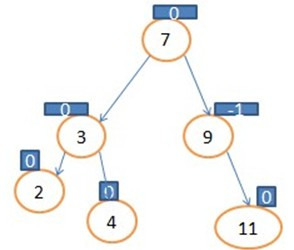
在这个树的基础上增加10这个节点

这样显然是不对的
进行左旋操作
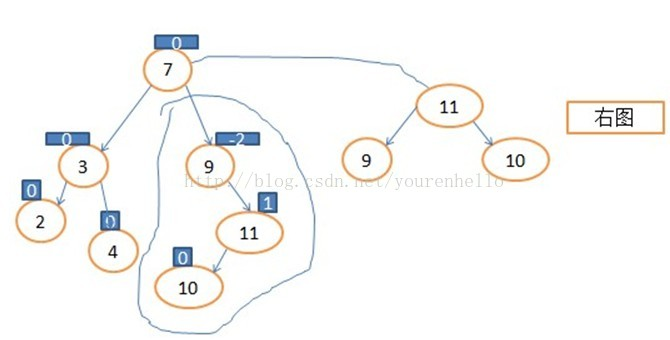
咦 更不对了! 10怎么跑到11的右边了
BUG!
其实不是的,大家注意到9的平衡因子-2 、10的平衡因子1
符号不同的情况下就会出现错误
我们应先修改11的符号
首先对11进行右旋,再对9进行左旋

Over
剩下的代码找之前那个参考的吧
以上是我个人理解,有问题请留言,看到后会尽快回复
一同交流进步。
