数据结构 树(上)
一、概述
主要内容包含树的基本概念、二叉树(平衡二叉树、完全二叉树、满二叉树)、搜索树(二叉搜索树、平衡搜索树、AVL树、伸展树、(2,4)树、红黑树)、(a,b)树、B树等实际运用的树数据结构
二、基本知识(树的定义和属性)
1、树(非线性数据结构)运用于一些算法实现的效率会比线性数据结构(基于数组的列表和链表)快,广泛运用于文件系统目录结构、图形用户界面、MySQL数据库索引、网站、路由协议和其他计算机系统中
2、树T定义为存储一系列元素的有限节点集合,这些节点具有 parent-children 关系且满足属性:一、如果树T不为空,则它一定具有一个称为根节点 r 的特殊节点,并且该节点没有父节点;二、每个非根节点 v 都具有唯一的父节点 w ,每个具有父节点 w 的节点都是节点 w 的一个孩子
3、一个没有孩子的节点 v 称为外部节点或者叶子节点,一个有一个或多个孩子的节点 v 称为内部节点
4、树的边:一对具有父子关系的节点(u,v);树的路径:一系列节点,这些节点中任意两个连续的节点都具有父子关系
5、节点P的祖先:从根节点到该节点P所经路径上的所有节点;节点P的子孙:以该节点P为根节的子树中任意一个节点都是节点P的子孙
6、有序树:如果树中的每个节点的孩子节点都有特定的顺序,称为有序树。有序树:二叉树、霍夫曼树(信息编码)、B树(一种对读写操作进行优化的自平衡的二叉查找树)
7、树的底层存储的方式有链表和数组两种。数组存储方式存访问速度快,但是插入和删除节点操作时间复杂比链表高。实际中更多的是用链来存储树
8、树T中节点P的深度:节点P的祖先的个数(不包括P本身)递归定义:如果P是根节点,P的深度是0;否则,P的深度是其父节点深度加1
9、树T中节点P的高度:如果P是叶子节点,P的高度是0;否则,P的深度是其孩子节点中最大高度加1。树T的高度是根节点的高度!高度=路径上的“边数”=路径上的节点数-1
10、节点的度:节点含有子树的个数称为这个节点的度;树的度:最大的节点的度称为树的度
def _height1(self): # works but O(N^2)worst-case time
"""return the height of the tree"""
return max(self.depth(p) for p in self.positions() if self.is_leaf(P))
def _height2(self,p): # time is linear in size of subtree
"""return the height of the subtree rooted at Position p"""
if self.is_leaf(P):
return 0
else:
return 1+ max(self.height2(c) for c in self.children(p))
三、树的抽象数据类型
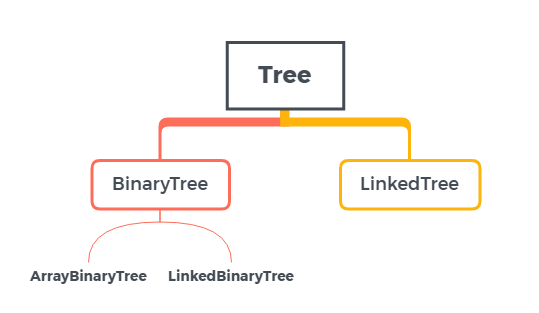
Tree抽象基类(没有完整的内部细节描述,也没有实现一些必要的行为)
一、Tree抽象基类,BinaryTree类继承Tree抽象基类,保持抽象性
1、p.element( ):返回存储在位置p中的元素
2、T.root( ):返回树T的根节点位置,如果根节点为空,返回None
3、T.is_root( P):判断位置P是否为树T的根节点,如果是,返回True
4、T.parent( P):返回位置为P的父节点的位置,如果位置P为根节点,返回None
5、T.num_children( P):返回位置为P的孩子节点的编号
6、T.children( P):产生位置为P的孩子节点的一个迭代
7、T.is_leaf( P):如果位置P没有任何孩子,返回True
8、len(T):返回树T包含的元素的数量
9、T.is_empty( ):如果树T不包含任何节点,返回True
10、T.positions( ):生成树T的所有位置的迭代
11、iter(T):生成树T中存储的所有元素的迭代
12、T.left(p ):返回p左孩子的位置,若p没有左孩子,返回None
13、T.right(p ):返回p右孩子的位置,若p没有右孩子,返回None
14、T.sibling(p ):返回p兄弟节点的位置,若p没有兄弟节点,返回None
15、T.add_root(e):创建新的根节点,存储元素e,并返回根节点位置。若树非空,抛出错误
16、T.add_left(p,e):创建新的节点,存储元素e,并将该节点链接为位置P的左孩子。若位置P的左孩子非空,抛出错误
17、T.add_right(p,e):创建新的节点,存储元素e,并将该节点链接为位置P的右孩子。若位置P的右孩子非空,抛出错误
18、T.replace(p,e):用元素e替换在位置p的元素,返回之前存储的元素
19、T.delete(p):移除位置p的节点,用他的孩子替代自己,若有,返回存储在位置p的元素;若p有两个孩子,抛出错误
20、T.attach(p,T1,T2):将树T1,T2分别链接到T的叶子节点P的左右子树,并将树T1,T2重置为空树;若p不是叶子节点,抛出错误
四、二叉树(Binary Tree)
一、基本知识
1、二叉树是具有要求属性的有序树:一、每个节点最多有两个孩子节点;二、每个孩子节点被命名为左孩子或右孩子;三、每个节点的孩子,在顺序上,左孩子先与右孩子
2、满二叉树:所有叶结点同处于最底层(非底层结点均是内部结点),一个深度为k(>=-1)且有2^(k+1) - 1个结点(k=-1表示空树)
3、完全二叉树:叶子节点只能出现在最底层的两层,而且最底层的叶子节点均处于次底层叶子节点的左侧。除了最后一个叶子节点的父节点外,若每个节点都有零个或两个子节点。
4、平衡二叉树:是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树
5、二叉搜索树(排序二叉树)
6、平衡二叉树的常用实现方法有 AVL、伸展树、红黑树、替罪羊树、Treap等
7、二叉树的属性:非空二叉树T的节点数n、外部节点数nE、内部节点数nI、高度h(h+1≤n≤2h+1-1)、log(n+1)-1≤h≤ n-1;完全二叉树:log(n+1)-1≤h≤(n-1)/2
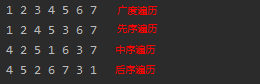
8、二叉树遍历:层次遍历(广度遍历);深度遍历:中序遍历(左子树>>根节点>>右子树)、先序遍历(根节点>>左子树>>右子树)、后序遍历(左子树>>右子树>>根节点)
二、基于链式存储结构的二叉树的实现和二叉树抽象基类支持的增加元素方法和遍历方法:add( )、breadth_travel( )、preOrder( )、inOrder( )、postOrder( )
1、定义二叉树的节点类:class Node。以下为单向链表,双向链表增加 self.parent=None,指向父节点的引用,如果节点是根节点,该引用指向None
class Node(object):
def __init__(self, item):
self.elem = item
self.lchild = None
self.rchild = None
2、定义二叉树按照完全二叉树添加元素方法:Tree.add( )
class LinkedBinaryTree(object):
def __init__(self):
self.root = None
def add(self, item):
node = Node(item)
if self.root is None:
self.root = node
return
# 使用队列FIFO,迭代查询
queue = [self.root]
while queue:
cur_node = queue.pop(0)
if cur_node.lchild is None:
cur_node.lchild = node
return
else:
queue.append(cur_node.lchild)
if cur_node.rchild is None:
cur_node.rchild = node
return
else:
queue.append(cur_node.rchild)
3、定义二叉树层次遍历(广度优先遍历)方法:Tree.breadth_travel( )
3.1、广度优先遍历的运行时间为O(n)
def breadth_travel(self):
if self.root is None:
return
queue=[self.root]
while queue:
cur_node=queue.pop(0)
print(cur_node.elem, end=' ')
if cur_node.lchild is not None:
queue.append(cur_node.lchild)
if cur_node.rchild is not None:
queue.append(cur_node.rchild)
4、深度遍历:先序遍历preOrder( )、后序遍历postOrder( )、中序遍历inOrder( )
4.1、先序遍历和后序遍历的整体运行时间为O(n),n是树中位置的数量
4.2、中序遍历是针对于二叉树的遍历算法,有几个重要的应用如:表示算术表达式(叶子节点表示参数,内部节点表示运算符)、中序遍历算法将有序的序列的元素存储在二叉树
def preOrder(self, node):
"""先序遍历"""
if node is None:
return
print(node.elem, end=' ')
self.preOrder(node.lchild)
self.preOrder(node.rchild)
def inOrder(self, node):
"""中序遍历"""
if node is None:
return
self.inOrder(node.lchild)
print(node.elem, end=' ')
self.inOrder(node.rchild)
def postOrder(self, node):
"""后序遍历"""
if node is None:
return
self.postOrder(node.lchild)
self.postOrder(node.rchild)
print(node.elem, end=' ')
5、测试代码
if __name__ == '__main__':
node = Tree()
node.add(1)
node.add(2)
node.add(3)
node.add(4)
node.add(5)
node.add(6)
node.add(7)
node.breadth_travel()
print('')
node.preOrder(node.root)
print(' ')
node.inOrder(node.root)
print('')
node.postOrder(node.root)
print('')
6、输出结果
三、基于数组表示的二叉树
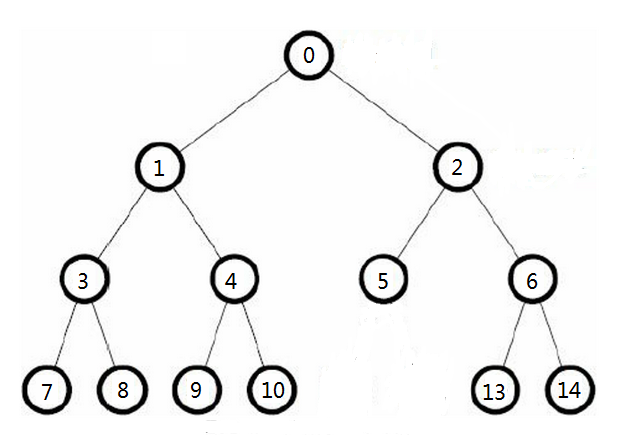
1、基于数组表示的二叉树的表示方法是对T的位置进行编号。
2、T中每个位置p的编号 f(p):若p是根节点,则 f(p)=0;若p是位置q左孩子,则 f(p)=2f(q)+1;若p是位置q右孩子,则 f(p)=2f(q)+2
3、基于数组表示的空间的使用情况极大地依赖于树的形状,数组A所需要的长度N=1+fM。fM为f(p)中的最大值。数组A可以有多个空单元,未指向T的已有节点
4、最坏的空间需求N=2n-1,而且树的更新操作(删除、增加等)的时间复杂度是O(n)
5、基于数组表示的二叉树

五、二叉搜索树
一、基本知识
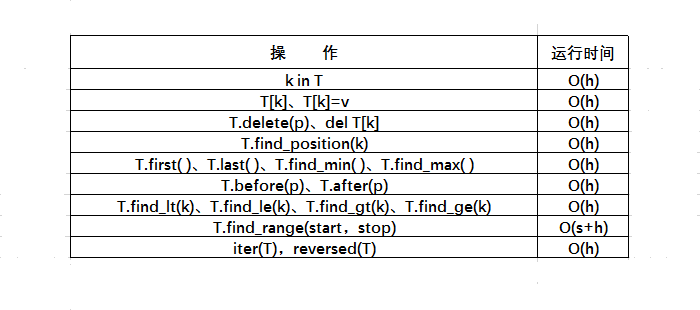
1、树形数据结构的一个重要的用途是用作搜索树。搜素树结构有效地实现有序映射!(M[k]、M[k]=v、del M[k])
2、二叉搜索树:每个节点p存储的是一个键值对(k,v)的二叉树T,且满足键的位置结构特性:一、存储在p的左子树的键都小于k;二、存储在p的右子树的键都大于k
二、二叉搜索树的遍历M[k]
1、存储有序的序列的二叉搜索树中进行中序遍历算法:先左子树的递归地进行中序遍历会在孩子树上以递增的顺序产生键的迭代,然后根节点的访问,最后是右子树的递归进行中序遍历会在孩子树上以递增的顺序产生键的迭代。中序遍历可以在线性时间内被执行,对二叉搜索树进行中序遍历时,可以在线性时间内产生一个映射中所有键的有序迭代!
2、二叉搜索树实现更细粒度的遍历,直接定位到指定元素节点:frist():返回包含最小键的节点,如果树为空,则返回None;last():返回包含最大键的节点,如果树为空,返回None;before(p)p的前驱节点:返回比节点p的键小的所有节点中键最大的节点,如果p是第一个节点,返回None(中序遍历在p之前最后一个被访问的节点--p的左子树中最右节点,如果没有左子树,p在父节点的右子树,则是p的父节点);after(p)p的后继节点:返回比节点p的键大的所有节点中键最小的节点,,如果p是最后一个节点,返回None(中序遍历在p之后第一个被访问的节点--p的右子树中最左节点,如果没有右子树,p在父节点的左子树,则是p的父节点)
3、二叉搜索算法:TreeSearch在路径上各个节点被调用,每个调用执行恒定数量的基本操作O(1)。节点的数目被设定为h+1(h+1次调用),h为T的高度,所以总的搜索时间是O(h)
6、非空二叉树T:log(n+1)-1≤h≤ n-1;完全二叉树:log(n+1)-1≤h≤(n-1)/2,n为T的节点总数、h为高度,各种策略,是得搜索树T的高度上限是logn!
def TreeSearch(self, T, p, k):
if k == p.key():
return p
elif k < p.key() and T.left(p) is not None:
return self.TreeSearch(T, T.left(p), k)
elif k > p.key() and T.right(p) is not None:
return self.TreeSearch(T, T.right(p), k)
# unsuccessful search
return p
三、二叉搜索树的插入和删除M[k]=v、del M[k]
1、M[k]=v:TreeSearch()遍历树T。如果存在k,则重新给节点赋值为v;如果不存在,即遍历最后子树为None,则在该位置插入新的节点(k,v)
def TreeInsert(T, k, v):
p=TreeSearch(T, T.root(), k)
if k == p.key() then
Set p's value to v
elif k < p.key() then
add node with item(k,v) as left child of p
else:
add node with item(k,v) as right child of p
2、del M[k]:情况一、存储k的节点p只有一个孩子:删除节点p,并用孩子节点代替p;
-----------------情况二、存储k的节点p有两个孩子:一、r=befor(p),二、r替代p,三、由于r=befor(p)而且p有两个孩子,所以r是p左子树中最右节点,即没有右子树,按照情况一删除-----------------树中原来r位置的节点
四、二叉搜索树性能
五、python代码
# node in-order traversal(LDR)
def traversal(node):
if not node:
return
traversal(node.lchild)
print(node.value,end=' ')
traversal(node.rchild)
# insert node
def insert(root, value):
if not root:
return Node(value)
if value < root.value:
root.lchild = insert(root.lchild, value)
elif value > root.value:
root.rchild = insert(root.rchild, value)
return root
# delete node
def delete(root, value):
if not root:
return None
if value < root.value:
root.lchild = delete(root.lchild, value)
elif value > root.value:
root.rchild = delete(root.rchild, value)
else:
if root.lchild and root.rchild: # degree of the node is 2
target = root.lchild # find the maximum node of the left subtree
while target.rchild:
target = target.rchild
root = delete(root, target.value)
root.value = target.value
else: # degree of the node is [0|1]
root = root.lchild if root.lchild else root.rchild
return root
六、平衡搜索树
1、保证最坏情况下,搜索、插入和删除的操作的时间复杂度是O(logn)的搜索树算法:AVL树、伸展树、红黑树
2、平衡搜索树:某些操作系列会生成高度与n成比例的不平衡树,这种树的时间复杂度是O(n)。平衡搜索树是通过旋转操作调整不平衡树高度,使树避免非常不平衡的数结构。
3、平衡二叉搜索树的主要操作:旋转。第一步:修改位置两个位置父子关系;第二步:利用被旋转的两个位置之间的键连接子树节点。旋转之后二叉树键的结构特性保持不变!
4、单个旋转修改位置p的父子关系;双旋转是位置p在3个关联的键的中键时,第一次旋转到p的父节点上,第二次旋转到p祖父节点上;时间复杂度均为O(1)
5、trinode重组:在一棵树内部,将一个或多个旋转合并来提供更广泛的平衡的复合操作>>>4种可能,2种单旋转+2种双旋转;时间复杂度为O(1)
6、h+1≤n≤2h+1-1、h<2log(n(h))+2、
7、平衡操作的钩子,
8、平衡搜索树的“旋转”代码
def _relink(self, parent, child, make_left_child):
"""relink parent node with child node(allow child to be none"""
if make_left_child: # make it a left child
parent._left = child
else:
parent._right = child # make it a _right child
if child is not None: # make child to parent
child._parent = parent
def _rotate(self, p):
"""rotate position p above its parent"""
x = p.__node
y = x.__parent
z = y.__parent
if z is None:
x.__parent = None # X becomes root
else:
self._relink(z, x, y == z.__left) # x becomes a direct child of z
# now rotate x and y,including transfer of middle subtree
if x == y.__left:
self._relink(y, x.__left, True) # x.__left becomes left child of y
self._relink(x, y, False) # y becomes right child of x
else:
self._relink(y, x.__left, False) # x.__left becomes right child of y
self._relink(x, y, True) # y becomes left child of x
def _restructure(self, x):
"""perform trinode restructure of position x with parent/grandparent"""
y = self.parent(x)
z = self.parent(y)
if (x == self.right(y)) == (y == self.right(z)): # matching alignments
self._rotate(y) # single rotation (of y)
return y # y is new subtree root
else:
self._rotate(x) # opposite alignments
self._rotate(x) # double rotation(of x)
return x # x is new subtree root