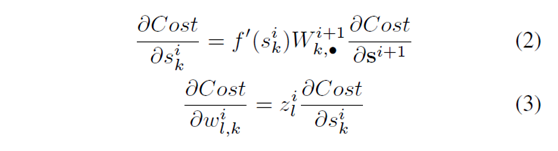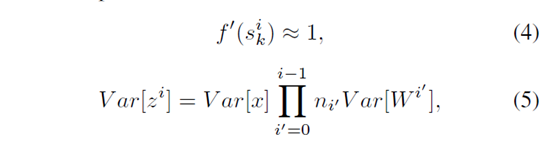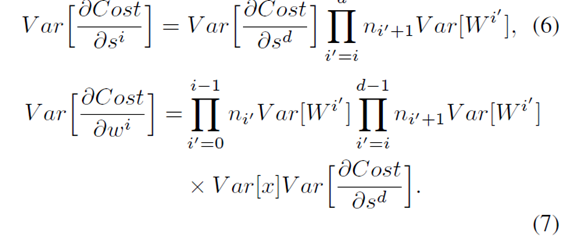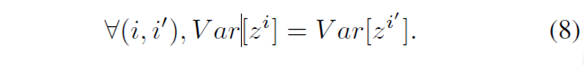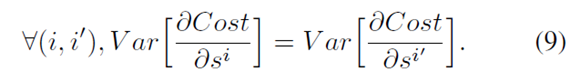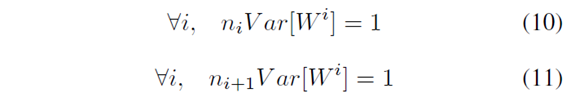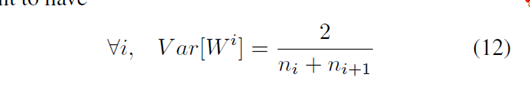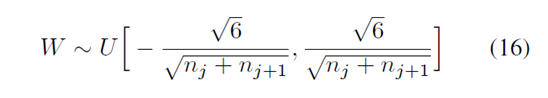本文作者为:Xavier Glorot与Yoshua Bengio。
本文干了点什么呢? 第一步:探索了不同的激活函数对网络的影响(包括:sigmoid函数,双曲正切函数和softsign y = x/(1+|x|) 函数)。
文中通过不断的实验:1,来monitor网络中隐藏单元的激活值来观察它的饱和性;2. 梯度。 并且evaluate 所选择的激活函数与初始化方法(预训练被看作一种特殊的初始化方法)。
实验数据的选择:
无穷多的训练集:ShapeSet-3*2: 它这个数据3集上进行在线学习,它的数据的大小是无穷多的,因为为不断地随机生成。在线学习(或不断学习)具有优点的:它可以把我们的任务focus在最优化问题上而不是小样本中回归问题,明白吧,应该。 还应该指出:当面对很大很大的训练集时,从非监督学习预训练中来进行初始化网络仍然使网络的性能有巨大的提升,意思就是当面对在的训练集时,非监督学习预训练的作用依然没有消失。
这是一个人工生成的数据集:每一个样本中包括2个形状(从三角形,长方形与椭圆形中选择),并且它们的大小、角度等参数都是任意的,唯一的限制为一方不能覆盖另一方50%即可。 所以最终会有9种结果。这个任务是相当难的:第一,我们的分类结果要对样本对象的角度、大小、平移等具有不变性;第二:同时需要学习专门变量的参数来识别三角目标对样本进行预测。
有限多的训练集: MNIST digits ,10个数字的识别,50000个用于训练,10000用于 validation,10000个用于测试。
CIFAR-10 :10种物品的识别,40000个用于训练,10000用于 validation,10000个用于测试。
Small-ImageNet:10个物品的识别,90000个用于训练,10000用于 validation,10000个用于测试。
实验的设置:
实验设置基本没有什么技巧,因为也还是文章的目的所在。
网络的隐含层选择1-5层,每一层的网络的神经单元数为1000个,输出层为一个softmax logistic regression。 代价函数为:negtive log-likelihood,即:-log P(y|x).
网络的优化方法为:梯度的反向传播算法, mini-batches的大小为10。权值更新过程中的学习率基于验证集误差来确定。
在隐含层选用分别试验三种不同的激活函数:sigmoid函数, 双曲正切函数, softsign函数,后面两个函数的是相似的,唯一的区别在于:双曲正切函数以指数型接近渐近线(速度快),softsign函数以二次型接近它的渐近线。
网络权值的确定为下面区间上的均匀分布,其中 n 为:前一层的单元数。
不同的激活函数对网络的影响:
在选择激活函数时,我们总要去避免两点:第一点,避免激活函数的过饱和(因为这样的话,梯度就不会很好地在网络中传播),第二点,过度线性化(由于激活函数没有了非线性,那么,它学习到的东西会变少,非线性才可以拟合更多)。
sigmoid激活函数:
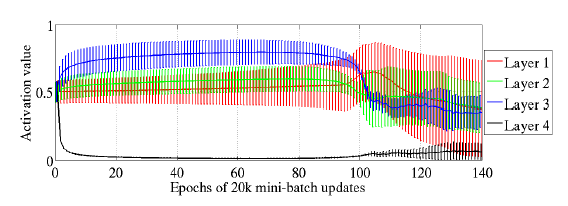
对于sigmoid激活函数问题,LeCun(1998b)已经研究过了,它会降低学习速率的(由于它的mean不是0)。文章中,这里选择sigmoid激活函数的目的是来通过观察它的激活值来反应的它的饱和程度。下图为实验的结果:
先说一句,上面的网络为4层的隐含层,我们通过上面的图可以看出:第一层至第三层的隐含层的输出的mean基本为0.5左右,对于sigmoid函数来说,在0.5附近的话,它不是饱和区的,是线性区的, 而第四层呢?它的输出的平均值随着迭代迅速下降至0左右,进入了饱和区了。然后,到后面的话,随着迭代不断进行,又稍微慢慢的有跳出饱和区的倾向。
文中解释的原因为:由于权值一开始是随机初始化的,所以呢,前面几层的输出对于最后输出的各类的预测是基本没有作用的,或者说直到第三层为止,前几层的输出都是随机的,而第四层的输出加权后的值直接影响到的最后的代价函数的,因为它后面接的是softmax的输出层的,即,第四层的 b+Wh 值关系到输出层的预测。而 h 为第四层的输出。 为了在一开始让 h 的值不至于影响到 b+Wh 值,网络自己就在代价函数的作用下学习了,学习的结果就是:h的结果驱于0了,偏置b 学习迅速,支撑起了整个预测结果。(我这里有一个疑问:为什么不是让w学习得到的值为0呢?如果第四层的包含层的输出为0了,是由于第三层与第四层相连的权值导致的,对吧,权值的变化是学习得到的,第四层与输出层的权值什么时候都可以学习到的,因为它们不经过激活函数的,为什么不直接把这个权值w变为0呢,为什么要去学习前一层的权值?我觉得在必要去跟综可能权值的变化看看分析的过程是否正确呢?总之吧,这个权值的学习是很随机的的应该,或者说很难去预测的)。在这里说明一下:对于第四层的激活值迅速变为0,会使得sigmoid的激活函数进入饱和区的,对于双曲正切与softsign激活函数来说则不会进入饱和区的,对吧)。
双曲正切激活函数与softsign激活函数:
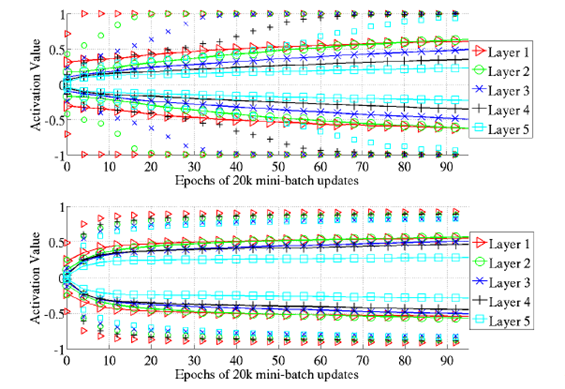
实验观察到的结果为:
我们会发现,从第一层开始至第五层,逐渐每层慢慢进行饱和区了。对于这个现象,文中也没有给出合理的推测。
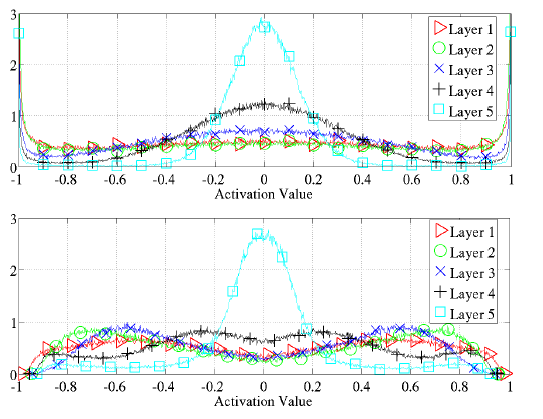
再看看双曲正切激活函数与softsign激活函数的 区别吧,下面的的图为训练完成以后的结果激活值的分布图:
从上图看,softsign激活函数的结果会更好一些,因为吧,一二三四层的激活值的分布基本在0.4-0.8之间,没有过饱和,同样也没有过线性(在0.5处会线性的);而双曲正切激活函数的话,对于第一至四层的话,很多值分布在-1或1附近,这肯定是饱和状态了吧。
网络的梯度与在网络中的传播
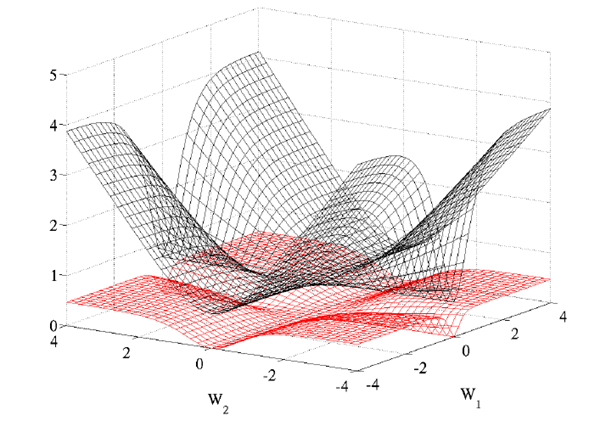
不同代价函数的影响:在1986年 Rumelhart 已经发现:logistic function 或者叫 conditional log-likelihood function: -log P(y|x) 的效果比 quadratic cost function的效果好很多的,原因在于 quadratic cost function在训练过程中会出现更多的 plateaus。文章给出了一个两个参数下的图:
初始化的梯度分析:
文中基于Bradley(2009)的理论分析 the variance of the back-propagated gradients,并提出一种新的权值初始化的方法。
分析的前提:1. 网络在初始化处于线性条件下,即激活活函数的导数为1;2. 初始化的权值的mean 为0,且独立同分布的;3, 输入特征 x 的 variance是相同的。经过一系列推导,得到了下面这样的结果:(文中的推导过程我也推了一遍,有的地方与文中有所不同,不过大致是相同的,并且不影响结果)
第一:
第二:公式5有用哦:
第三:公式6有用;
推出这玩意来了以后呢, 下面是关键:
1.前向传播:用文中的话说:From a forward-propagation point of view, to keep information flowing we would like that:
就是说,为了在前向传播过程中,可以让信息向前传播,做法就是让:激活单元的输出值的方差持不变。为什么要这样呢??有点小不理解。。
2. 反向传播:在反向传播过程中,也是为了让梯度可以反向传播,让:对激活单元输入值的梯度 保持不变,即:
最后得到的结论就是:
上面两个式子折衷一下,为:
所以呢,权值初始化时,服从这样的分布:
这个方法就叫做: normalized initialization.
在训练过程中,梯度问题:
这时,我们就不能单纯地用梯度的 variance 去分析了,因为已经不满足我们的假设条件了啊。
文章后面的一大堆基本没有什么重点的东西了吧,我觉得。写几个觉得有必要的总结吧:
1. softsign激活函数与双曲正切函数相比,效果还 很不错的,
2. normalized initialization 的方法很不错。
3. 在训练过程中,monitor 激活值与梯度的在不同层之间的变化是很好的分析工具。